Hostname: page-component-cd9895bd7-dzt6s Total loading time: 0 Render date: 2024-12-23T16:53:52.324Z Has data issue: false hasContentIssue false
  • English
  • Français

COMPUTABLE POLISH GROUP ACTIONS

Published online by Cambridge University Press:  01 August 2018

ALEXANDER MELNIKOV  and
ANTONIO MONTALBÁN
ALEXANDER MELNIKOV
Affiliation:
THE INSTITUTE OF NATURAL AND MATHEMATICAL SCIENCES MASSEY UNIVERSITY AUCKLAND, NEW ZEALANDE-mail:alexander.g.melnikov@gmail.com
ANTONIO MONTALBÁN
Affiliation:
DEPARTMENT OF MATHEMATICS UNIVERSITY OF CALIFORNIA BERKELEY, CA, USAE-mail:antonio@math.berkeley.eduURL: www.math.berkeley.edu/∼antonio
Get access Rights & Permissions [Opens in a new window]

Abstract

Using methods from computable analysis, we establish a new connection between two seemingly distant areas of logic: computable structure theory and invariant descriptive set theory. We extend several fundamental results of computable structure theory to the more general setting of topological group actions. As we will see, the usual action of 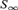${S_\infty }$ on the space of structures in a given language is effective in a certain algorithmic sense that we need, and 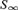${S_\infty }$ itself carries a natural computability structure (to be defined). Among other results, we give a sufficient condition for an orbit under effective 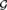${\cal G}$-action of a computable Polish 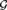${\cal G}$ to split into infinitely many disjoint effective orbits. Our results are not only more general than the respective results in computable structure theory, but they also tend to have proofs different from (and sometimes simpler than) the previously known proofs of the respective prototype results.

Keywords

03D9903C5703D45computable analysiscomputable algebradescriptive set theorytopological group actions
Type
Articles
Information
The Journal of Symbolic Logic , Volume 83 , Issue 2 , June 2018 , pp. 443 - 460
Copyright
Copyright © The Association for Symbolic Logic 2018 

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

Brattka, V., Hertling, P., and Weihrauch, K., A tutorial on computable analysis, New Computational Paradigms (Cooper, S. B., Löwe, B., and Sorbi, A., editors), Springer, New York, 2008, pp. 425–491.CrossRefGoogle Scholar
Effros, E. G., Transformation groups and ${C^{\rm{*}}}$-algebras. Annals of Mathematics, vol. 81 (1965), no. 2, pp. 38–55.CrossRefGoogle Scholar
Ershov, Y. L. and Goncharov, S. S., Constructive Models, Siberian School of Algebra and Logic, Consultants Bureau, New York, 2000.CrossRefGoogle Scholar
Gao, S., Invariant Descriptive Set Theory, Pure and Applied Mathematics (Boca Raton), vol. 293, CRC Press, Boca Raton, FL, 2009.Google Scholar
Gončarov, S. S., Selfstability, and computable families of constructivizations. Algebra i Logika, vol. 14 (1975), no. 6, pp. 647–680, 727.Google Scholar
Lopez-Escobar, E. G. K., An interpolation theorem for denumerably long formulas. Fundamenta Mathematicae, vol. 57 (1965), pp. 253–272.CrossRefGoogle Scholar
Martin, D. A., Classes of recursively enumerable sets and degrees of unsolvability. Zeitschrift für mathematische Logik und Grundlagen der Mathematik, vol. 12 (1966), pp. 295–310.CrossRefGoogle Scholar
Montalbán, A., A robuster scott rank. Proceedings of the American Mathematical Society, vol. 143 (2015), no. 12, pp. 5427–5436.CrossRefGoogle Scholar
Ventsov, Y. G., The effective choice problem for relations and reducibilities in classes of constructive and positive models. Algebra i Logika, vol. 31 (1992), no. 2, pp. 101–118, 220.Google Scholar
Weihrauch, K., On computable metric spaces Tietze-Urysohn extension is computable, Computability and Complexity in Analysis (Swansea, 2000) (Blanck, J., Brattka, V., and Hertling, P., editors), Lecture Notes in Computer Science, vol. 2064, Springer, Berlin, 2001, pp. 357–368.CrossRefGoogle Scholar
Weihrauch, K. and Grubba, T., Elementary computable topology. Journal of Universal Computer Science, vol. 15 (2009), no. 6, pp. 1381–1422.Google Scholar