Article contents
NUMBER SYSTEMS WITH SIMPLICITY HIERARCHIES: A GENERALIZATION OF CONWAY’S THEORY OF SURREAL NUMBERS II
Published online by Cambridge University Press: 05 February 2018
Abstract
In [16], the algebraico-tree-theoretic simplicity hierarchical structure of J. H. Conway’s ordered field 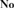 ${\bf{No}}$ of surreal numbers was brought to the fore and employed to provide necessary and sufficient conditions for an ordered field to be isomorphic to an initial subfield of
${\bf{No}}$ of surreal numbers was brought to the fore and employed to provide necessary and sufficient conditions for an ordered field to be isomorphic to an initial subfield of 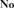 ${\bf{No}}$, i.e., a subfield of
${\bf{No}}$, i.e., a subfield of 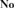 ${\bf{No}}$ that is an initial subtree of
${\bf{No}}$ that is an initial subtree of  ${\bf{No}}$. In this sequel to [16], analogous results for ordered abelian groups and ordered domains are established which in turn are employed to characterize the convex subgroups and convex subdomains of initial subfields of
${\bf{No}}$. In this sequel to [16], analogous results for ordered abelian groups and ordered domains are established which in turn are employed to characterize the convex subgroups and convex subdomains of initial subfields of 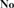 ${\bf{No}}$ that are themselves initial. It is further shown that an initial subdomain of
${\bf{No}}$ that are themselves initial. It is further shown that an initial subdomain of 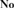 ${\bf{No}}$ is discrete if and only if it is a subdomain of
${\bf{No}}$ is discrete if and only if it is a subdomain of 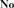 ${\bf{No}}$’s canonical integer part
${\bf{No}}$’s canonical integer part 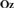 ${\bf{Oz}}$ of omnific integers. Finally, making use of class models the results of [16] are extended by showing that the theories of nontrivial divisible ordered abelian groups and real-closed ordered fields are the sole theories of nontrivial densely ordered abelian groups and ordered fields all of whose models are isomorphic to initial subgroups and initial subfields of
${\bf{Oz}}$ of omnific integers. Finally, making use of class models the results of [16] are extended by showing that the theories of nontrivial divisible ordered abelian groups and real-closed ordered fields are the sole theories of nontrivial densely ordered abelian groups and ordered fields all of whose models are isomorphic to initial subgroups and initial subfields of 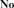 ${\bf{No}}$.
${\bf{No}}$.
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 3
- Cited by




