Article contents
CONSERVATIVITY OF ULTRAFILTERS OVER SUBSYSTEMS OF SECOND ORDER ARITHMETIC
Published online by Cambridge University Press: 01 August 2018
Abstract
We extend the usual language of second order arithmetic to one in which we can discuss an ultrafilter over of the sets of a given model. The semantics are based on fixing a subclass of the sets in a structure for the basic language that corresponds to the intended ultrafilter. In this language we state axioms that express the notion that the subclass is an ultrafilter and additional ones that say it is idempotent or Ramsey. The axioms for idempotent ultrafilters prove, for example, Hindman’s theorem and its generalizations such as the Galvin--Glazer theorem and iterated versions of these theorems (IHT and IGG). We prove that adding these axioms to IHT produce conservative extensions of ACA0 +IHT, 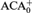 ${\rm{ACA}}_{\rm{0}}^ +$, ATR0,
${\rm{ACA}}_{\rm{0}}^ +$, ATR0, 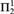 ${\rm{\Pi }}_2^1$-CA0, and
${\rm{\Pi }}_2^1$-CA0, and 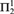 ${\rm{\Pi }}_2^1$-CA0 for all sentences of second order arithmetic and for full Z2 for the class of
${\rm{\Pi }}_2^1$-CA0 for all sentences of second order arithmetic and for full Z2 for the class of 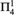 ${\rm{\Pi }}_4^1$ sentences. We also generalize and strengthen a metamathematical result of Wang (1984) to show, for example, that any
${\rm{\Pi }}_4^1$ sentences. We also generalize and strengthen a metamathematical result of Wang (1984) to show, for example, that any 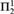 ${\rm{\Pi }}_2^1$ theorem ∀X∃YΘ(X,Y) provable in ACA0 or
${\rm{\Pi }}_2^1$ theorem ∀X∃YΘ(X,Y) provable in ACA0 or 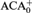 ${\rm{ACA}}_{\rm{0}}^ +$ there are e,k ∈ ℕ such that ACA0 or
${\rm{ACA}}_{\rm{0}}^ +$ there are e,k ∈ ℕ such that ACA0 or 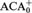 ${\rm{ACA}}_{\rm{0}}^ +$ proves that ∀X(Θ(X, Φe(J(k)(X))) where Φe is the eth Turing reduction and J(k) is the kth iterate of the Turing or Arithmetic jump, respectively. (A similar result is derived for
${\rm{ACA}}_{\rm{0}}^ +$ proves that ∀X(Θ(X, Φe(J(k)(X))) where Φe is the eth Turing reduction and J(k) is the kth iterate of the Turing or Arithmetic jump, respectively. (A similar result is derived for 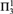 ${\rm{\Pi }}_3^1$ theorems of
${\rm{\Pi }}_3^1$ theorems of 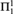 ${\rm{\Pi }}_1^1$-CA0 and the hyperjump.)
${\rm{\Pi }}_1^1$-CA0 and the hyperjump.)
Keywords
- Type
- Articles
- Information
- Copyright
- Copyright © The Association for Symbolic Logic 2018
References
REFERENCES
- 1
- Cited by




