Research Article
Codable sets and orbits of computably enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-28
-
- Article
- Export citation
Orthogonal families of real sequences
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 29-49
-
- Article
- Export citation
More on an undecidability result of Bateman, Jockusch and Woods
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 50
-
- Article
- Export citation
Small forcing makes any cardinal superdestructible
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 51-58
-
- Article
- Export citation
Models of arithmetic and subuniform bounds for the arithmetic sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 59-72
-
- Article
- Export citation
On the expressiveness of frame satisfiability and fragments of second-order logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 73-82
-
- Article
- Export citation
One-dimensional fibers of rigid subanalytic sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 83-88
-
- Article
- Export citation
Supplements of bounded permutation groups
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 89-102
-
- Article
- Export citation
Uniformization and skolem functions in the class of trees
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 103-127
-
- Article
- Export citation
Ideals without ccc
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 128-148
-
- Article
- Export citation
Laver indestructibility and the class of compact cardinals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 149-157
-
- Article
- Export citation
Generic saturation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 158-162
-
- Article
- Export citation
Relativised quantification: Some canonical varieties of sequence-set algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 163-184
-
- Article
- Export citation
On effective topological spaces
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 185-221
-
- Article
- Export citation
Pseudo-superstructures as nonstandard universes
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 222-236
-
- Article
- Export citation
Undecidable wreath products and skew power series fields
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 237-246
-
- Article
- Export citation
Extensional quotients for type theory and the consistency problem for NF
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 247-261
-
- Article
- Export citation
Vanishing Borel sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 262-268
-
- Article
- Export citation
Propositional quantification in the monadic fragment of intuitionistic logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 269-300
-
- Article
- Export citation
The algebraic sum of sets of real numbers with strong measure zero sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 301-324
-
- Article
- Export citation



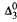 -automorphism method we introduced earlier.
-automorphism method we introduced earlier.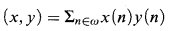
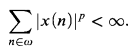
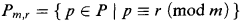
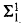 (Ackermann) and
(Ackermann) and 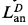 (see [5] and [6]) is
(see [5] and [6]) is 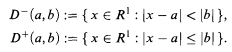
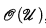 , are defined inductively as follows.
, are defined inductively as follows. 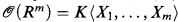 , the ring of strictly convergent power series in
, the ring of strictly convergent power series in 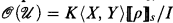 , (where
, (where 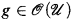 have no common zero on
have no common zero on 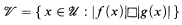
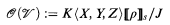
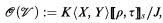
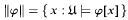
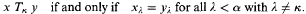
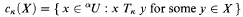
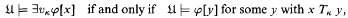
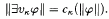
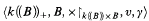
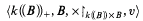
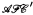 is a set in
is a set in 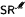 -sets. They also characterize the property (*) introduced by Gerlits and Nagy in terms of older concepts.
-sets. They also characterize the property (*) introduced by Gerlits and Nagy in terms of older concepts.