Article contents
One-dimensional fibers of rigid subanalytic sets
Published online by Cambridge University Press: 12 March 2014
Extract
Let K be an algebraically closed field of any characteristic, complete with respect to the non-trivial ultrametric absolute value ∣·∣: K → ℝ+. By R denote the valuation ring of K, and by ℘ its maximal ideal. We work within the class of subanalytic sets defined in [5], but our results here also hold for the strongly subanalytic sets introduced in [11] as well as for those subanalytic sets considered in [6]. Let X ⊂ R1 be subanalytic. In [8], we showed that there is a decomposition of X as a union of a finite number of special sets U ⊂ R1 (see below). In this note, in Theorem 1.6, we obtain a version of this result which is uniform in parameters, thereby answering a question brought to our attention by Angus Macintyre. It follows immediately from Theorem 1.6 that the theory of K in the language 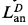 (see [5] and [6]) is C-minimal in the sense of [3] and [9]. The analogous uniformity result in the p-adic case was recently proved in [12].
(see [5] and [6]) is C-minimal in the sense of [3] and [9]. The analogous uniformity result in the p-adic case was recently proved in [12].
Definition 1.1. (i) A disc in R1 is a set of one of the two following forms:
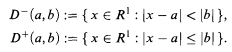
A special set in R1 is a disc minus a finite union of discs.
(ii) R-domains u ⊂ Rm, and their associated rings of analytic functions, 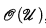 , are defined inductively as follows. Rm is an R-domain and
, are defined inductively as follows. Rm is an R-domain and 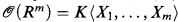 , the ring of strictly convergent power series in X1,…, Xm over K. If u is an R-domain with associated ring
, the ring of strictly convergent power series in X1,…, Xm over K. If u is an R-domain with associated ring 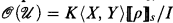 , (where K 〈X, Y〉 〚ρ〛S is a ring of separated power series, see [5, §2] and [1, §1]) and f,
, (where K 〈X, Y〉 〚ρ〛S is a ring of separated power series, see [5, §2] and [1, §1]) and f, 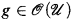 have no common zero on u and ◸ ϵ {<, ≤}, then
have no common zero on u and ◸ ϵ {<, ≤}, then
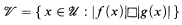
is an R-domain and
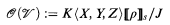
where J is the ideal generated by I and f − gZ (Z is a new variable) if ◸ is ≤, and
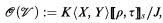
where J is the ideal generated by I and f − gτ (τ a new variable) if ◸ is <. (See [8, Definition 2.2].) R-domains generalize the rational domains of [2, §7.2.3]. It is true, but not easy to prove, that 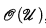 only depends on u as a point set, and is independent of the particular representation of u.
only depends on u as a point set, and is independent of the particular representation of u.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998
References
REFERENCES
- 18
- Cited by




