No CrossRef data available.
Article contents
Orthogonal families of real sequences
Published online by Cambridge University Press: 12 March 2014
Extract
For x, y ϵ ℝω define the inner product
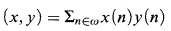
which may not be finite or even exist. We say that x and y are orthogonal if (x, y) converges and equals 0.
Define lp to be the set of all x ϵ ℝω such that
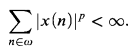
For Hilbert space, l2, any family of pairwise orthogonal sequences must be countable. For a good introduction to Hilbert space, see Retherford [4].
Theorem 1. There exists a pairwise orthogonal family F of size continuum such that F is a subset of lp for every p > 2.
It was already known that there exists a family of continuum many pairwise orthogonal elements of ℝω. A family F ⊆ ℝω∖0 of pairwise orthogonal sequences is orthogonally complete or a maximal orthogonal family iff the only element of ℝω orthogonal to every element of F is 0, the constant 0 sequence.
It is somewhat surprising that Kunen's perfect set of orthogonal elements is maximal (a fact first asserted by Abian). MAD families, nonprincipal ultrafilters, and many other such maximal objects cannot be even Borel.
Theorem 2. There exists a perfect maximal orthogonal family of elements of ℝω.
Abian raised the question of what are the possible cardinalities of maximal orthogonal families.
Theorem 3. In the Cohen real model there is a maximal orthogonal set in ℝω of cardinality ω1, but there is no maximal orthogonal set of cardinality κ with ω1 < κ < ϲ.
By the Cohen real model we mean any model obtained by forcing with finite partial functions from γ to 2, where the ground model satisfies GCH and γω = γ.
- Type
- Research Article
- Information
- Copyright
- Copyright © Association for Symbolic Logic 1998




