Research Article
The effective content of surreal algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 337-371
-
- Article
- Export citation
The cylindric algebras of three-valued logic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1201-1217
-
- Article
- Export citation
Higher gap morasses, Ia: Gap-two morasses and condensation
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 753-787
-
- Article
- Export citation
Codable sets and orbits of computably enumerable sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1-28
-
- Article
- Export citation
Relative constructivity
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1218-1238
-
- Article
- Export citation
Definability and definable groups in simple theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 788-796
-
- Article
- Export citation
Orthogonal families of real sequences
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 29-49
-
- Article
- Export citation
Definability and descent
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 372-378
-
- Article
- Export citation
Filtral powers of structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1239-1254
-
- Article
- Export citation
Undecidable extensions of Skolem arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 379-401
-
- Article
- Export citation
More on an undecidability result of Bateman, Jockusch and Woods
-
- Published online by Cambridge University Press:
- 12 March 2014, p. 50
-
- Article
- Export citation
Σ2 Induction and infinite injury priority argument, Part I: Maximal sets and the jump operator
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 797-814
-
- Article
- Export citation
Automorphisms moving all non-algebraic points and an application to NF
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 815-830
-
- Article
- Export citation
Small forcing makes any cardinal superdestructible
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 51-58
-
- Article
- Export citation
Solving Pell equations locally in models of IΔ0
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 402-410
-
- Article
- Export citation
Equivalence elementaire et decidabilite pour des structures du type groupe agissant sur un groupe abelien
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1255-1285
-
- Article
- Export citation
Relative enumerability in the difference hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 411-420
-
- Article
- Export citation
Multiplicative conjunction and an algebraic meaning of contraction and weakening
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 831-859
-
- Article
- Export citation
Models of arithmetic and subuniform bounds for the arithmetic sets
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 59-72
-
- Article
- Export citation
Termination and confluence in infinitary term rewriting
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 1286-1296
-
- Article
- Export citation

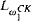 . This equivalence is used to answer several open questions concerning the metadyadics. Results obtained seem to indicate that the metadyadics best capture the notion of a recursive surreal number.
. This equivalence is used to answer several open questions concerning the metadyadics. Results obtained seem to indicate that the metadyadics best capture the notion of a recursive surreal number.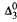 -automorphism method we introduced earlier.
-automorphism method we introduced earlier.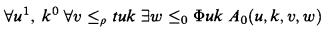
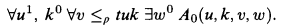
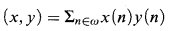
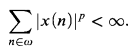
 arithmetical statement about the syntax of first order logic ([6, §3])).
arithmetical statement about the syntax of first order logic ([6, §3])). be an elementary class closed under updirected unions (e.g., if
be an elementary class closed under updirected unions (e.g., if 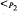 be the restriction of usual order relation to integers which are primes or squares of primes, and let ⊥ denote the coprimeness predicate. The elementary theory of
be the restriction of usual order relation to integers which are primes or squares of primes, and let ⊥ denote the coprimeness predicate. The elementary theory of 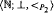 is undecidable. Now denote by <π the restriction of order to primary numbers. All arithmetical relations restricted to primary numbers are definable in the structure (ℕ; ⊥, <π). Furthermore, the structures (ℕ; ∣, <π) (ℕ; =, ×, <π) and (ℕ; =, +, ×) are interdefinable.
is undecidable. Now denote by <π the restriction of order to primary numbers. All arithmetical relations restricted to primary numbers are definable in the structure (ℕ; ⊥, <π). Furthermore, the structures (ℕ; ∣, <π) (ℕ; =, ×, <π) and (ℕ; =, +, ×) are interdefinable.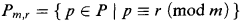
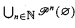 .
.