Hostname: page-component-76fb5796d-zzh7m Total loading time: 0 Render date: 2024-04-25T12:56:01.503Z Has data issue: false hasContentIssue false
  • English
  • Français

Undecidable extensions of Skolem arithmetic

Published online by Cambridge University Press:  12 March 2014

Alexis Bès  and
Denis Richard
Alexis Bès
Affiliation:
Equipe de Logique, Université Paris 7, 2, Place Jussieu, 75251 Paris Cedex 05, France, E-mail: bes@logique.jussieu.fr
Denis Richard
Affiliation:
Laboratoire de Logique, Algorithmique, et Informatique de Clermont I (LLAIC 1), I. U. T. Informatique, B. P. 86, F-63172 Aubière Cedex, France, E-mail: richard@llaic.u-clermontl.fr
Get access Rights & Permissions [Opens in a new window]

Abstract

Let 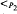be the restriction of usual order relation to integers which are primes or squares of primes, and let ⊥ denote the coprimeness predicate. The elementary theory of 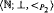is undecidable. Now denote by <π the restriction of order to primary numbers. All arithmetical relations restricted to primary numbers are definable in the structure (ℕ; ⊥, <π). Furthermore, the structures (ℕ; ∣, <π) (ℕ; =, ×, <π) and (ℕ; =, +, ×) are interdefinable.

Résumé

Résumé

Soit 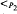la restriction de l'ordre usuel aux entiers qui sont premiers ou carrés de premiers, et soit ⊥ le prédicat de coprimarité. La théorie élémentaire de 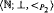est indécidable. Soit maintenant <π l'ordre restreint aux entiers primaires. Toute relation arithmétique restreinte aux entiers primaires est définissable dans la structure (ℕ; ⊥, <π). De plus, les structures (ℕ; ∣, <π) (ℕ; =, ×, <π) et (ℕ; =, +, ×) sont inter-définissables.

Type
Research Article
Information
The Journal of Symbolic Logic , Volume 63 , Issue 2 , June 1998 , pp. 379 - 401
Copyright
Copyright © Association for Symbolic Logic 1998

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

References

REFERENCES

[1] Cegielski, P., Matiyasevich, Y., and Richard, D., Definability and decidability issues in extensions of the integers with the divisibility predicate, this Journal, vol. 61 (1996), no. 2, pp. 515–540.Google Scholar
[2] Ellison, W. J. and Mendès-France, M., Les nombres premiers, Ed. Hermann, , Paris, 1975.Google Scholar
[3] Maurin, F., The theory of integer multiplication with order restricted to primes is decidable, this Journal, vol. 62 (1997), no. 1, pp. 123–130.Google Scholar
[4] Putnam, H., Decidability and essential undecidability, this Journal, vol. 22 (1957), pp. 39–54.Google Scholar
[5] Richard, D., All arithmetical sets of powers of primes are first-order definable in terms of the successor function and the coprimeness predicate, Discrete Mathematics, vol. 53 (1985), pp. 221–247.Google Scholar
[6] Robinson, J., Definability and decision problems in arithmetic, this Journal, vol. 14 (1949), pp. 98–114.Google Scholar
[7] Skolem, T., über gewisse Satzfunktionen in der Arithmetik, Skr. Norske Videnskaps-Akademie i Oslo, vol. 7 (1930).Google Scholar
[8] Woods, A. R., Some problems in logic and number theory and their connections, Ph.D. thesis , University of Manchester, 1981.Google Scholar