Research Article
The effective content of surreal algebra
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 337-371
-
- Article
- Export citation
Definability and descent
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 372-378
-
- Article
- Export citation
Undecidable extensions of Skolem arithmetic
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 379-401
-
- Article
- Export citation
Solving Pell equations locally in models of IΔ0
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 402-410
-
- Article
- Export citation
Relative enumerability in the difference hierarchy
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 411-420
-
- Article
- Export citation
On minimal structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 421-426
-
- Article
- Export citation
DOP and FCP in generic structures
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 427-438
-
- Article
- Export citation
The representation theories of elementarily equivalent rings
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 439-450
-
- Article
- Export citation
The logic of recursive equations
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 451-478
-
- Article
- Export citation
Amalgamation in relation algebras
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 479-484
-
- Article
- Export citation
There are
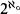 many almost strongly minimal generalized n-gons that do not interpret an infinite group
many almost strongly minimal generalized n-gons that do not interpret an infinite group
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 485-508
-
- Article
- Export citation
Explicit mathematics with the monotone fixed point principle
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 509-542
-
- Article
- Export citation
Some two-cardinal results for O-minimal theories
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 543-548
-
- Article
- Export citation
Superdestructibility: A dual to Laver's indestructibility
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 549-554
-
- Article
- Export citation
A strong version of Herbrand's theorem for introvert sentences
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 555-569
-
- Article
- Export citation
Paires de structures O-minimales
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 570-578
-
- Article
- Export citation
Sequentially continuous linear mappings in constructive analysis
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 579-583
-
- Article
- Export citation
The Rudin-Blass ordering of ultrafilters
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 584-592
-
- Article
- Export citation
Changing cardinal invariants of the reals without changing cardinals or the reals
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 593-599
-
- Article
- Export citation
On the computational content of the axiom of choice
-
- Published online by Cambridge University Press:
- 12 March 2014, pp. 600-622
-
- Article
- Export citation

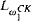 . This equivalence is used to answer several open questions concerning the metadyadics. Results obtained seem to indicate that the metadyadics best capture the notion of a recursive surreal number.
. This equivalence is used to answer several open questions concerning the metadyadics. Results obtained seem to indicate that the metadyadics best capture the notion of a recursive surreal number.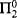 arithmetical statement about the syntax of first order logic ([6, §3])).
arithmetical statement about the syntax of first order logic ([6, §3])).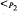 be the restriction of usual order relation to integers which are primes or squares of primes, and let ⊥ denote the coprimeness predicate. The elementary theory of
be the restriction of usual order relation to integers which are primes or squares of primes, and let ⊥ denote the coprimeness predicate. The elementary theory of 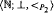 is undecidable. Now denote by <π the restriction of order to primary numbers. All arithmetical relations restricted to primary numbers are definable in the structure (ℕ; ⊥, <π). Furthermore, the structures (ℕ; ∣, <π) (ℕ; =, ×, <π) and (ℕ; =, +, ×) are interdefinable.
is undecidable. Now denote by <π the restriction of order to primary numbers. All arithmetical relations restricted to primary numbers are definable in the structure (ℕ; ⊥, <π). Furthermore, the structures (ℕ; ∣, <π) (ℕ; =, ×, <π) and (ℕ; =, +, ×) are interdefinable.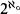 many almost strongly minimal generalized
many almost strongly minimal generalized 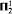 comprehension.
comprehension.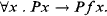
 and
and  from a regular
from a regular