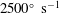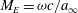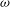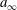Focus on Fluids
Taylor vortices versus Taylor columns
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
A numerical study of the dynamics of a particle settling at moderate Reynolds numbers in a linearly stratified fluid
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 5-32
-
- Article
- Export citation
Applicability and failure of the flux-gradient laws in double-diffusive convection
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 33-72
-
- Article
- Export citation
Experimental investigation of flow behind a cube for moderate Reynolds numbers
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 73-98
-
- Article
- Export citation
The high-Reynolds-number asymptotic development of nonlinear equilibrium states in plane Couette flow
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 99-112
-
- Article
- Export citation
Generating controllable velocity fluctuations using twin oscillating hydrofoils: experimental validation
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 113-123
-
- Article
- Export citation
Cloaking of a vertical cylinder in waves using variable bathymetry
-
- Published online by Cambridge University Press:
- 30 May 2014, pp. 124-143
-
- Article
- Export citation
The mechanism of shape instability for a vesicle in extensional flow
-
- Published online by Cambridge University Press:
- 02 June 2014, pp. 144-190
-
- Article
- Export citation
Numerical simulation of turbulent duct flows with constant power input
-
- Published online by Cambridge University Press:
- 02 June 2014, pp. 191-209
-
- Article
- Export citation
Two-dimensional planar plumes and fountains
-
- Published online by Cambridge University Press:
- 04 June 2014, pp. 210-244
-
- Article
- Export citation
Two-dimensional planar plumes: non-Boussinesq effects
-
- Published online by Cambridge University Press:
- 04 June 2014, pp. 245-258
-
- Article
- Export citation
Tidal flow over topography: effect of excursion number on wave energetics and turbulence
-
- Published online by Cambridge University Press:
- 09 June 2014, pp. 259-283
-
- Article
- Export citation
The role of conservative forces in rotor aerodynamics
-
- Published online by Cambridge University Press:
- 09 June 2014, pp. 284-315
-
- Article
- Export citation
Active control of a turbulent boundary layer based on local surface perturbation
-
- Published online by Cambridge University Press:
- 09 June 2014, pp. 316-354
-
- Article
- Export citation
Disruptive bubble behaviour leading to microstructure damage in an ultrasonic field
-
- Published online by Cambridge University Press:
- 09 June 2014, pp. 355-371
-
- Article
- Export citation
Interactions of large amplitude solitary waves in viscous fluid conduits
-
- Published online by Cambridge University Press:
- 11 June 2014, pp. 372-384
-
- Article
- Export citation
Dynamic transition from Mach to regular reflection of shock waves in a steady flow
-
- Published online by Cambridge University Press:
- 09 June 2014, pp. 385-400
-
- Article
- Export citation
Solitary waves on a ferrofluid jet
-
- Published online by Cambridge University Press:
- 09 June 2014, pp. 401-420
-
- Article
- Export citation
Hierarchical parcel-swapping representation of turbulent mixing. Part 2. Application to channel flow
-
- Published online by Cambridge University Press:
- 10 June 2014, pp. 421-463
-
- Article
- Export citation
Linear instability, nonlinear instability and ligament dynamics in three-dimensional laminar two-layer liquid–liquid flows
-
- Published online by Cambridge University Press:
- 10 June 2014, pp. 464-506
-
- Article
- Export citation