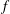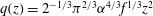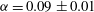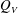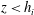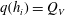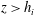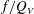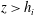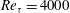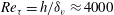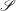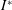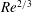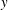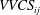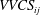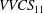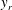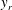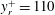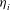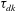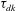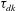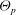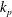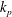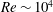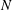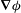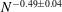Focus on Fluids
The surprising relevance of a continuum description to granular clusters
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 1-4
-
- Article
-
- You have access
- Export citation
Papers
Adding in-line motion and model-based optimization offers exceptional force control authority in flapping foils
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 5-34
-
- Article
- Export citation
Detrainment from a turbulent plume produced by a vertical line source of buoyancy in a confined, ventilated space
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 35-49
-
- Article
- Export citation
Stochastic dynamics of active swimmers in linear flows
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 50-70
-
- Article
- Export citation
Wavepacket models for supersonic jet noise
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 71-95
-
- Article
- Export citation
Erythrocyte responses in low-shear-rate flows: effects of non-biconcave stress-free state in the cytoskeleton
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 96-118
-
- Article
- Export citation
The turbulent/non-turbulent interface and entrainment in a boundary layer
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 119-151
-
- Article
- Export citation
Unsteady propulsion near a solid boundary
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 152-170
-
- Article
- Export citation
Velocity statistics in turbulent channel flow up to
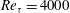 $Re_{\tau }=4000$
$Re_{\tau }=4000$
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 171-191
-
- Article
- Export citation
Turbulent wake behind a curved circular cylinder
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 192-229
-
- Article
- Export citation
A Kolmogorov-like exact relation for compressible polytropic turbulence
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 230-242
-
- Article
- Export citation
Coins falling in water
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 243-253
-
- Article
- Export citation
Transient growth in linearly stable Taylor–Couette flows
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 254-290
-
- Article
- Export citation
Velocity–vorticity correlation structure in turbulent channel flow
-
- Published online by Cambridge University Press:
- 24 February 2014, pp. 291-307
-
- Article
-
- You have access
- Open access
- Export citation
An experimental study of the free evolution of rotating, nonlinear internal gravity waves in a two-layer stratified fluid
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 308-339
-
- Article
- Export citation
Maximum palinstrophy growth in 2D incompressible flows
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 340-367
-
- Article
- Export citation
On multiphase turbulence models for collisional fluid–particle flows
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 368-424
-
- Article
- Export citation
Effect of a distant rigid wall on microstreaming generated by an acoustically driven gas bubble
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 425-445
-
- Article
- Export citation
Effects of magnetic field on the turbulent wake of a cylinder in free-surface magnetohydrodynamic channel flow
-
- Published online by Cambridge University Press:
- 25 February 2014, pp. 446-465
-
- Article
- Export citation
Effects of distributed pressure gradients on the pressure–strain correlations in a supersonic nozzle and diffuser
-
- Published online by Cambridge University Press:
- 21 February 2014, pp. 466-494
-
- Article
- Export citation