Vortex-induced vibration of a circular cylinder with low mass ratio (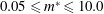 $0.05\leqslant m^{\ast }\leqslant 10.0$) is investigated, via a stabilized space–time finite element formulation, in the laminar flow regime where
$0.05\leqslant m^{\ast }\leqslant 10.0$) is investigated, via a stabilized space–time finite element formulation, in the laminar flow regime where 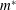 $m^{\ast }$ is defined as the ratio of the mass of the oscillating structure to the mass of the fluid displaced by it. Computations are carried out over a wide range of reduced speed,
$m^{\ast }$ is defined as the ratio of the mass of the oscillating structure to the mass of the fluid displaced by it. Computations are carried out over a wide range of reduced speed, 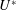 $U^{\ast }$, which is defined as
$U^{\ast }$, which is defined as 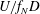 $U/f_{N}D$, where
$U/f_{N}D$, where 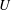 $U$ is the free-stream speed,
$U$ is the free-stream speed, 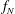 $f_{N}$ the natural frequency of the spring mass system in vacuum and
$f_{N}$ the natural frequency of the spring mass system in vacuum and 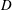 $D$ the diameter of the cylinder. In particular, the situation where the lock-in regime extends up to infinite reduced speed is explored. Studies at large
$D$ the diameter of the cylinder. In particular, the situation where the lock-in regime extends up to infinite reduced speed is explored. Studies at large 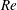 $Re$, in the past, have shown that the normalized amplitude of cylinder oscillation at infinite reduced speed,
$Re$, in the past, have shown that the normalized amplitude of cylinder oscillation at infinite reduced speed, 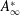 $A_{\infty }^{\ast }$, exhibits a sharp increase when
$A_{\infty }^{\ast }$, exhibits a sharp increase when 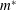 $m^{\ast }$ is reduced below the critical mass ratio (
$m^{\ast }$ is reduced below the critical mass ratio (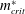 $m_{crit}^{\ast }$). This jump signifies a shift from desynchronized response to lock-in state. In this work it is shown that in the laminar regime, a jump in
$m_{crit}^{\ast }$). This jump signifies a shift from desynchronized response to lock-in state. In this work it is shown that in the laminar regime, a jump in 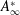 $A_{\infty }^{\ast }$ occurs only beyond a certain
$A_{\infty }^{\ast }$ occurs only beyond a certain 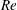 $Re$ (
$Re$ (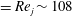 $=Re_{j}\sim 108$). For
$=Re_{j}\sim 108$). For 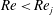 $Re<Re_{j}$, the response increases smoothly with decrease in
$Re<Re_{j}$, the response increases smoothly with decrease in 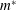 $m^{\ast }$ with no discernible jump. In this situation, therefore, the identification of
$m^{\ast }$ with no discernible jump. In this situation, therefore, the identification of 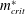 $m_{crit}^{\ast }$ based on jump in response at
$m_{crit}^{\ast }$ based on jump in response at 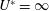 $U^{\ast }=\infty$ is not possible. The difference in the
$U^{\ast }=\infty$ is not possible. The difference in the 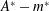 $A^{\ast }-m^{\ast }$ variation on the two sides of
$A^{\ast }-m^{\ast }$ variation on the two sides of 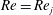 $Re=Re_{j}$, is attributed to the difference in the transition between the lower branch of cylinder response and desynchronization regime. This transition is brought out more clearly by plotting
$Re=Re_{j}$, is attributed to the difference in the transition between the lower branch of cylinder response and desynchronization regime. This transition is brought out more clearly by plotting 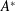 $A^{\ast }$ with
$A^{\ast }$ with 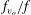 $f_{v_{o}}/f$, where
$f_{v_{o}}/f$, where 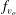 $f_{v_{o}}$ is the vortex shedding frequency for the flow past a stationary cylinder and
$f_{v_{o}}$ is the vortex shedding frequency for the flow past a stationary cylinder and 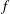 $f$ is the cylinder vibration frequency. In the
$f$ is the cylinder vibration frequency. In the 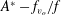 $A^{\ast }-f_{v_{o}}/f$ plane, the response data as well as other quantities related to free vibrations, for different
$A^{\ast }-f_{v_{o}}/f$ plane, the response data as well as other quantities related to free vibrations, for different 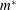 $m^{\ast }$, collapse on a curve. Unlike at high
$m^{\ast }$, collapse on a curve. Unlike at high 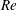 $Re$, the collapsed curves show a dependence on
$Re$, the collapsed curves show a dependence on 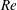 $Re$ in the laminar regime. The transition between the lock-in and desynchronized state, as seen from the collapsed curves, is qualitatively different for
$Re$ in the laminar regime. The transition between the lock-in and desynchronized state, as seen from the collapsed curves, is qualitatively different for 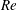 $Re$ on either side of
$Re$ on either side of 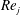 $Re_{j}$. The collapsed curves, at a certain
$Re_{j}$. The collapsed curves, at a certain 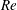 $Re$, are utilized to estimate
$Re$, are utilized to estimate 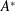 $A^{\ast }$ for the limiting case of
$A^{\ast }$ for the limiting case of 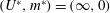 $(U^{\ast },m^{\ast })=(\infty ,0)$. Interestingly, unlike at large
$(U^{\ast },m^{\ast })=(\infty ,0)$. Interestingly, unlike at large 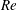 $Re$, this limit value is found to be lower than the peak amplitude of cylinder vibration at a given
$Re$, this limit value is found to be lower than the peak amplitude of cylinder vibration at a given 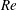 $Re$. Hysteresis in the cylinder response, near the higher-
$Re$. Hysteresis in the cylinder response, near the higher-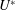 $U^{\ast }$ end of the lock-in regime, is explored. It is observed that the range of
$U^{\ast }$ end of the lock-in regime, is explored. It is observed that the range of 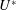 $U^{\ast }$ with hysteretic response increases with decrease in
$U^{\ast }$ with hysteretic response increases with decrease in 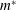 $m^{\ast }$. Interestingly, for a certain range of
$m^{\ast }$. Interestingly, for a certain range of 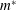 $m^{\ast }$, the response is hysteretic from a finite
$m^{\ast }$, the response is hysteretic from a finite 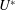 $U^{\ast }$ up to
$U^{\ast }$ up to 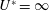 $U^{\ast }=\infty$. We refer to this phenomenon as hysteresis forever. It occurs because of the existence of multiple response states of the system at
$U^{\ast }=\infty$. We refer to this phenomenon as hysteresis forever. It occurs because of the existence of multiple response states of the system at 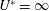 $U^{\ast }=\infty$, for a certain range of
$U^{\ast }=\infty$, for a certain range of 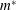 $m^{\ast }$. The study brings out the significant differences in the response of the fluid–structure system associated with the critical mass phenomenon between the low- and high-
$m^{\ast }$. The study brings out the significant differences in the response of the fluid–structure system associated with the critical mass phenomenon between the low- and high-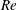 $Re$ regime.
$Re$ regime.
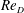 $Re_{D}$ from
$Re_{D}$ from 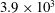 $3.9\times 10^{3}$ to
$3.9\times 10^{3}$ to 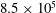 $8.5\times 10^{5}$: a skin-friction perspective
$8.5\times 10^{5}$: a skin-friction perspective
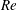 $Re$
$Re$