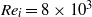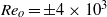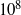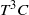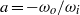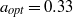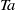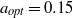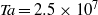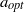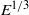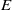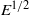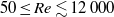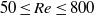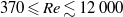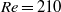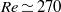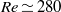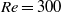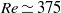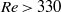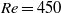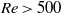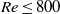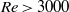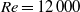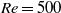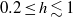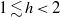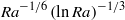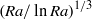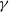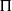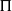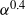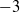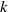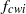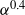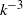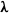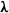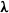A combined numerical and experimental study examining vortex-induced vibration (VIV) of a neutrally buoyant tethered sphere has been undertaken. The study covered the Reynolds-number range 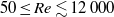 $50\leq \mathit{Re}\lesssim 12\hspace{0.167em} 000$, with the numerical (
$50\leq \mathit{Re}\lesssim 12\hspace{0.167em} 000$, with the numerical (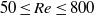 $50\leq \mathit{Re}\leq 800$) and experimental (
$50\leq \mathit{Re}\leq 800$) and experimental (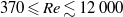 $370\leqslant \mathit{Re}\lesssim 12\hspace{0.167em} 000$) ranges overlapping. Neutral buoyancy was chosen to eliminate one parameter, i.e. the influence of gravity, on the VIV behaviour, although, of course, the effect of added mass remains. The tether length was also chosen to be sufficiently long so that, to a good approximation, the sphere was constrained to move within a plane. Seven broad but relatively distinct sphere oscillation and wake states could be distinguished. For regime I, the wake is steady and axisymmetric, and it undergoes transition to a steady two-tailed wake in regime II at
$370\leqslant \mathit{Re}\lesssim 12\hspace{0.167em} 000$) ranges overlapping. Neutral buoyancy was chosen to eliminate one parameter, i.e. the influence of gravity, on the VIV behaviour, although, of course, the effect of added mass remains. The tether length was also chosen to be sufficiently long so that, to a good approximation, the sphere was constrained to move within a plane. Seven broad but relatively distinct sphere oscillation and wake states could be distinguished. For regime I, the wake is steady and axisymmetric, and it undergoes transition to a steady two-tailed wake in regime II at 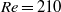 $\mathit{Re}= 210$. Those regimes are directly analogous to those of a fixed sphere. Once the sphere begins to vibrate at
$\mathit{Re}= 210$. Those regimes are directly analogous to those of a fixed sphere. Once the sphere begins to vibrate at 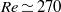 $\mathit{Re}\simeq 270$ in regime III, the wake behaviour is distinct from the fixed-sphere wake. Initially the vibration frequency of the sphere is half the shedding frequency in the wake, with the latter consistent with the fixed-sphere wake frequency. The sphere vibration is not purely periodic but modulated over several base periods. However, at slightly higher Reynolds numbers (
$\mathit{Re}\simeq 270$ in regime III, the wake behaviour is distinct from the fixed-sphere wake. Initially the vibration frequency of the sphere is half the shedding frequency in the wake, with the latter consistent with the fixed-sphere wake frequency. The sphere vibration is not purely periodic but modulated over several base periods. However, at slightly higher Reynolds numbers (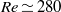 $\mathit{Re}\simeq 280$), planar symmetry is broken, and the vibration shifts to the planar normal (or azimuthal) direction, and becomes completely azimuthal at the start of regime IV at
$\mathit{Re}\simeq 280$), planar symmetry is broken, and the vibration shifts to the planar normal (or azimuthal) direction, and becomes completely azimuthal at the start of regime IV at 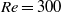 $\mathit{Re}= 300$. In comparison, for a fixed sphere, planar symmetry is broken at a much higher Reynolds number of
$\mathit{Re}= 300$. In comparison, for a fixed sphere, planar symmetry is broken at a much higher Reynolds number of 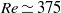 $\mathit{Re}\simeq 375$. Interestingly, planar symmetry returns to the wake for
$\mathit{Re}\simeq 375$. Interestingly, planar symmetry returns to the wake for 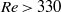 $\mathit{Re}\gt 330$, in regime V, for which the oscillations are again radial, and is maintained until
$\mathit{Re}\gt 330$, in regime V, for which the oscillations are again radial, and is maintained until 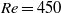 $\mathit{Re}= 450$ or higher. At the same time, the characteristic vortex loops in the wake become symmetrical, i.e. two-sided. For
$\mathit{Re}= 450$ or higher. At the same time, the characteristic vortex loops in the wake become symmetrical, i.e. two-sided. For 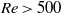 $\mathit{Re}\gt 500$, in regime VI, the trajectory of the sphere becomes irregular, possibly chaotic. That state is maintained over the remaining Reynolds-number range simulated numerically (
$\mathit{Re}\gt 500$, in regime VI, the trajectory of the sphere becomes irregular, possibly chaotic. That state is maintained over the remaining Reynolds-number range simulated numerically (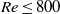 $\mathit{Re}\leq 800$). Experiments overlapping this Reynolds-number range confirm the amplitude radial oscillations in regime V and the chaotic wandering for regime VI. At still higher Reynolds numbers of
$\mathit{Re}\leq 800$). Experiments overlapping this Reynolds-number range confirm the amplitude radial oscillations in regime V and the chaotic wandering for regime VI. At still higher Reynolds numbers of 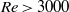 $\mathit{Re}\gt 3000$, in regime VII, the trajectories evolve to quasi-circular orbits about the neutral point, with the orbital radius increasing as the Reynolds number is increased. At
$\mathit{Re}\gt 3000$, in regime VII, the trajectories evolve to quasi-circular orbits about the neutral point, with the orbital radius increasing as the Reynolds number is increased. At 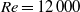 $\mathit{Re}= 12\hspace{0.167em} 000$, the orbital diameter reaches approximately one sphere diameter. Of interest, this transition sequence is distinct from that for a vertically tethered heavy sphere, which undergoes transition to quasi-circular orbits beyond
$\mathit{Re}= 12\hspace{0.167em} 000$, the orbital diameter reaches approximately one sphere diameter. Of interest, this transition sequence is distinct from that for a vertically tethered heavy sphere, which undergoes transition to quasi-circular orbits beyond 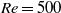 $\mathit{Re}= 500$.
$\mathit{Re}= 500$.