Hostname: page-component-848d4c4894-nmvwc Total loading time: 0 Render date: 2024-06-23T11:04:31.116Z Has data issue: false hasContentIssue false
  • English
  • Français

Recurrent solutions of the Alber equation initialized by Joint North Sea Wave Project spectra

Published online by Cambridge University Press:  19 February 2013

A. Ribal ,
A. V. Babanin ,
I. Young ,
A. Toffoli  and
M. Stiassnie
A. Ribal
Affiliation:
Centre for Ocean Engineering, Science and Technology, Swinburne University of Technology, Melbourne, VIC 3122, Australia
A. V. Babanin*
Affiliation:
Centre for Ocean Engineering, Science and Technology, Swinburne University of Technology, Melbourne, VIC 3122, Australia
I. Young
Affiliation:
The Australian National University, Canberra, ACT 0200, Australia
A. Toffoli
Affiliation:
Centre for Ocean Engineering, Science and Technology, Swinburne University of Technology, Melbourne, VIC 3122, Australia
M. Stiassnie
Affiliation:
Faculty of Civil and Environmental Engineering, Technion-Israel Institute of Technology, Haifa 32000, Israel
*
†Email address for correspondence: ABabanin@swin.edu.au
Get access Rights & Permissions [Opens in a new window]

Abstract

Linear instability of two-dimensional wave fields and its concurrent evolution in time is here investigated by means of the Alber equation for narrow-banded random surface waves in deep water subject to inhomogeneous disturbances. The probability of freak waves in the context of these simulations is also discussed. The instability is first studied for the symmetric Lorentz spectrum, and continued for the realistic asymmetric Joint North Sea Wave Project (JONSWAP) spectrum of ocean waves with variable directional spreading and steepness. 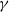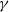It is found that instability depends on the directional spreading and parameters $\alpha $ and $\gamma $ of the JONSWAP spectrum, where $\alpha $ and $\gamma $ are the energy scale and the peak enhancement factor, respectively. Both influence the mean steepness of waves with such a spectrum, although in different ways. Specifically, if the instability stops as a result of the directional spreading, increase of the steepness by increasing $\alpha $ or 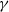$\gamma $ can reactivate it. A criterion for the instability is suggested as a dimensionless ‘width parameter’, 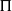$\Pi $. For the unstable conditions, long-time evolution is simulated by integrating the Alber equation numerically. Recurrent evolution is obtained, which is a stochastic counterpart of the Fermi–Pasta–Ulam recurrence obtained for the cubic Schrödinger equation. This recurrence enables us to study the probability of freak waves, and the results are compared to the values given by the Rayleigh distribution. Moreover, it is found that stability–instability transition, the most unstable mode, recurrence duration and freak wave probability depend solely on the dimensionless ‘width parameter’, 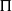$\Pi $.

JFM classification

Waves/Free-surface Flows: Surface gravity waves Waves/Free-surface Flows: Waves/Free-surface Flows
Type
Papers
Information
Journal of Fluid Mechanics , Volume 719 , 25 March 2013 , pp. 314 - 344
Copyright
©2013 Cambridge University Press

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

‡

Currently on leave from the Department of Mathematics, Hasanuddin University, Makassar, Indonesia.

References

Alber, I. E. 1978 The effects of randomness on the stability of two-dimensional surface wavetrains. Proc. R. Soc. Lond. A 363, 525–546.Google Scholar
Babanin, A. 2011 Breaking and Dissipation of Ocean Surface Waves, p. 485. Cambridge University Press.CrossRefGoogle Scholar
Babanin, A. V., Chalikov, D., Young, I. R. & Savelyev, I. 2010 Numerical and laboratory investigation of breaking of steep two-dimensional waves in deep water. J. Fluid Mech. 644, 433–463.CrossRefGoogle Scholar
Babanin, A. V. & Soloviev, Y. P. 1987 Parameterization of the width of angular-distribution of the wind wave energy at limited fetches. Izv. Akad. Nauk SSSR Fiz. Atmos. Okeana 23, 868–876.Google Scholar
Babanin, A. V. & Soloviev, Y. P. 1998a Field investigation of transformation of the wind wave frequency spectrum with fetch and the stage of development. J. Phys. Oceanogr. 28, 563–576.2.0.CO;2>CrossRefGoogle Scholar
Babanin, A. V. & Soloviev, Y. P. 1998b Variability of directional spectra of wind-generated waves, studied by means of wave staff arrays. Mar. Freshwat. Res. 49, 89–101.Google Scholar
Babanin, A. V., Waseda, T., Kinoshita, T. & Toffoli, A. 2011a Wave breaking in directional fields. J. Phys. Oceanogr. 41, 145–156.CrossRefGoogle Scholar
Babanin, A. V., Waseda, T., Shugan, I. & Hwung, H.-H. 2011b Modulational instability in directional wave fields and extreme wave events. In Proceedings of the ASME 2011 30th International Conference on Ocean, Offshore and Arctic Engineering, OMAE2011, 19–24 July 2011 Rotterdam, The Netherlands, Paper no. OMAE2011-49540, pp. 409–415. American Society of Mechanical Engineers.Google Scholar
Buckingham, E. 1914 On physically similar systems; illustrations of the use of dimensional equations. Phys. Rev. 4, 345–376.CrossRefGoogle Scholar
Crawford, D. R., Saffman, P. G. & Yuen, H. C. 1980 Evolution of a random inhomogeneous field of nonlinear deep-water gravity waves. Wave Motion 2, 1–16.Google Scholar
Dysthe, K. B., Trulsen, K., Krogstad, H. E. & Socquet-Juglard, H. 2003 Evolution of a narrow-band spectrum of random surface gravity waves. J. Fluid Mech. 478, 1–10.Google Scholar
Eliasson, B. & Shukla, P. K. 2010 Numerical investigation of the instability and nonlinear evolution of narrow-band directional ocean waves. Phys. Rev. Lett. 105, 014501.CrossRefGoogle ScholarPubMed
Galchenko, A., Babanin, A. V., Chalikov, D., Young, I. R. & Haus, B. K. 2012 Influence of wind forcing on modulation and breaking of one-dimensional deep-water wave groups. J. Phys. Oceanogr. 42, 928–939.Google Scholar
Gramstad, O. & Trulsen, K. 2007 Influence of crest and group length on the occurrence of freak waves. J. Fluid Mech. 582, 463–472.Google Scholar
Hasselmann, K. 1962 On the non-linear energy transfer in a gravity-wave spectrum, Part 1. General theory. J. Fluid Mech. 12, 481–500.CrossRefGoogle Scholar
Holthuijsen, L. H. 2007 Waves in Oceanic and Coastal Waters. Cambridge University Press.CrossRefGoogle Scholar
Janssen, P. A. E. M. 1981 Modulational instability and the Fermi–Pasta–Ulam recurrence. Phys. Fluids 24, 23–26.CrossRefGoogle Scholar
Janssen, P. A. E. M. 2003 Nonlinear four-wave interactions and freak waves. J. Phys. Oceanogr. 33, 863–884.2.0.CO;2>CrossRefGoogle Scholar
Kharif, C. & Pelinovsky, E. 2003 Physical mechanisms of the rogue wave phenomenon. Eur. J. Mech. B/Fluids 22, 603–634.CrossRefGoogle Scholar
Komen, G. J., Cavaleri, L., Donelan, M., Hasselmann, K., Hasselmann, S. & Janssen, P. A. E. M. 1994 Dynamics and Modelling of Ocean Waves. Cambridge University Press.CrossRefGoogle Scholar
Landsberg, H. E. 1955 Advances in Geophysics, vol. 2. Elsevier.Google Scholar
Longuet-Higgins, M. S. 1952 On the statistical distribution of the heights of sea waves. J. Mar. Res. 11, 245–266.Google Scholar
Longuet-Higgins, M. S. 1976 On the nonlinear transfer of energy in the peak of a gravity-wave spectrum: a simplified model. Proc. R. Soc. Lond. A 347, 311–328.Google Scholar
Mori, N., Onorato, M. & Janssen, P. A. E. M. 2011 On the estimation of the kurtosis in directional sea states for freak wave forecasting. J. Phys. Oceanogr. 41, 1484–1497.CrossRefGoogle Scholar
Mori, N., Onorato, M., Janssen, P. A. E. M., Osborne, A. R. & Serio, M. 2007 On the extreme statistics of long-crested deep water waves: theory and experiments. J. Geophys. Res. 112, C09011 doi:10.1029/2006JC004024.Google Scholar
Onorato, M., Cavaleri, L., Fouques, S., Gramstad, O., Janssen, P. A. E. M., Monbaliu, J., Osborne, A. R., Pakozdi, C., Serio, M., Stansberg, C. T., Toffoli, A. & Trulsen, K. 2009a Statistical properties of mechanically generated surface gravity waves: a laboratory experiment in a three-dimensional wave basin. J. Fluid Mech. 627, 235–257.Google Scholar
Onorato, M., Osborne, A., Fedele, R. & Serio, M. 2003 Landau damping and coherent structures in narrow-banded 1 + 1 deep water gravity waves. Phys. Rev. E 67, 046305.CrossRefGoogle ScholarPubMed
Onorato, M., Osborne, A. R. & Serio, M. 2002 Extreme wave events in directional, random oceanic sea states. Phys. Fluids 14, 25–28.CrossRefGoogle Scholar
Onorato, M., Osborne, A. R., Serio, M. & Bertone, S. 2001 Freak waves in random oceanic sea states. Phys. Rev. Lett. 86, 5831–5834.CrossRefGoogle ScholarPubMed
Onorato, M., Osborne, A. R., Serio, M., Cavaleri, L., Brandini, C. & Stansberg, C. T. 2004 Observation of strongly non-Gaussian statistics for random sea surface gravity waves in wave flume experiments. Phys. Rev. E 70, 067302.CrossRefGoogle ScholarPubMed
Onorato, M. & Proment, D. 2012 Approximate rogue wave solutions of the forced and damped nonlinear Schrödinger equation for water waves. Phys. Lett. A 376, 3057–3059.Google Scholar
Onorato, M., Waseda, T., Toffoli, A., Cavaleri, L., Gramstad, O., Janssen, P. A. E. M., Kinoshita, T., Monbaliu, J., Mori, N., Osborne, A. R., Serio, M., Stansberg, C. T., Tamura, H. & Trulsen, K. 2009b Statistical properties of directional ocean waves: the role of the modulational instability in the formation of extreme events. Phys. Rev. Lett. 102, 114502.Google Scholar
Pierson, W. J. 1955 Wind generated gravity waves. Adv. Geophys. 2, 93–178.CrossRefGoogle Scholar
Regev, A., Agnon, Y., Stiassnie, M. & Gramstad, O. 2008 Sea-swell interaction as a mechanism for the generation of freak waves. Phys. Fluids 20, 112102.CrossRefGoogle Scholar
Socquet-Juglard, H., Dysthe, K., Trulsen, K., Krogstad, H. E. & Liu, J. 2005 Probability distributions of surface gravity waves during spectral changes. J. Fluid Mech. 542, 195–216.Google Scholar
Stiassnie, M. & Kroszynski, U. I. 1982 Long-time evolution of an unstable water-wave train. J. Fluid Mech. 116, 207–225.Google Scholar
Stiassnie, M., Regev, A. & Agnon, Y. 2008 Recurrent solutions of Alber’s equation for random water-wave fields. J. Fluid Mech. 598, 245–266.CrossRefGoogle Scholar
Toffoli, A., Babanin, A., Onorato, M. & Waseda, T. 2010a Maximum steepness of oceanic waves: field and laboratory. Geophys. Res. Lett. 37, L05603 doi:10.1029/2009GL041771.Google Scholar
Toffoli, A., Gramstad, O., Trulsen, K., Monbaliu, J., Bitner-Gregersen, E. & Onorato, M. 2010b Evolution of weakly nonlinear random directional waves: laboratory experiments and numerical simulations. J. Fluid Mech. 664, 313–336.Google Scholar
Trulsen, K. & Dysthe, K. 1992 Action of windstress and breaking on the evolution of a wavetrain. In Breaking Waves (ed. Banner, M. & Grimshaw, R.), pp. 243–249. Springer.CrossRefGoogle Scholar
Waseda, T., Kinoshita, T. & Tamura, H. 2009 Evolution of a random directional wave and freak wave occurrence. J. Phys. Oceanogr. 39, 621–639.Google Scholar
Young, I. R. 1999 Wind Generated Ocean Waves. Elsevier Science.Google Scholar
Yuen, H. C. & Ferguson, W. E. Jr. 1978a Fermi–Pasta–Ulam recurrence in the two-space dimensional nonlinear Schrödinger equation. Phys. Fluids 21, 2116–2118.CrossRefGoogle Scholar
Yuen, H. C. & Ferguson, W. E. Jr. 1978b Relationship between Benjamin–Feir instability and recurrence in the nonlinear Schrödinger equation. Phys. Fluids 21, 1275–1278.CrossRefGoogle Scholar
Zakharov, V. E. 1968 Stability of periodic waves of finite amplitude on the surface of a deep fluid. J. Appl. Mech. Tech. Phys. 9, 190–194.Google Scholar