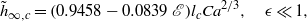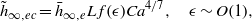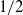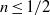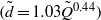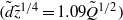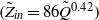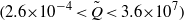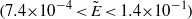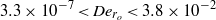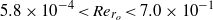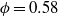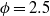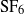Papers
The elastocapillary Landau–Levich problem
-
- Published online by Cambridge University Press:
- 16 October 2013, pp. 1-28
-
- Article
- Export citation
Thin power-law film flow down an inclined plane: consistent shallow-water models and stability under large-scale perturbations
-
- Published online by Cambridge University Press:
- 16 October 2013, pp. 29-60
-
- Article
- Export citation
Shock reflection in the presence of an upstream expansion wave and a downstream shock wave
-
- Published online by Cambridge University Press:
- 22 October 2013, pp. 61-90
-
- Article
- Export citation
Body-rock or lift-off in flow
-
- Published online by Cambridge University Press:
- 22 October 2013, pp. 91-119
-
- Article
- Export citation
Liquid–solid impacts with compressible gas cushioning
-
- Published online by Cambridge University Press:
- 22 October 2013, pp. 120-149
-
- Article
- Export citation
New correlation formulae for the straight section of the electrospun jet from a polymer drop
-
- Published online by Cambridge University Press:
- 23 October 2013, pp. 150-175
-
- Article
- Export citation
Cyclic flame propagation in premixed combustion
-
- Published online by Cambridge University Press:
- 23 October 2013, pp. 176-202
-
- Article
- Export citation
On the highest non-breaking wave in a group: fully nonlinear water wave breathers versus weakly nonlinear theory
-
- Published online by Cambridge University Press:
- 23 October 2013, pp. 203-248
-
- Article
- Export citation
Weakly nonlinear instability of planar viscous sheets
-
- Published online by Cambridge University Press:
- 23 October 2013, pp. 249-287
-
- Article
- Export citation
Evolution of the density self-correlation in developing Richtmyer–Meshkov turbulence
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 288-306
-
- Article
-
- You have access
- Open access
- Export citation
Flow past a rotationally oscillating cylinder
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 307-346
-
- Article
- Export citation
Free-stream turbulence and the development of cross-flow disturbances
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 347-380
-
- Article
- Export citation
Turbulent structure of high-amplitude pressure peaks within the turbulent boundary layer
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 381-426
-
- Article
- Export citation
Electrified coating flows on vertical fibres: enhancement or suppression of interfacial dynamics
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 427-456
-
- Article
- Export citation
On the measurement of turbulent magnetic diffusivities: the three-dimensional case
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 457-472
-
- Article
- Export citation
Wall effects on self-diffusiophoretic Janus particles: a theoretical study
-
- Published online by Cambridge University Press:
- 24 October 2013, pp. 473-498
-
- Article
- Export citation
Available potential energy density for a multicomponent Boussinesq fluid with arbitrary nonlinear equation of state
-
- Published online by Cambridge University Press:
- 25 October 2013, pp. 499-518
-
- Article
- Export citation
Effect of surfactant on two-layer channel flow
-
- Published online by Cambridge University Press:
- 25 October 2013, pp. 519-552
-
- Article
- Export citation
Laminar and transitional liquid metal duct flow near a magnetic point dipole
-
- Published online by Cambridge University Press:
- 28 October 2013, pp. 553-586
-
- Article
- Export citation
Three-dimensional flow within shallow, narrow cavities
-
- Published online by Cambridge University Press:
- 28 October 2013, pp. 587-612
-
- Article
- Export citation