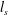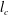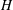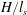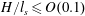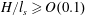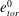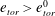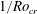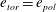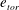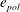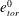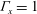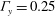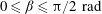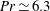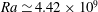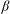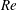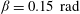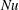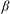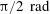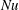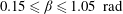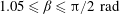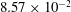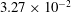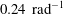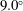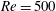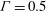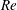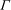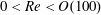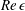Focus on Fluids
The bearable gooeyness of swimming
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
Papers
Centrifugal, barotropic and baroclinic instabilities of isolated ageostrophic anticyclones in the two-layer rotating shallow water model and their nonlinear saturation
-
- Published online by Cambridge University Press:
- 27 November 2014, pp. 5-34
-
- Article
- Export citation
Erosion–deposition waves in shallow granular free-surface flows
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 35-67
-
- Article
- Export citation
Films in narrow tubes
-
- Published online by Cambridge University Press:
- 27 November 2014, pp. 68-109
-
- Article
- Export citation
The morphodynamics of a swash event on an erodible beach
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 110-140
-
- Article
- Export citation
Helical vortex filament motion under the non-local Biot–Savart model
-
- Published online by Cambridge University Press:
- 03 December 2014, pp. 141-155
-
- Article
- Export citation
Sediment-laden fresh water above salt water: nonlinear simulations
-
- Published online by Cambridge University Press:
- 27 November 2014, pp. 156-195
-
- Article
- Export citation
Ellipsoidal vortices in rotating stratified fluids: beyond the quasi-geostrophic approximation
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 196-231
-
- Article
- Export citation
Toroidal and poloidal energy in rotating Rayleigh–Bénard convection
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 232-255
-
- Article
- Export citation
Submesoscale baroclinic instability in the balance equations
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 256-272
-
- Article
- Export citation
The effect of cell tilting on turbulent thermal convection in a rectangular cell
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 273-287
-
- Article
- Export citation
Deformation of a spherical capsule under oscillating shear flow
-
- Published online by Cambridge University Press:
- 02 December 2014, pp. 288-301
-
- Article
- Export citation
Organised large structure in the post-transition mixing layer. Part 2. Large-eddy simulation
-
- Published online by Cambridge University Press:
- 03 December 2014, pp. 302-343
-
- Article
- Export citation
Experimental investigation of stationary and rotational structures in non-circular hydraulic jumps
-
- Published online by Cambridge University Press:
- 03 December 2014, pp. 344-360
-
- Article
- Export citation
Sensitivity and open-loop control of stochastic response in a noise amplifier flow: the backward-facing step
-
- Published online by Cambridge University Press:
- 03 December 2014, pp. 361-392
-
- Article
- Export citation
Experimental and theoretical study of dewetting corner flow
-
- Published online by Cambridge University Press:
- 03 December 2014, pp. 393-416
-
- Article
- Export citation
Gravity current propagation up a valley
-
- Published online by Cambridge University Press:
- 04 December 2014, pp. 417-434
-
- Article
- Export citation
Buoyancy-induced turbulence in a tilted pipe
-
- Published online by Cambridge University Press:
- 08 December 2014, pp. 435-477
-
- Article
- Export citation
Rapids
On the thermodynamic boundary conditions of a solidifying mushy layer with outflow
-
- Published online by Cambridge University Press:
- 27 November 2014, R1
-
- Article
- Export citation
Instabilities in a fluid overlying an inclined anisotropic and inhomogeneous porous layer
-
- Published online by Cambridge University Press:
- 27 November 2014, R2
-
- Article
- Export citation