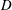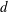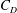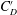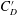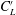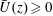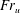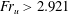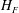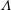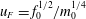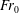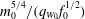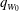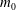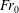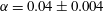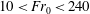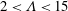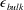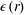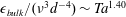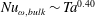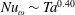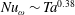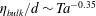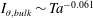Focus on Fluids
‘Shear thickening’ in non-shear flows: the effect of microstructure
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 1-4
-
- Article
-
- You have access
- HTML
- Export citation
JFM Papers
Two tandem cylinders of different diameters in cross-flow: effect of an upstream cylinder on wake dynamics
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 5-42
-
- Article
- Export citation
Transition to turbulence in the rotating-disk boundary-layer flow with stationary vortices
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 43-71
-
- Article
- Export citation
Models of energy loss from internal waves breaking in the ocean
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 72-116
-
- Article
- Export citation
Aerodynamic noise from rigid trailing edges with finite porous extensions
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 117-144
-
- Article
- Export citation
Vortex force map method for viscous flows of general airfoils
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 145-166
-
- Article
- Export citation
Roughness-induced transition by quasi-resonance of a varicose global mode
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 167-191
-
- Article
- Export citation
Internal wave generation by tidal flow over a two-dimensional ridge: energy flux asymmetries induced by a steady surface trapped current
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 192-221
-
- Article
- Export citation
Implication of Taylor’s hypothesis on measuring flow modulation
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 222-237
-
- Article
- Export citation
The evolution of second mode internal solitary waves over variable topography
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 238-259
-
- Article
- Export citation
A note on analytic solutions for entraining stratified gravity currents
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 260-276
-
- Article
- Export citation
Turbulent bubble fountains
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 277-303
-
- Article
- Export citation
Bistability in the synchronization of actuated microfilaments
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 304-323
-
- Article
- Export citation
Diffusion and mixing effects in hot jet initiation and propagation of hydrogen detonations
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 324-351
-
- Article
- Export citation
Sound signals of tsunamis from a slender fault
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 352-373
-
- Article
- Export citation
Labyrinthine and secondary wave instabilities of a miscible magnetic fluid drop in a Hele-Shaw cell
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 374-396
-
- Article
- Export citation
Turbulence strength in ultimate Taylor–Couette turbulence
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 397-412
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Equilibrium structure and diffusion in concentrated hydrodynamically interacting suspensions confined by a spherical cavity
-
- Published online by Cambridge University Press:
- 11 December 2017, pp. 413-450
-
- Article
- Export citation
Higher-order moment theories for dilute granular gases of smooth hard spheres
-
- Published online by Cambridge University Press:
- 12 December 2017, pp. 451-501
-
- Article
- Export citation
On the viscous flows of leak-out and spherical cap natation
-
- Published online by Cambridge University Press:
- 12 December 2017, pp. 502-531
-
- Article
- Export citation