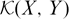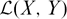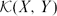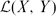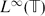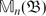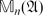Research Article
THE DEPENDENCE OF THE FIRST EIGENVALUE OF THE INFINITY LAPLACIAN WITH RESPECT TO THE DOMAIN
-
- Published online by Cambridge University Press:
- 02 September 2013, pp. 241-249
-
- Article
-
- You have access
- Export citation
BIEMBEDDINGS OF STEINER TRIPLE SYSTEMS IN ORIENTABLE PSEUDOSURFACES WITH ONE PINCH POINT
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 251-260
-
- Article
-
- You have access
- Export citation
GEOGRAPHY AND BOTANY OF IRREDUCIBLE NON-SPIN SYMPLECTIC 4-MANIFOLDS WITH ABELIAN FUNDAMENTAL GROUP
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 261-281
-
- Article
-
- You have access
- Export citation
AN OBATA-TYPE THEOREM ON A THREE-DIMENSIONAL CR MANIFOLD
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 283-294
-
- Article
-
- You have access
- Export citation
POSITIVE ENERGY REPRESENTATIONS AND CONTINUITY OF PROJECTIVE REPRESENTATIONS FOR GENERAL TOPOLOGICAL GROUPS
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 295-316
-
- Article
-
- You have access
- Export citation
A VARIATIONAL APPROACH FOR A BI-NON-LOCAL ELLIPTIC PROBLEM INVOLVING THE p(x)-LAPLACIAN AND NON-LINEARITY WITH NON-STANDARD GROWTH
-
- Published online by Cambridge University Press:
- 20 August 2013, pp. 317-333
-
- Article
-
- You have access
- Export citation
THE EQUIVALENCE OF RUBIN'S CONJECTURE AND THE ETNC/LRNC FOR CERTAIN BIQUADRATIC EXTENSIONS
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 335-353
-
- Article
-
- You have access
- Export citation
ORE EXTENSIONS AND POISSON ALGEBRAS
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 355-368
-
- Article
-
- You have access
- Export citation
A DESCENT SPECTRAL SEQUENCE FOR ARBITRARY K(n)-LOCAL SPECTRA WITH EXPLICIT E2-TERM
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 369-380
-
- Article
-
- You have access
- Export citation
A GENERALIZATION OF THE SWARTZ EQUALITY
-
- Published online by Cambridge University Press:
- 30 August 2013, pp. 381-386
-
- Article
-
- You have access
- Export citation
GROUPS OF INFINITE RANK IN WHICH NORMALITY IS A TRANSITIVE RELATION
-
- Published online by Cambridge University Press:
- 30 August 2013, pp. 387-393
-
- Article
-
- You have access
- Export citation
ALMOST ISOMETRIC IDEALS IN BANACH SPACES
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 395-407
-
- Article
-
- You have access
- Export citation
THE POSITION OF
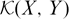 $\mathcal{K}(X,Y)$ IN
$\mathcal{K}(X,Y)$ IN 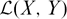 $\mathcal{L}(X,Y)$
$\mathcal{L}(X,Y)$
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 409-417
-
- Article
-
- You have access
- Export citation
BANACH ALGEBRAS OF VECTOR-VALUED FUNCTIONS
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 419-426
-
- Article
-
- You have access
- Export citation
AN OPERATOR SUMMABILITY OF SEQUENCES IN BANACH SPACES
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 427-437
-
- Article
-
- You have access
- Export citation
GROUP ACTIONS AND COVERINGS OF BRAUER GRAPH ALGEBRAS
-
- Published online by Cambridge University Press:
- 30 August 2013, pp. 439-464
-
- Article
-
- You have access
- Export citation
IMAGES OF WORD MAPS IN FINITE SIMPLE GROUPS
-
- Published online by Cambridge University Press:
- 30 August 2013, pp. 465-469
-
- Article
-
- You have access
- Export citation
SUBMODULES OF COMMUTATIVE C*-ALGEBRAS
-
- Published online by Cambridge University Press:
- 13 August 2013, pp. 471-479
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
GMJ volume 56 issue 2 Cover and Front matter
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. f1-f2
-
- Article
-
- You have access
- Export citation
Back Cover (IBC, OBC) and matter
GMJ volume 56 issue 2 Cover and Back matter
-
- Published online by Cambridge University Press:
- 01 April 2014, pp. b1-b2
-
- Article
-
- You have access
- Export citation