Hostname: page-component-8448b6f56d-mp689 Total loading time: 0 Render date: 2024-04-16T05:40:14.468Z Has data issue: false hasContentIssue false
  • English
  • Français

POSITIVE ENERGY REPRESENTATIONS AND CONTINUITY OF PROJECTIVE REPRESENTATIONS FOR GENERAL TOPOLOGICAL GROUPS

Published online by Cambridge University Press:  13 August 2013

KARL-HERMANN NEEB
KARL-HERMANN NEEB*
Affiliation:
Department Mathematik, FAU Erlangen-Nürnberg, Cauerstrasse 11, 91058 Erlangen, Germany e-mail: neeb@math.fau.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Let G and T be topological groups, α : T → Aut(G) a homomorphism defining a continuous action of T on G and G♯ := G ⋊αT the corresponding semidirect product group. In this paper, we address several issues concerning irreducible continuous unitary representations (π♯, 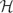${\mathcal{H}}$) of G♯ whose restriction to G remains irreducible. First, we prove that, for T = 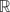${\mathbb R}$, this is the case for any irreducible positive energy representation of G♯, i.e. for which the one-parameter group Ut := π♯(1,t) has non-negative spectrum. The passage from irreducible unitary representations of G to representations of G♯ requires that certain projective unitary representations are continuous. To facilitate this verification, we derive various effective criteria for the continuity of projective unitary representations. Based on results of Borchers for W*-dynamical systems, we also derive a characterization of the continuous positive definite functions on G that extend to G♯.

Keywords

22E4522E6622D1043A65
Type
Research Article
Information
Glasgow Mathematical Journal , Volume 56 , Issue 2 , May 2014 , pp. 295 - 316
Copyright
Copyright © Glasgow Mathematical Journal Trust 2013 

References

REFERENCES

1.Beltita, D. and Neeb, K.-H., Schur–Weyl theory for C*-algebras, Math. Nachr. 285 (10) (2012), 1170–1198.Google Scholar
2.Borchers, H.-J., On the implementability of automorphism groups, Commun. Math. Phys. 14 (1969), 305–314.Google Scholar
3.Borchers, H.-J., C*-algebras and automorphism groups, Commun. Math. Phys. 88 (1983), 95–103.CrossRefGoogle Scholar
4.Borchers, H.-J., Symmetry groups of C*-algebras and associated von Neumann algebras, in Dynamical systems of complex and irregular systems (Blanchard, P., et al., Editors), (World Scientific, River Edge, NJ, 1993), 12–21.Google Scholar
5.Borchers, H.-J., Translation group and particle representations in quantum field theory, Lecture Notes in Physics (Springer-Verlag, Berlin, Heidelberg, 1996).Google Scholar
6.Bratteli, O. and Robinson, D. W., Operator algebras and quantum statistical mechanics I, 2nd ed., Texts and Monographs in Physics (Springer, New York, Heidelberg, Berlin, 2002).Google Scholar
7.Cattaneo, U., Continuous unitary projective representations of Polish groups: The BMS-group, in Group theoretical methods in physics (Janner, A., et al., Editors), (Fourth Internat. Colloq., Nijmegen, 1975), Lecture Notes in Physics, vol. 50 (Springer, Berlin, 1976), 450–460.Google Scholar
8.Dixmier, J., Les C*-algèbres et leurs représentations (Gauthier-Villars, Paris, 1964).Google Scholar
9.Glöckner, H. and Neeb, K.-H., Minimally almost periodic abelian groups and commutative W*-algebras, in Nuclear groups and Lie groups (Peinador, E. M., et al., Editors) Research and Exposition in Mathematical, vol. 24 (Heldermann Verlag, Berlin, 2000), 163–186.Google Scholar
10.Magyar, M., Continuous linear representations, North-Holland Math. Studies, vol. 168 (North-Holland Publishing Co., Amsterdam, 1992).Google Scholar
11.Neeb, K.-H., Holomorphy and convexity in Lie theory, Expositions in Mathematics, vol. 28 (de Gruyter Verlag, Berlin, 2000).Google Scholar
12.Neeb, K.-H., Towards a Lie theory of locally convex groups, Japan J. Math. 1 (2) (2006), 291–468.Google Scholar
13.Neeb, K.-H., Holomorphic realization of unitary representations of Banach–Lie groups, in Lie Groups: Structure, Actions, and Representations, Progress in Mathematics (Huckleberry, A., et al., Editors), (arXiv:1011.1210v1) (2010).Google Scholar
14.Neeb, K.-H., Semibounded unitary representations of double extensions of Hilbert–Loop groups (arXiv:1205.5201) (2012).Google Scholar
15.Neeb, K.-H. and Wagemann, F., Lie group structures on groups of smooth and holomorphic maps, Geom. Dedicata 134 (2008), 17–60.Google Scholar
16.Neeb, K.-H. and Zellner, Ch., Oscillator algebras with semi-equicontinuous coadjoint orbits, Differ. Geom. Appl. 31 (2) (2013), 268–283.CrossRefGoogle Scholar
17.Pressley, A. and Segal, G., Loop groups (Oxford University Press, Oxford, 1986).Google Scholar
18.Rieffel, M. A., Unitary representations of group extensions: An algebraic approach to the theory of Mackey and Blattner, in Studies in analysis (Rota, G.-C., Editor), Adv. Math. Suppl. Stud., vol. 4 (Academic Press, New York, London, 1979), 43–82.Google Scholar
19.Sakai, S., C*-Algebras and W*-algebras (Springer-Verlag, New York, 1971).Google Scholar
20.Zellner, Ch., Semibounded representations of oscillator groups, Dissertation (FAU Erlangen–Nuremberg, 2013).Google Scholar