Article contents
THE POSITION OF 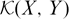 $\mathcal{K}(X,Y)$ IN
$\mathcal{K}(X,Y)$ IN 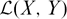 $\mathcal{L}(X,Y)$
$\mathcal{L}(X,Y)$
Published online by Cambridge University Press: 13 August 2013
Abstract
In this paper we investigate the nature of family of pairs of separable Banach spaces (X, Y) such that 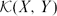 $\mathcal{K}(X,Y)$ is complemented in
$\mathcal{K}(X,Y)$ is complemented in 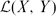 $\mathcal{L}(X,Y)$. It is proved that the family of pairs (X,Y) of separable Banach spaces such that
$\mathcal{L}(X,Y)$. It is proved that the family of pairs (X,Y) of separable Banach spaces such that 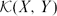 $\mathcal{K}(X,Y)$ is complemented in
$\mathcal{K}(X,Y)$ is complemented in 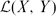 $\mathcal{L}(X,Y)$ is not Borel, endowed with the Effros–Borel structure.
$\mathcal{L}(X,Y)$ is not Borel, endowed with the Effros–Borel structure.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2013
References
REFERENCES
- 2
- Cited by


