Article contents
GEOGRAPHY AND BOTANY OF IRREDUCIBLE NON-SPIN SYMPLECTIC 4-MANIFOLDS WITH ABELIAN FUNDAMENTAL GROUP
Published online by Cambridge University Press: 13 August 2013
Abstract
The geography and botany problems of irreducible non-spin symplectic 4-manifolds with a choice of fundamental group from 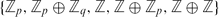 $\{{\mathbb{Z}}_p, {\mathbb{Z}}_p\oplus {\mathbb{Z}}_q, {\mathbb{Z}}, {\mathbb{Z}}\oplus {\mathbb{Z}}_p, {\mathbb{Z}}\oplus {\mathbb{Z}}\}$ are studied by building upon the recent progress obtained on the simply connected realm. Results on the botany of simply connected 4-manifolds not available in the literature are extended.
$\{{\mathbb{Z}}_p, {\mathbb{Z}}_p\oplus {\mathbb{Z}}_q, {\mathbb{Z}}, {\mathbb{Z}}\oplus {\mathbb{Z}}_p, {\mathbb{Z}}\oplus {\mathbb{Z}}\}$ are studied by building upon the recent progress obtained on the simply connected realm. Results on the botany of simply connected 4-manifolds not available in the literature are extended.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Glasgow Mathematical Journal Trust 2013
References
REFERENCES
- 2
- Cited by


