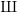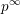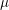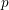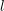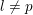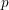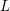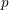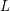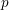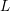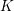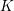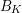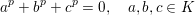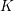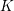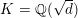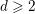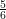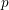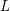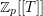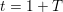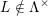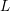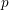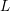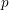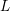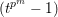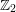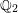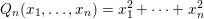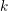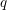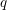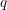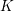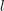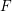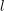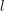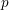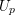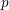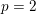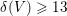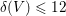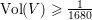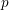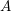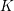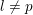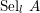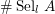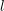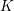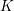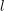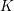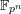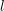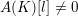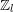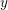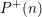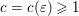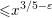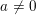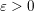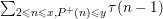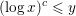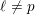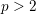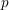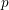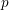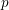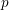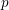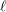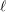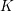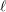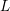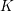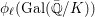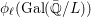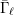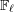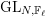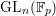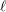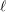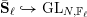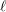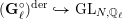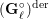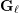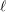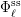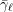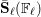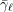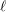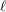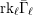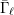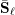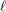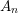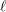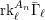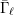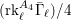Research Article
Growth of
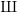 $\unicode[STIX]{x0428}$ in towers for isogenous curves
$\unicode[STIX]{x0428}$ in towers for isogenous curves
- Part of:
-
- Published online by Cambridge University Press:
- 30 June 2015, pp. 1981-2005
-
- Article
-
- You have access
- Export citation
The
 $p$-adic
$p$-adic 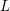 $L$-functions of evil Eisenstein series
$L$-functions of evil Eisenstein series
- Part of:
-
- Published online by Cambridge University Press:
- 13 January 2015, pp. 999-1040
-
- Article
-
- You have access
- Export citation
Beyond endoscopy via the trace formula: 1. Poisson summation and isolation of special representations
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1791-1820
-
- Article
-
- You have access
- Export citation
The asymptotic Fermat’s Last Theorem for five-sixths of real quadratic fields
- Part of:
-
- Published online by Cambridge University Press:
- 06 March 2015, pp. 1395-1415
-
- Article
-
- You have access
- Export citation
Formal Fourier Jacobi expansions and special cycles of codimension two
- Part of:
-
- Published online by Cambridge University Press:
- 06 August 2015, pp. 2187-2211
-
- Article
-
- You have access
- Export citation
Big Galois representations and
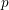 $p$-adic
$p$-adic 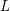 $L$-functions
$L$-functions
- Part of:
-
- Published online by Cambridge University Press:
- 13 November 2014, pp. 603-664
-
- Article
-
- You have access
- Export citation
Group schemes and local densities of quadratic lattices in residue characteristic 2
- Part of:
-
- Published online by Cambridge University Press:
- 05 December 2014, pp. 793-827
-
- Article
-
- You have access
- Export citation
Spectral theory for the
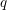 $q$-Boson particle system
$q$-Boson particle system
- Part of:
-
- Published online by Cambridge University Press:
- 17 September 2014, pp. 1-67
-
- Article
-
- You have access
- Export citation
Euler systems for modular forms over imaginary quadratic fields
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1585-1625
-
- Article
-
- You have access
- Export citation
Automorphy and irreducibility of some l-adic representations
- Part of:
-
- Published online by Cambridge University Press:
- 24 October 2014, pp. 207-229
-
- Article
-
- You have access
- Export citation
Level 1 Hecke algebras of modular forms modulo
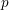 $p$
$p$
- Part of:
-
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
-
- Article
-
- You have access
- Export citation
Pairs of quadrics in 11 variables
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2015, pp. 1189-1214
-
- Article
-
- You have access
- Export citation
Explicit birational geometry of 3-folds and 4-folds of general type, III
- Part of:
-
- Published online by Cambridge University Press:
- 30 December 2014, pp. 1041-1082
-
- Article
-
- You have access
- Export citation
On the smooth transfer for Guo–Jacquet relative trace formulae
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 1821-1877
-
- Article
-
- You have access
- Export citation
Selmer groups and class groups
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 416-434
-
- Article
-
- You have access
- Export citation
Théorèmes de type Fouvry–Iwaniec pour les entiers friables
- Part of:
-
- Published online by Cambridge University Press:
- 03 March 2015, pp. 828-862
-
- Article
-
- You have access
- Export citation
Compatibility of arithmetic and algebraic local constants (the case
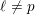 $\ell \neq p$)
$\ell \neq p$)
- Part of:
-
- Published online by Cambridge University Press:
- 08 April 2015, pp. 1626-1646
-
- Article
-
- You have access
- Export citation
Hecke characters associated to Drinfeld modular forms
- Part of:
-
- Published online by Cambridge University Press:
- 01 June 2015, pp. 2006-2058
-
- Article
-
- You have access
- Export citation
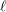 $\ell$-independence for compatible systems of (mod
$\ell$-independence for compatible systems of (mod 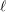 $\ell$) representations
$\ell$) representations
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2015, pp. 1215-1241
-
- Article
-
- You have access
- Export citation
Pseudoholomorphic tori in the Kodaira–Thurston manifold
- Part of:
-
- Published online by Cambridge University Press:
- 16 July 2015, pp. 2212-2250
-
- Article
-
- You have access
- Export citation