Article contents
Selmer groups and class groups
Published online by Cambridge University Press: 11 November 2014
Abstract
Let 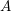 $A$ be an abelian variety over a global field
$A$ be an abelian variety over a global field 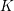 $K$ of characteristic
$K$ of characteristic 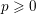 $p\geqslant 0$. If
$p\geqslant 0$. If 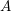 $A$ has nontrivial (respectively full)
$A$ has nontrivial (respectively full) 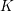 $K$-rational
$K$-rational 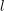 $l$-torsion for a prime
$l$-torsion for a prime 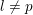 $l\neq p$, we exploit the fppf cohomological interpretation of the
$l\neq p$, we exploit the fppf cohomological interpretation of the 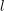 $l$-Selmer group
$l$-Selmer group 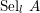 $\text{Sel}_{l}\,A$ to bound
$\text{Sel}_{l}\,A$ to bound 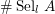 $\#\text{Sel}_{l}\,A$ from below (respectively above) in terms of the cardinality of the
$\#\text{Sel}_{l}\,A$ from below (respectively above) in terms of the cardinality of the 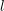 $l$-torsion subgroup of the ideal class group of
$l$-torsion subgroup of the ideal class group of 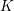 $K$. Applied over families of finite extensions of
$K$. Applied over families of finite extensions of 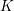 $K$, the bounds relate the growth of Selmer groups and class groups. For function fields, this technique proves the unboundedness of
$K$, the bounds relate the growth of Selmer groups and class groups. For function fields, this technique proves the unboundedness of 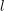 $l$-ranks of class groups of quadratic extensions of every
$l$-ranks of class groups of quadratic extensions of every 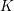 $K$ containing a fixed finite field
$K$ containing a fixed finite field 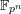 $\mathbb{F}_{p^{n}}$ (depending on
$\mathbb{F}_{p^{n}}$ (depending on 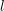 $l$). For number fields, it suggests a new approach to the Iwasawa
$l$). For number fields, it suggests a new approach to the Iwasawa 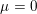 ${\it\mu}=0$ conjecture through inequalities, valid when
${\it\mu}=0$ conjecture through inequalities, valid when 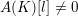 $A(K)[l]\neq 0$, between Iwasawa invariants governing the growth of Selmer groups and class groups in a
$A(K)[l]\neq 0$, between Iwasawa invariants governing the growth of Selmer groups and class groups in a 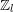 $\mathbb{Z}_{l}$-extension.
$\mathbb{Z}_{l}$-extension.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © The Author 2014
References
- 4
- Cited by


