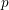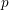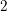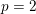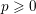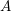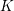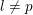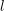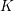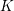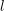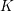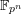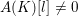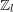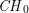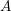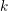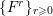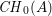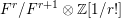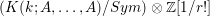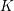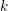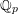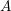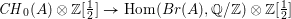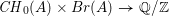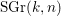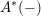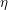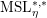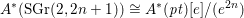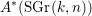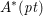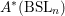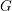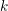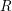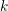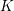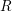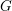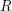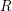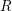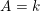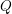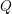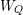Dedicated to Ragnar-Olaf Buchweitz on the occasion of his 60th birthday
Research Article
Level 1 Hecke algebras of modular forms modulo
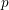 $p$
$p$
- Part of:
-
- Published online by Cambridge University Press:
- 27 November 2014, pp. 397-415
-
- Article
-
- You have access
- Export citation
Selmer groups and class groups
- Part of:
-
- Published online by Cambridge University Press:
- 11 November 2014, pp. 416-434
-
- Article
-
- You have access
- Export citation
On a filtration of
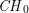 $\mathit{CH}_{0}$ for an abelian variety
$\mathit{CH}_{0}$ for an abelian variety
- Part of:
-
- Published online by Cambridge University Press:
- 22 December 2014, pp. 435-460
-
- Article
-
- You have access
- Export citation
The special linear version of the projective bundle theorem
- Part of:
-
- Published online by Cambridge University Press:
- 07 November 2014, pp. 461-501
-
- Article
-
- You have access
- Export citation
Frobenius categories, Gorenstein algebras and rational surface singularities
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2014, pp. 502-534
-
- Article
-
- You have access
- Export citation
On Grothendieck–Serre’s conjecture concerning principal
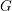 $G$-bundles over reductive group schemes: I
$G$-bundles over reductive group schemes: I
- Part of:
-
- Published online by Cambridge University Press:
- 28 October 2014, pp. 535-567
-
- Article
-
- You have access
- Export citation
Quotient closed subcategories of quiver representations
- Part of:
-
- Published online by Cambridge University Press:
- 15 October 2014, pp. 568-602
-
- Article
-
- You have access
- Export citation
Front Cover (OFC, IFC) and matter
COM volume 151 Issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 13 March 2015, pp. f1-f4
-
- Article
-
- You have access
- Export citation
Back Cover (OBC, IBC) and matter
COM volume 151 Issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 13 March 2015, pp. b1-b2
-
- Article
-
- You have access
- Export citation