Skip to main content Accessibility help

We use cookies to distinguish you from other users and to provide you with a better experience on our websites. Close this message to accept cookies or find out how to manage your cookie settings.

Close cookie message
×
Home
  • Home
EnglishFrançais
Compositio Mathematica Compositio Mathematica

Article contents

Quotient closed subcategories of quiver representations

Part of: Algebraic combinatorics Representation theory of rings and algebras

Published online by Cambridge University Press:  15 October 2014

Steffen Oppermann ,
Idun Reiten  and
Hugh Thomas
Steffen Oppermann
Affiliation:
Department of Mathematics, NTNU, Trondheim, Norway email steffen.oppermann@math.ntnu.no
Idun Reiten
Affiliation:
Department of Mathematics, NTNU, Trondheim, Norway email idunr@math.ntnu.no
Hugh Thomas
Affiliation:
Department of Mathematics and Statistics, UNB, PO Box 4400, Fredericton, Canada email hugh@math.unb.ca
Corresponding
E-mail address:
steffen.oppermann@math.ntnu.no
idunr@math.ntnu.no
hugh@math.unb.ca
Save pdf (0.56 mb)
Rights & Permissions[Opens in a new window]

Abstract

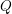Let $Q$ be a finite quiver without oriented cycles, and let 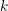$k$ be an algebraically closed field. The main result in this paper is that there is a natural bijection between the elements in the associated Weyl group 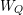$W_{Q}$ and the cofinite additive quotient closed subcategories of the category of finite dimensional right modules over 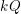$kQ$ . We prove this correspondence by linking these subcategories to certain ideals in the preprojective algebra associated to 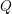$Q$ , which are also indexed by elements of 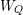$W_{Q}$ .

Keywords

quotient closed subcategories Weyl groups preprojective algebras sorting order

MSC classification

Primary: 16G20: Representations of quivers and partially ordered sets 16G70: Auslander-Reiten sequences (almost split sequences) and Auslander-Reiten quivers 05E10: Combinatorial aspects of representation theory
Type
Research Article
Information
Compositio Mathematica , Volume 151 , Issue 3 , March 2015 , pp. 568 - 602
Copyright
© The Author(s) 2014 

References

Amiot, C., Iyama, O., Reiten, I. and Todorov, G., Preprojective algebras and c-sortable words, Proc. Lond. Math. Soc. (3) 104 (2012), 513–539.CrossRefGoogle Scholar
Armstrong, D., The sorting order on a Coxeter group, J. Combin. Th. Series A 116 (2009), 1285–1305.CrossRefGoogle Scholar
Auslander, M., Platzeck, M. I. and Reiten, I., Coxeter functors without diagrams, Trans. Amer. Math. Soc. 250 (1979), 1–46.CrossRefGoogle Scholar
Auslander, M. and Solberg, Ø., Relative homology and representation theory I-III, Comm. Algebra 21 (1993), 2995–3097.CrossRefGoogle Scholar
Baer, D., Geigle, W. and Lenzing, H., The preprojective algebra of a tame hereditary algebra, Comm. Algebra 15 (1987), 425–457.CrossRefGoogle Scholar
Baumann, P. and Kamnitzer, J., Preprojective algebras and MV polytopes, Represent. Theory 16 (2012), 152–188.CrossRefGoogle Scholar
Bernšteĭn, I. N., Gel’fand, I. M. and Ponomarev, V. A., Coxeter functors, and Gabriel’s theorem, Uspekhi Mat. Nauk 28 (1973), 19–33 (in Russian).Google Scholar
Björner, A. and Brenti, F., Combinatorics of Coxeter groups, Graduate Texts in Mathematics, vol. 231 (Springer, New York, 2005).Google Scholar
Buan, A. B., Iyama, O., Reiten, I. and Scott, J., Cluster structures for 2-Calabi–Yau categories and unipotent groups, Compositio Math. 145 (2009), 1035–1079.CrossRefGoogle Scholar
Cartan, H. and Eilenberg, S., Homological algebra (Princeton University Press, Princeton, NJ, 1956).Google Scholar
Deng, B., Du, J., Parshall, B. and Wang, J., Finite dimensional algebras and quantum groups, Mathematical Surveys and Monographs, vol. 150 (American Mathematical Society, Providence, RI, 2008).CrossRefGoogle Scholar
Geiß, Ch., Leclerc, B. and Schröer, J., Semicanonical bases and preprojective algebras. II. A multiplication formula, Compositio Math. 143 (2007), 1313–1334.CrossRefGoogle Scholar
Ingalls, C. and Thomas, H., Noncrossing partitions and representations of quivers, Compositio Math. 145 (2009), 1533–1562.CrossRefGoogle Scholar
Iyama, O. and Reiten, I., Fomin–Zelevinsky mutation and tilting modules over Calabi–Yau algebras, Amer. J. Math. 130 (2008), 1087–1149.CrossRefGoogle Scholar
Krause, H. and Prest, M., The Gabriel–Roiter filtration of the Ziegler spectrum, Q. J. Math. 64 (2013), 891–901.CrossRefGoogle Scholar
Lam, T. and Pylyavskyy, P., Total positivity for loop groups II: Chevalley generators, Transform. Groups 18 (2013), 179–231.CrossRefGoogle Scholar
Lam, T. and Williams, L., Total positivity for cominuscule Grassmannians, New York J. Math. 14 (2008), 53–99.Google Scholar
Pilaud, V. and Stump, C., Brick polytopes of spherical subword complexes: A new approach to generalized associahedra, Preprint (2011), arXiv:1111.3349.Google Scholar
Postnikov, A., Total positivity, Grassmannians, and networks, Preprint (2006),arXiv:math/0609764.Google Scholar
Reading, N., Clusters, Coxeter-sortable elements and noncrossing partitions, Trans. Amer. Math. Soc. 359 (2007), 5931–5958.CrossRefGoogle Scholar
Reading, N., Sortable elements and Cambrian lattices, Algebra Universalis 56 (2007), 411–437.CrossRefGoogle Scholar
Ringel, C., The preprojective algebra of a quiver, in Algebras and Modules II, Can. Math. Soc. Conf. Proc., 24 (1998), 467–480.Google Scholar
Ringel, C., Minimal infinite submodule-closed subcategories, Bull. Sci. Math. 136 (2012), 820–830.CrossRefGoogle Scholar
Stembridge, J., Folding by automorphisms, Preprint (2008); available at math.lsa.umich.edu/∼jrs/papers/folding.ps.gz.Google Scholar

Altmetric attention score

Full text views

Full text views reflects PDF downloads, PDFs sent to Google Drive, Dropbox and Kindle and HTML full text views.

Total number of HTML views: 0
Total number of PDF views: 77 *
View data table for this chart

* Views captured on Cambridge Core between September 2016 - 23rd January 2021. This data will be updated every 24 hours.

Access
7 Cited by
Hostname: page-component-76cb886bbf-tmbpq Total loading time: 0.838 Render date: 2021-01-23T15:43:50.140Z Query parameters: { "hasAccess": "1", "openAccess": "0", "isLogged": "0", "lang": "en" } Feature Flags: { "shouldUseShareProductTool": true, "shouldUseHypothesis": true, "isUnsiloEnabled": true, "metricsAbstractViews": false, "figures": false, "newCiteModal": false }

Send article to Kindle

To send this article to your Kindle, first ensure no-reply@cambridge.org is added to your Approved Personal Document E-mail List under your Personal Document Settings on the Manage Your Content and Devices page of your Amazon account. Then enter the ‘name’ part of your Kindle email address below. Find out more about sending to your Kindle. Find out more about sending to your Kindle.

Note you can select to send to either the @free.kindle.com or @kindle.com variations. ‘@free.kindle.com’ emails are free but can only be sent to your device when it is connected to wi-fi. ‘@kindle.com’ emails can be delivered even when you are not connected to wi-fi, but note that service fees apply.

Find out more about the Kindle Personal Document Service.

Quotient closed subcategories of quiver representations
Available formats
×

Send article to Dropbox

To send this article to your Dropbox account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Dropbox.

Quotient closed subcategories of quiver representations
Available formats
×

Send article to Google Drive

To send this article to your Google Drive account, please select one or more formats and confirm that you agree to abide by our usage policies. If this is the first time you use this feature, you will be asked to authorise Cambridge Core to connect with your <service> account. Find out more about sending content to Google Drive.

Quotient closed subcategories of quiver representations
Available formats
×
×

Reply to: Submit a response

Your details

Conflicting interests

Do you have any conflicting interests? *