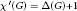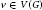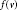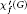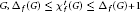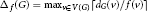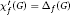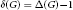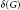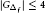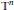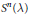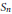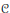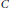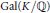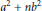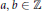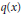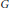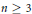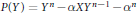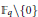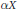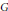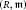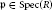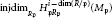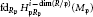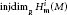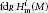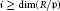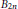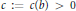Research Article
Diophantine Approximation for Certain Algebraic Formal Power Series in Positive Characteristic
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 673-683
-
- Article
-
- You have access
- Export citation
The f-Chromatic Index of a Graph Whose f-Core Has Maximum Degree 2
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 449-458
-
- Article
-
- You have access
- Export citation
Semiclassical Limits of Eigenfunctions on Flat n-Dimensional Tori
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 3-12
-
- Article
-
- You have access
- Export citation
On the Notion of Visibility of Torsors
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-228
-
- Article
-
- You have access
- Export citation
Ordering the Representations of
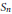 ${{S}_{n}}$ Using the Interchange Process
${{S}_{n}}$ Using the Interchange Process
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 13-30
-
- Article
-
- You have access
- Export citation
Cesàro Operators on the Hardy Spaces of the Half-Plane
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 229-240
-
- Article
-
- You have access
- Export citation
Envelope Dimension of Modules and the Simplified Radical Formula
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 683-694
-
- Article
-
- You have access
- Export citation
On Certain Multivariable Subnormal Weighted Shifts and their Duals
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 459-465
-
- Article
-
- You have access
- Export citation
Derivations and Valuation Rings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 31-38
-
- Article
-
- You have access
- Export citation
Inclusion Relations for New Function Spaces on Riemann Surfaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 466-476
-
- Article
-
- You have access
- Export citation
Versions of Schwarz's Lemma for Condenser Capacity and Inner Radius
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 241-250
-
- Article
-
- You have access
- Export citation
Carmichael Meets Chebotarev
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 695-708
-
- Article
-
- You have access
- Export citation
Sign Changes of the Liouville Function on Quadratics
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 251-257
-
- Article
-
- You have access
- Export citation
Hypercyclic Abelian Groups of Affine Maps on ℂn
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 477-490
-
- Article
-
- You have access
- Export citation
Comparison Theorem for Conjugate Points of a Fourth-order Linear Differential Equation
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 39-43
-
- Article
-
- You have access
- Export citation
Universal Minimal Flows of Groups of Automorphisms of Uncountable Structures
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 709-722
-
- Article
-
- You have access
- Export citation
The Smallest Pisot Element in the Field of Formal Power Series Over a Finite Field
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 258-264
-
- Article
-
- You have access
- Export citation
Polystable Parabolic Principal G-Bundles and Hermitian-Einstein Connections
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 44-54
-
- Article
-
- You have access
- Export citation
A Note on Homological Dimensions of Artinian Local Cohomology Modules
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 491-499
-
- Article
-
- You have access
- Export citation
On the Sum of Digits of Numerators of Bernoulli Numbers
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 723-728
-
- Article
-
- You have access
- Export citation