No CrossRef data available.
Article contents
Diophantine Approximation for CertainAlgebraic Formal Power Series in PositiveCharacteristic
Published online by Cambridge University Press: 20 November 2018
Abstract.
In this paper, we study rational approximations for certain algebraic power series over a finite field. We obtain results for irrational elements of strictly positive degree satisfying an equation of the type
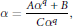 $$\alpha =\frac{A{{\alpha }^{q}}+B}{C{{\alpha }^{q}}},$$
$$\alpha =\frac{A{{\alpha }^{q}}+B}{C{{\alpha }^{q}}},$$
where 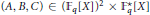 $\left( A,B,C \right)\,\in \,{{\left( {{\mathbb{F}}_{q}}\left[ X \right] \right)}^{2}}\times \mathbb{F}_{q}^{*}\left[ X \right]$. In particular, under some conditions on the polynomials
$\left( A,B,C \right)\,\in \,{{\left( {{\mathbb{F}}_{q}}\left[ X \right] \right)}^{2}}\times \mathbb{F}_{q}^{*}\left[ X \right]$. In particular, under some conditions on the polynomials 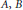 $A,\,B$ and
$A,\,B$ and 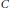 $C$, we will give well approximated elements satisfying this equation.
$C$, we will give well approximated elements satisfying this equation.
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013




