Article contents
Ordering the Representations of 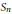 ${{S}_{n}}$ Using the Interchange Process
${{S}_{n}}$ Using the Interchange Process
Published online by Cambridge University Press: 20 November 2018
Abstract
Inspired by Aldous' conjecture for the spectral gap of the interchange process and its recent resolution by Caputo, Liggett, and Richthammer, we define an associated order 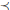 $\prec $ on the irreducible representations of
$\prec $ on the irreducible representations of 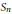 ${{S}_{n}}$. Aldous' conjecture is equivalent to certain representations being comparable in this order, and hence determining the “Aldous order” completely is a generalized question. We show a few additional entries for this order.
${{S}_{n}}$. Aldous' conjecture is equivalent to certain representations being comparable in this order, and hence determining the “Aldous order” completely is a generalized question. We show a few additional entries for this order.
Keywords
- Type
- Research Article
- Information
- Copyright
- Copyright © Canadian Mathematical Society 2013
References
- 1
- Cited by


