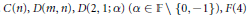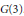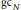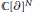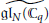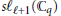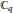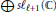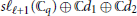Research Article
Coordinatization Theorems For Graded Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 451-465
-
- Article
-
- You have access
- Export citation
Award Winners
Research Article
A Note on the Automorphic Langlands Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 466-482
-
- Article
-
- You have access
- Export citation
Research Article
Diffraction of Weighted Lattice Subsets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 483-498
-
- Article
-
- You have access
- Export citation
Group Gradings on Matrix Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 499-508
-
- Article
-
- You have access
- Export citation
Lie Superalgebras Graded by the Root Systems C(n), D(m, n), D(2, 1, α), F(4), G(3)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 509-524
-
- Article
-
- You have access
- Export citation
Some Factorizations in Universal Enveloping Algebras of Three Dimensional Lie Algebras and Generalizations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 525-536
-
- Article
-
- You have access
- Export citation
Polytopal Realizations of Generalized Associahedra
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 537-566
-
- Article
-
- You have access
- Export citation
Subalgebras of gcN and Jacobi Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 567-605
-
- Article
-
- You have access
- Export citation
Postcards from the Edge, or Snapshots of the Theory of Generalised Moonshine
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 606-622
-
- Article
-
- You have access
- Export citation
Fermionic and Bosonic Representations of the Extended Affine Lie Algebra
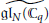 $\widetilde{\mathfrak{g}{{\mathfrak{l}}_{N}}\left( {{\mathbb{C}}_{q}} \right)}$
$\widetilde{\mathfrak{g}{{\mathfrak{l}}_{N}}\left( {{\mathbb{C}}_{q}} \right)}$
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 623-633
-
- Article
-
- You have access
- Export citation
Local Complexity of Delone Sets and Crystallinity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 634-652
-
- Article
-
- You have access
- Export citation
Specializations of Jordan Superalgebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 653-671
-
- Article
-
- You have access
- Export citation
A New Class of Representations of EALA Coordinated by Quantum Tori in Two Variables
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 672-685
-
- Article
-
- You have access
- Export citation
An Aspect of Icosahedral Symmetry
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 686-696
-
- Article
-
- You have access
- Export citation
Pure Discrete Spectrum for One-dimensional Substitution Systems of Pisot Type
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 697-710
-
- Article
-
- You have access
- Export citation
Classification of Quantum Tori with Involution
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 711-731
-
- Article
-
- You have access
- Export citation
Other
Index of Volume 45
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 732-736
-
- Article
-
- You have access
- Export citation