Hostname: page-component-848d4c4894-8bljj Total loading time: 0 Render date: 2024-07-06T09:48:29.843Z Has data issue: false hasContentIssue false
  • English
  • Français

Diffraction of Weighted Lattice Subsets

Published online by Cambridge University Press:  20 November 2018

Michael Baake
Michael Baake*
Affiliation:
Institut für Mathematik Universität Greifswald Jahnstr. 15a 17487 Greifswald Germany, email: mbaake@uni-greifswald.de
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

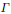A Dirac comb of point measures in Euclidean space with bounded complex weights that is supported on a lattice $\Gamma$ inherits certain general properties from the lattice structure. In particular, its autocorrelation admits a factorization into a continuous function and the uniformlattice Dirac comb, and its diffraction measure is periodic, with the dual lattice 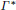${{\Gamma }^{*}}$ as lattice of periods. This statement remains true in the setting of a locally compact Abelian group whose topology has a countable base.

Keywords

52C0743A2552C2343A05diffractionDirac combslattice subsetshomometric sets
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 483 - 498
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Argabright, L. and de Lamadrid, J. Gil, Fourier Analysis of Unbounded Measures on Locally Compact Abelian Groups. Mem. Amer.Math. Soc. 145, Providence, Rhode Island, 1974.Google Scholar
[2] Baake, M. and Höffe, M., Diffraction of random tilings: some rigorous results. J. Statist. Phys. 99 (2000), 219–261; math-ph/9904005.Google Scholar
[3] Baake, M. and Moody, R. V., Self-similar measures for quasicrystals. In: Directions in Mathematical Quasicrystals (eds. M. Baake and R. V. Moody), CRM Monograph Series 13, Amer. Math. Soc., Providence, Rhode Island, (2000), 1–42; math.MG/0008063.Google Scholar
[4] Baake, M. and Moody, R. V., Weighted Dirac combs with pure point diffraction. Preprint, math.MG/0203030.Google Scholar
[5] Baake, M., Moody, R. V. and Pleasants, P. A. B., Diffraction from visible lattice points and k-th power free integers. Discrete Math. 221 (2000), 3–42; math.MG/9906132.Google Scholar
[6] Baake, M., Moody, R. V. and Schlottmann, M., Limit-(quasi)periodic point sets as quasicrystals with p-adic internal spaces. J. Phys. A 31 (1998), 5755–5765; math-ph/9901008.Google Scholar
[7] Berg, C. and Forst, G., Potential Theory on Locally Compact Abelian Groups. Springer, Berlin, 1975.Google Scholar
[8] Bourbaki, N., Elements of Mathematics: General Topology. Ch. 1–4 and Ch. 5–10, reprint, Springer, Berlin, 1989.Google Scholar
[9] Córdoba, A., Dirac combs. Lett. Math. Phys. 17 (1989), 191–196.Google Scholar
[10] Cowley, J. M., Diffraction Physics. 3rd edition, North-Holland, Amsterdam, 1995.Google Scholar
[11] Gurarii, V. P., Group Methods in Commutative Harmonic Analysis. Published as: Commutative Harmonic Analysis II (eds. V. P. Havin and N. K. Nikolski), EMS 25, Springer, Berlin, 1998.Google Scholar
[12] Höffe, M., Diffraction of the dart-rhombus random tiling. Math. Sci. Engrg. (A) 294.296 (2000), 373–376; math-ph/9911014.Google Scholar
[13] Höffe, M. and Baake, M., Surprises in diffuse scattering. Z. Krist. 215 (2000), 441–444; math-ph/0004022.Google Scholar
[14] Hof, A., On diffraction by aperiodic structures. Commun.Math. Phys. 169 (1995), 25–43.Google Scholar
[15] Hof, A., Diffraction of aperiodic structures at high temperatures. J. Phys. A 28 (1995), 57–62.Google Scholar
[16] Kendall, D. G. and Rankin, R. A., On the number of points of a given lattice in a random hypersphere. Quart. J. Math. Oxford Ser. (2) 4 (1953), 178–89.Google Scholar
[17] Lagarias, J. C., Mathematical quasicrystals and the problem of diffraction. In: Directions in Mathematical Quasicrystals (eds. M. Baake and R. V. Moody), CRM Monograph Series 13, Amer. Math. Soc., Providence, Rhode Island, 2000, 61–93.Google Scholar
[18] Lang, S., Real and Functional Analysis. 3rd edition, Graduate Texts in Math. 142, Springer, New York, 1993.Google Scholar
[19] Lee, J.-Y. and Moody, R. V., Lattice substitution systems and model sets. Discrete Comput. Geom. 25 (2001), 173–201; math.MG/0002019.Google Scholar
[20] Lee, J.-Y., Moody, R. V. and Solomyak, B., Pure point dynamical and diffraction spectrum. Preprint, mp arc/02-39, to appear in Ann. Inst. H. Poincaré; Consequences of pure point diffraction spectra for multiset substitution systems. Preprint, 2002.Google Scholar
[21] Patterson, A. L., Ambiguities in the X-ray analysis of crystal structures. Phys. Rev. 65 (1944), 195–201.Google Scholar
[22] von Querenburg, B., Mengentheoretische Topologie. 2nd edition, Springer, Berlin, 1979.Google Scholar
[23] Reed, M. and Simon, B., Methods of Modern Mathematical Physics. I: Functional Analysis. 2nd edition, Academic Press, San Diego, California, 1980.Google Scholar
[24] Rosenblatt, J. and Seymour, P. D., The structure of homometric sets. SIAM J. Algebraic Discrete Methods 3 (1982), 343–350.Google Scholar
[25] Rudin, W., Functional Analysis. 2nd edition, McGraw-Hill, New York, 1991.Google Scholar
[26] Schlottmann, M., Generalized model sets and dynamical systems. In: Directions in Mathematical Quasicrystals (eds. M. Baake and R. V. Moody), CRM Monograph Series 13, Amer. Math. Soc., Providence, Rhode Island, (2000), 143–159.Google Scholar
[27] Welberry, T. R., Diffuse X-ray scattering and models of disorder. Rep. Progr. Phys. 48 (1985), 1543–1593.Google Scholar