Hostname: page-component-848d4c4894-r5zm4 Total loading time: 0 Render date: 2024-07-06T09:13:36.854Z Has data issue: false hasContentIssue false
  • English
  • Français

Group Gradings on Matrix Algebras

Published online by Cambridge University Press:  20 November 2018

Yu. A. Bahturin  and
M. V. Zaicev
Yu. A. Bahturin
Affiliation:
Department of Mathematics and Statistics Memorial University of Newfoundland St. John's, NF A1A 5K9 and Department of Algebra Faculty of Mathematics and Mechanics Moscow State University Moscow 119899 Russia, email: yuri@math.mun.ca
M. V. Zaicev
Affiliation:
Department of Algebra Faculty of Mathematics and Mechanics Moscow State University Moscow 119899 Russia, email: zaicev@mech.math.msu.su
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

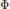Let $\Phi $ be an algebraically closed field of characteristic zero, 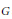$G$ a finite, not necessarily abelian, group. Given a 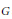$G$-grading on the full matrix algebra 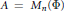$A\,=\,{{M}_{n}}\left( \Phi \right)$, we decompose 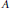$A$ as the tensor product of graded subalgebras 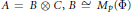$A\,=\,B\,\otimes \,C,\,B\,\cong \,{{M}_{p}}\left( \Phi \right)$ being a graded division algebra, while the grading of 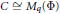$C\,\cong \,{{M}_{q}}\left( \Phi \right)$ is determined by that of the vector space 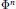${{\Phi }^{n}}$. Now the grading of 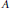$A$ is recovered from those of 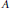$A$ and $B$ using a canonical “induction” procedure.

Keywords

16W50
Type
Research Article
Information
Canadian Mathematical Bulletin , Volume 45 , Issue 4 , 01 December 2002 , pp. 499 - 508
Copyright
Copyright © Canadian Mathematical Society 2002

References

[1] Bahturin, Yu. A., Zaicev, M. V. and Sehgal, S. K., Group Gradings on Associative Algebras. J. Algebra 241 (2001), 677–698.Google Scholar
[2] Curtis, C. W. and Reiner, I., Representation Theory of Finite Groups and Associative Algebras. John Wiley, New York, London, 1962.Google Scholar
[3] Dăascăalescu, S., Ion, B., Năastăasescu, C. and Rios Montes, J., Group gradings on full matrix rings. J. Algebra 220 (1999), 709–728.Google Scholar
[4] Elduque, A., Gradings on Octonions. J. Algebra 207 (1998), 342–354.Google Scholar
[5] Havliăcek, Miloslav, Patera, Jiări and Pelantova, Edita, On Lie gradings. III. Gradings of the real forms of classical Lie algebras. Linear Algebra Appl. (1–3) 314 (2000), 1–47.Google Scholar
[6] Hwang, Y.-S. and Wadsworth, A. R., Correspondences between valued division algebras and graded division algebras. J. Algebra 220 (1999), 73–114.Google Scholar
[7] Jacobson, N., The theory of rings. Amer.Math. Soc. Math. Surveys 1, Amer. Math. Soc., New York, 1943.Google Scholar
[8] Kantor, I. L., Some generalizations of Jordan algebras. Trudy Sem. Vektor. Tenzor. Anal. 16 (1972), 407–499.Google Scholar
[9] Montgomery, S., Hopf Algebras and Their Actions on Rings. CBMS Reg. Conf. Ser. in Math. 82, Amer.Math. Soc., Providence, RI, 1993.Google Scholar
[10] Năastăasescu, C. and van Oystaeyen, F., Graded ring theory. North-Holland Mathematical Library 28, North-Holland Publishing Co., Amsterdam-New York, 1982.Google Scholar
[11] Sehgal, S. K., Topics in Group Rings. Marcel Dekker, New York, 1978.Google Scholar
[12] Smirnov, O. N., Simple associative algebras with finite Z-grading. J. Algebra 196 (1997), 171–184.Google Scholar
[13] Smirnov, O. N., Finite Z-grading on Lie algebras and symplectic involution. J. Algebra 218 (1999), 246–275.Google Scholar
[14] Zaicev, M. V. and Sehgal, S. K., Finite gradings on simple Artinian rings. Vestnik Moskov. Univ.Mat. Mekh. (3) 2001, 21–24.Google Scholar