Research Article
On Integer Matrices and Incidence Matrices of Certain Combinatorial Configurations, I: Square Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1-5
-
- Article
-
- You have access
- Export citation
On Integer Matrices and Incidence Matrices of Certain Combinatorial Configurations, II: Rectangular Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 6-8
-
- Article
-
- You have access
- Export citation
On Integer Matrices and Incidence Matrices of Certain Combinatorial Configurations, III: Rectangular Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 9-17
-
- Article
-
- You have access
- Export citation
Some Finitely Generated Analogues of a Group of A. H. Clifford
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 18-26
-
- Article
-
- You have access
- Export citation
A Fourier Formula for Series Summable (C, 1)
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 27-32
-
- Article
-
- You have access
- Export citation
On the Average Number of Trees in Certain Maps
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 33-41
-
- Article
-
- You have access
- Export citation
Determination of a Subset from Certain Combinatorial Properties
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 42-48
-
- Article
-
- You have access
- Export citation
Majorants in Variational Integration
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 49-74
-
- Article
-
- You have access
- Export citation
An Existence Theorem for Generalized Direct Products with Amalgamated Subgroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 75-82
-
- Article
-
- You have access
- Export citation
Remarks on Complementation in the Lattice of all Topologies
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 83-88
-
- Article
-
- You have access
- Export citation
The Lototsky Transform and Bernstein Polynomials
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 89-91
-
- Article
-
- You have access
- Export citation
Arithmetic Invariants of Subdivision of Complexes
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 92-96
-
- Article
-
- You have access
- Export citation
On Ingham's Summation Method
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 97-105
-
- Article
-
- You have access
- Export citation
The Representation of a Graph by Set Intersections
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 106-112
-
- Article
-
- You have access
- Export citation
Groups Associated with Certain Loci In [5]
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 113-119
-
- Article
-
- You have access
- Export citation
Principal Loop-Isotopes of Quasigroups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 120-125
-
- Article
-
- You have access
- Export citation
Term Rank of the Direct Product of Matrices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 126-138
-
- Article
-
- You have access
- Export citation
Classes of Functions on Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 139-146
-
- Article
-
- You have access
- Export citation
The Construction of Perfect and Extreme Forms
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 147-158
-
- Article
-
- You have access
- Export citation
A Weight Theory for Unitary Representations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 159-168
-
- Article
-
- You have access
- Export citation




 of characteristic different from 2 that satisfy: (i)
of characteristic different from 2 that satisfy: (i) 
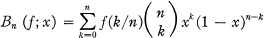
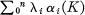 have the property that they are unaltered by all stellar subdivisions of
have the property that they are unaltered by all stellar subdivisions of 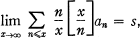
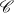 of certain pairs
of certain pairs 
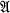 be a finite-dimensional linear associative algebra over the real field
be a finite-dimensional linear associative algebra over the real field 