Research Article
Degree One Maps and a Realization Theorem
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 769-796
-
- Article
-
- You have access
- Export citation
Rings whose Indecomposable Injective Modules are Uniserial
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 797-805
-
- Article
-
- You have access
- Export citation
Ford and Dirichlet Regions for Fuchsian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 806-815
-
- Article
-
- You have access
- Export citation
Half-Turns and Infinite Chains of Clifford Configurations
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 816-831
-
- Article
-
- You have access
- Export citation
On Lucas-Sets for Vector-Valued Abstract Polynomials in K-inner Product Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 832-852
-
- Article
-
- You have access
- Export citation
Operateur de Stokes Dans des Espaces de Sobolev a Poids sur des Domaines Anguleux
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 853-882
-
- Article
-
- You have access
- Export citation
Spectral Inclusion and C.N.E.
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 883-887
-
- Article
-
- You have access
- Export citation
On a Problem of Turán about Polynomials HI
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 888-899
-
- Article
-
- You have access
- Export citation
L'Enveloppe Conjuguee D'Un Demi-Groupe Inverse a Metacentre Idempotent
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 900-909
-
- Article
-
- You have access
- Export citation
Isometries of Weighted Bergman Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 910-915
-
- Article
-
- You have access
- Export citation
Rearrangements that Preserve Rates of Divergence
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 916-920
-
- Article
-
- You have access
- Export citation
Intersection Patterns of Families of Convex Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 921-931
-
- Article
-
- You have access
- Export citation
On an Inequality of S. Bernstein
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 932-944
-
- Article
-
- You have access
- Export citation
Elements of Order Coxeter Number +1 in Chevalley Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 945-951
-
- Article
-
- You have access
- Export citation
Chromatic Solutions, II
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 952-960
-
- Article
-
- You have access
- Export citation
On Polynomials with Curved Majorants
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 961-968
-
- Article
-
- You have access
- Export citation
Class Numbers and Biquadratic Reciprocity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 969-988
-
- Article
-
- You have access
- Export citation
Symbole Holomorphe
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 989-995
-
- Article
-
- You have access
- Export citation
Brauer Groups, Class Groups and Maximal Orders for a Krull Scheme
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 996-1010
-
- Article
-
- You have access
- Export citation
Coefficients in Expansions of Certain Rational Functions
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 1011-1024
-
- Article
-
- You have access
- Export citation



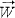 ,
,  ,
, 
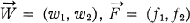 . Voici l'écriture matricielle de l'opérateur:
. Voici l'écriture matricielle de l'opérateur: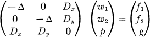
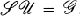 .
.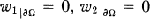 (Dirichlet); c'est donc ce probléme que nous étudions ici.
(Dirichlet); c'est donc ce probléme que nous étudions ici.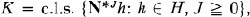
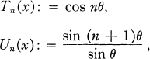
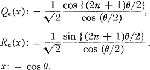
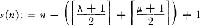
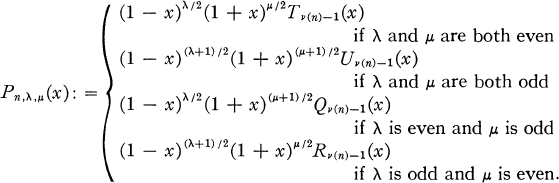
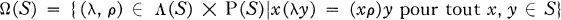
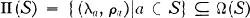
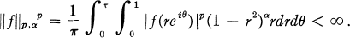
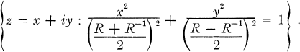
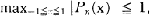
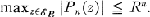
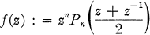
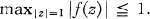
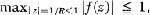

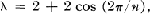

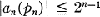
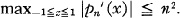
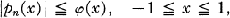
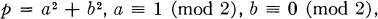
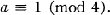
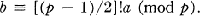
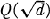 of discriminant
of discriminant 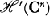 , nous montrons qu'il existe une fonction entière
, nous montrons qu'il existe une fonction entière 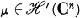 on ait
on ait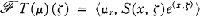
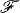 désigne la transformée de Fourier-Borel d'une fonctionnelle analytique). Une telle fonction
désigne la transformée de Fourier-Borel d'une fonctionnelle analytique). Une telle fonction 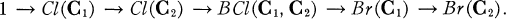
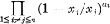
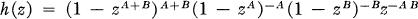
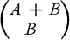 . Here, and throughout this paper,
. Here, and throughout this paper,