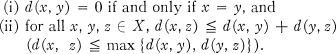Research Article
Some New Replaceable Translation Nets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 225-237
-
- Article
-
- You have access
- Export citation
On Rational Subdivisions of Polyhedra with Rational Vertices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 238-242
-
- Article
-
- You have access
- Export citation
Applications of Duality in the Theory of Finitely Generated Lattice-Ordered Abelian Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 243-254
-
- Article
-
- You have access
- Export citation
Kronecker Products and Local Joins of Graphs
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 255-269
-
- Article
-
- You have access
- Export citation
Multiplicative Functionals on Frechet Algebras with Bases
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 270-276
-
- Article
-
- You have access
- Export citation
Algebras with a Diagonable Subspace whose Centralizer Satisfies a Polynomial Identity
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 277-283
-
- Article
-
- You have access
- Export citation
Almost-P-Spaces
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 284-288
-
- Article
-
- You have access
- Export citation
Isomorphism of Some Simple 2-Graded Lie Algebras
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 289-294
-
- Article
-
- You have access
- Export citation
A Lebesgue Decomposition for Vector Valued Additive Set Functions Defined on a Lattice
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 295-298
-
- Article
-
- You have access
- Export citation
Generalized Bloch Mappings in Complex Hilbert Space
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 299-306
-
- Article
-
- You have access
- Export citation
An Analog of Nagata's Theorem for Modular LCM Domains
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 307-314
-
- Article
-
- You have access
- Export citation
When is a Matrix Sign Stable?
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 315-326
-
- Article
-
- You have access
- Export citation
Torsion Elements and the Classification of Vector Bundles
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 327-332
-
- Article
-
- You have access
- Export citation
Irreducible Automorphisms of Certain p-Groups
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 333-348
-
- Article
-
- You have access
- Export citation
Recursive Embeddings of Partial Orderings
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 349-359
-
- Article
-
- You have access
- Export citation
A Note on Quasi-Metrizability
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 360-366
-
- Article
-
- You have access
- Export citation
The 3-Irreducible Partially Ordered Sets
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 367-383
-
- Article
-
- You have access
- Export citation
Rigid Embedding of Simple Groups in the General Linear Group
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 384-391
-
- Article
-
- You have access
- Export citation
On Transformation and Oscillation of Linear Differential System
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 392-399
-
- Article
-
- You have access
- Export citation
Neighborly 4-Polytopes and Neighborly Combinatorial 3-Manifolds with Ten Vertices
-
- Published online by Cambridge University Press:
- 20 November 2018, pp. 400-420
-
- Article
-
- You have access
- Export citation



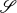 is a simplicial subdivision of
is a simplicial subdivision of 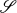
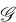 raph
raph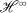 of bounded analytic functions. However, all Bloch functions are normal and therefore enjoy the “nice” properties of normal functions. The importance of the Bloch function concept is the combination of their richness as a family and their “nice” behavior.
of bounded analytic functions. However, all Bloch functions are normal and therefore enjoy the “nice” properties of normal functions. The importance of the Bloch function concept is the combination of their richness as a family and their “nice” behavior.
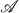 be a countable atomless Boolean algebra and let
be a countable atomless Boolean algebra and let 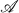 which is recursive in
which is recursive in 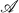 and which destroys all suprema and infima of
and which destroys all suprema and infima of