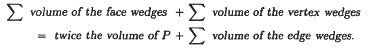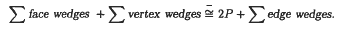Research Article
An uncertainty principle for the Dunkl transform
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 353-360
-
- Article
-
- You have access
- Export citation
The fixed point property for some uniformly nonoctahedral Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 361-367
-
- Article
-
- You have access
- Export citation
Lipschitz continuity of spectral measures
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 369-373
-
- Article
-
- You have access
- Export citation
Boundary two-parameter eight-state supersymmetric fermion model and Bethe ansatz solution
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 375-390
-
- Article
-
- You have access
- Export citation
Polytopes of roots of type AN
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 391-402
-
- Article
-
- You have access
- Export citation
Images of Hankel operators on the polydisk
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 403-408
-
- Article
-
- You have access
- Export citation
Two-transitive actions on conjugacy classes
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 409-420
-
- Article
-
- You have access
- Export citation
A note on the equation λ * ρ * μ = ρ
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 421-426
-
- Article
-
- You have access
- Export citation
Optimal weighted estimates for the Cauchy-Riemann equation on analytic polyhedra
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 427-431
-
- Article
-
- You have access
- Export citation
A fixed point theorem and its applications to a system of variational inequalities
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 433-442
-
- Article
-
- You have access
- Export citation
On copies of the null sequence Banach space in some vector measure spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 443-447
-
- Article
-
- You have access
- Export citation
Weak convergence of tensor products of vector measures with values in nuclear spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 449-458
-
- Article
-
- You have access
- Export citation
Subnormality conditions in non-torsion groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 459-465
-
- Article
-
- You have access
- Export citation
Note on U-closed semigroup rings
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 467-471
-
- Article
-
- You have access
- Export citation
Quasiprimitivity and quasigroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 473-475
-
- Article
-
- You have access
- Export citation
A note on Jeśmanowicz' conjecture concerning Pythagorean triples
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 477-480
-
- Article
-
- You have access
- Export citation
A KKM type theorem and its applications
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 481-493
-
- Article
-
- You have access
- Export citation
An Euler-type volume identity
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 495-508
-
- Article
-
- You have access
- Export citation
The second variation formula for exponentially harmonic maps
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 509-514
-
- Article
-
- You have access
- Export citation
Remarks on James's distortion theorems II
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 515-522
-
- Article
-
- You have access
- Export citation



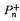 , of positive roots and the origin have been considered in relation to other branches of mathematics [4]. We show that exactly
, of positive roots and the origin have been considered in relation to other branches of mathematics [4]. We show that exactly 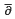 on analytic polyhedra. We provide an example to show why they cannot be improved.
on analytic polyhedra. We provide an example to show why they cannot be improved.