Hostname: page-component-8448b6f56d-jr42d Total loading time: 0 Render date: 2024-04-23T18:37:17.140Z Has data issue: false hasContentIssue false
  • English
  • Français

Polytopes of roots of type AN

Published online by Cambridge University Press:  17 April 2009

Soojin Cho
Soojin Cho
Affiliation:
ChungGu NaRae Apt. 102-901, ChunMin-Dong, Yusong-Gu, Taejon 305–390, Korea e-mail: sjcho@math.kaist.ac.kr
Rights & Permissions [Opens in a new window]

Abstract

Core share and HTML view are not available for this content. However, as you have access to this content, a full PDF is available via the ‘Save PDF’ action button.

Polytopes of roots of type An−1 are investigated, which we call Pn. The polytopes, 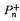, of positive roots and the origin have been considered in relation to other branches of mathematics [4]. We show that exactly n copies of 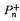forms a disjoint cover of Pn. Moreover, those n copies of 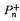can be obtained by letting the elements of a subgroup of the symmetric group Sn generated by an n-cycle act on 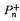. We also characterise the faces of Pn and some facets of 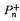, which we believe to be useful in some optimisation problems. As by-products, we obtain an interesting identity on the number of lattice paths and a triangulation of the product of two simplices.

Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 59 , Issue 3 , June 1999 , pp. 391 - 402
Copyright
Copyright © Australian Mathematical Society 1999

References

[1]Brøndsted, A., An introduction to convex polytopes, Graduate Texts in Mathematics 90 (Springer-Verlag, Berlin, Heidelberg, New York, 1983).Google Scholar
[2]Cho, S., ‘Minimal null designs and a density theorem of posets’, European J. Combin. 19 (1998), 433–440.Google Scholar
[3]Frankl, P. and Pach, J., ‘On the number of sets in a null t-design’, European J. Combin. 4 (1983), 21–23.Google Scholar
[4]Gelfand, I.M., Graev, M.I. and Postnikov, A., ‘Combinatorics of hypergeometric functions associated with positive roots’, in Arnold-Gelfand Mathematical Seminars 1993–1995 (Birkhäuser Boston, Boston, MA, 1997), pp. 205–221.Google Scholar
[5]Graham, R.L., Li, S.-Y. R. and Li, W.-C.W., ‘On the structure of t-designs’, SIAM J. Discrete Math. 1 (1980), 8–14.CrossRefGoogle Scholar
[6]Humphreys, J., Reflection groups and coxeter groups, Cambridge Studies in Advanced Mathematics 29 (Cambridge University Press, Cambridge, 1990).Google Scholar
[7]Liebler, R.A. and Zimmermann, K.H., ‘Combinatorial Sn-modules as codes’, J. Algebraic Combin. 4 (1995), 47–68.Google Scholar
[8]Onn, S., ‘Geometry, complexity, and combinatorics of permutation polytopes’, J. Combin. Theory Ser. A 64 (1993), 31–49.Google Scholar
[9]Sagan, B.E., The symmetric group. Representations, combinatorial algorithms and symmetric functions, Wadsworth & Brooks/Cole Mathematics Series (Wadsworth, Inc., Pacific Grove, CA, 1991).Google Scholar
[10]Ziegler, G.M., Lectures on Polytopes, Graduate Texts in Mathematics 152 (Springer-Verlag, Berlin, Heidelberg, New York, 1995).Google Scholar