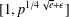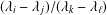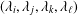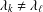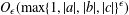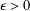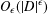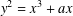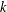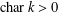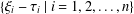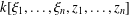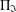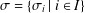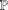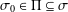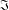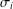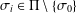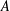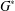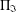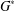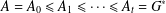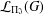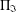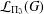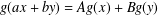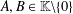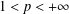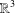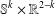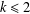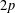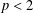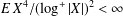Research Article
ON THE MINIMAL NUMBER OF SMALL ELEMENTS GENERATING FINITE PRIME FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 177-184
-
- Article
-
- You have access
- Export citation
ON POLYNOMIALS WHOSE ROOTS HAVE RATIONAL QUOTIENT OF DIFFERENCES
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2017, pp. 185-190
-
- Article
-
- You have access
- Export citation
A NOTE ON SCHMIDT’S CONJECTURE
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2017, pp. 191-195
-
- Article
-
- You have access
- Export citation
RAMIFICATION IN KUMMER EXTENSIONS ARISING FROM ALGEBRAIC TORI
- Part of:
-
- Published online by Cambridge University Press:
- 17 August 2017, pp. 196-204
-
- Article
-
- You have access
- Export citation
IMAGES OF HIGHER-ORDER DIFFERENTIAL OPERATORS OF POLYNOMIAL ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2017, pp. 205-211
-
- Article
-
- You have access
- Export citation
SUBSETS OF VERTICES GIVE MORITA EQUIVALENCES OF LEAVITT PATH ALGEBRAS
- Part of:
-
- Published online by Cambridge University Press:
- 30 March 2017, pp. 212-222
-
- Article
-
- You have access
- Export citation
LIE
 $n$-HIGHER DERIVATIONS AND LIE
$n$-HIGHER DERIVATIONS AND LIE  $n$-HIGHER DERIVABLE MAPPINGS
$n$-HIGHER DERIVABLE MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 09 June 2017, pp. 223-232
-
- Article
-
- You have access
- Export citation
ON THE LATTICE OF
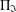 $\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-SUBNORMAL SUBGROUPS OF A FINITE GROUP
$\unicode[STIX]{x1D6F1}_{\mathfrak{I}}$-SUBNORMAL SUBGROUPS OF A FINITE GROUP
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 233-244
-
- Article
-
- You have access
- Export citation
STABLE, ALMOST STABLE AND ODD POINTS OF DYNAMICAL SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 26 April 2017, pp. 245-255
-
- Article
-
- You have access
- Export citation
ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2017, pp. 256-262
-
- Article
-
- You have access
- Export citation
A NOTE ON THE GENERALISED HYPERSTABILITY OF THE GENERAL LINEAR EQUATION
- Part of:
-
- Published online by Cambridge University Press:
- 29 August 2017, pp. 263-273
-
- Article
-
- You have access
- Export citation
EMBEDDINGS AND
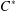 $C^{\ast }$-ENVELOPES OF EXACT OPERATOR SYSTEMS
$C^{\ast }$-ENVELOPES OF EXACT OPERATOR SYSTEMS
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 274-285
-
- Article
-
- You have access
- Export citation
THE ROLE OF DOMINATION AND SMOOTHING CONDITIONS IN THE THEORY OF EVENTUALLY POSITIVE SEMIGROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 286-298
-
- Article
-
- You have access
- Export citation
SHRINKING PROJECTION ALGORITHMS FOR THE SPLIT COMMON NULL POINT PROBLEM
- Part of:
-
- Published online by Cambridge University Press:
- 29 March 2017, pp. 299-306
-
- Article
-
- You have access
- Export citation
FIBONACCI–MANN ITERATION FOR MONOTONE ASYMPTOTICALLY NONEXPANSIVE MAPPINGS
- Part of:
-
- Published online by Cambridge University Press:
- 13 March 2017, pp. 307-316
-
- Article
-
- You have access
- Export citation
ON THE EXISTENCE OF
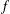 $f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
$f$-MAXIMAL SPACELIKE HYPERSURFACES IN CERTAIN WEIGHTED MANIFOLDS
- Part of:
-
- Published online by Cambridge University Press:
- 02 May 2017, pp. 317-325
-
- Article
-
- You have access
- Export citation
SELF-SHRINKERS WITH SECOND FUNDAMENTAL FORM OF CONSTANT LENGTH
- Part of:
-
- Published online by Cambridge University Press:
- 02 March 2017, pp. 326-332
-
- Article
-
- You have access
- Export citation
COMPLETE CONVERGENCE FOR ARRAYS AND THE LAW OF THE SINGLE LOGARITHM
- Part of:
-
- Published online by Cambridge University Press:
- 29 August 2017, pp. 333-344
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
POWER OF POSTS: A QUANTITATIVE ANALYSIS OF FACEBOOK ELECTION CAMPAIGNING INTERACTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2017, pp. 345-347
-
- Article
-
- You have access
- Export citation
NOVEL PREPROCESSING APPROACHES FOR OMICS DATA TYPES AND THEIR PERFORMANCE EVALUATION
- Part of:
-
- Published online by Cambridge University Press:
- 05 July 2017, pp. 348-349
-
- Article
-
- You have access
- Export citation