Article contents
ON CONVEX COMBINATIONS OF CONVEX HARMONIC MAPPINGS
Published online by Cambridge University Press: 07 August 2017
Abstract
The family 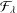 ${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ of orientation-preserving harmonic functions
${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ of orientation-preserving harmonic functions 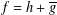 $f=h+\overline{g}$ in the unit disc
$f=h+\overline{g}$ in the unit disc 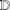 $\mathbb{D}$ (normalised in the standard way) satisfying
$\mathbb{D}$ (normalised in the standard way) satisfying  $$\begin{eqnarray}h^{\prime }(z)+g^{\prime }(z)=\frac{1}{(1+\unicode[STIX]{x1D706}z)(1+\overline{\unicode[STIX]{x1D706}}z)},\quad z\in \mathbb{D},\end{eqnarray}$$
$$\begin{eqnarray}h^{\prime }(z)+g^{\prime }(z)=\frac{1}{(1+\unicode[STIX]{x1D706}z)(1+\overline{\unicode[STIX]{x1D706}}z)},\quad z\in \mathbb{D},\end{eqnarray}$$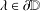 $\unicode[STIX]{x1D706}\in \unicode[STIX]{x2202}\mathbb{D}$, along with their rotations, play an important role among those functions that are harmonic and orientation-preserving and map the unit disc onto a convex domain. The main theorem in this paper generalises results in recent literature by showing that convex combinations of functions in
$\unicode[STIX]{x1D706}\in \unicode[STIX]{x2202}\mathbb{D}$, along with their rotations, play an important role among those functions that are harmonic and orientation-preserving and map the unit disc onto a convex domain. The main theorem in this paper generalises results in recent literature by showing that convex combinations of functions in 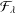 ${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ are convex.
${\mathcal{F}}_{\unicode[STIX]{x1D706}}$ are convex.
MSC classification
- Type
- Research Article
- Information
- Bulletin of the Australian Mathematical Society , Volume 96 , Issue 2 , October 2017 , pp. 256 - 262
- Copyright
- © 2017 Australian Mathematical Publishing Association Inc.
Footnotes
The second and third authors are supported by Fondecyt, Chile, grant 1150284. The third author is also partially supported by grant MTM2015-65792-P from MINECO/FEDER, the Thematic Research Network MTM2015-69323-REDT, MINECO, Spain, and the Academy of Finland, grant 268009.
References
- 6
- Cited by




