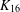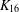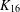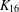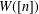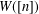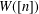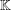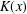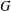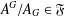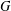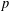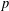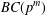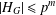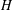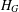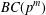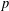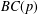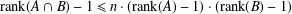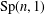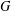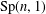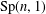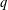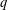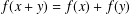Research Article
PERFECT 1-FACTORISATIONS OF
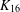 $K_{16}$
$K_{16}$
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2019, pp. 177-185
-
- Article
- Export citation
DEGREE OF THE
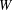 $W$-OPERATOR AND NONCROSSING PARTITIONS
$W$-OPERATOR AND NONCROSSING PARTITIONS
- Part of:
-
- Published online by Cambridge University Press:
- 23 October 2019, pp. 186-200
-
- Article
- Export citation
THE NUMBER OF CYCLIC SUBGROUPS OF FINITE ABELIAN GROUPS AND MENON’S IDENTITY
- Part of:
-
- Published online by Cambridge University Press:
- 17 May 2019, pp. 201-206
-
- Article
- Export citation
CLOSED FORMS FOR DEGENERATE BERNOULLI POLYNOMIALS
- Part of:
-
- Published online by Cambridge University Press:
- 10 January 2020, pp. 207-217
-
- Article
- Export citation
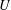 $U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
$U$-NUMBERS IN FIELDS OF FORMAL POWER SERIES OVER FINITE FIELDS
- Part of:
-
- Published online by Cambridge University Press:
- 29 July 2019, pp. 218-225
-
- Article
- Export citation
ON LITTLEWOOD’S PROOF OF THE PRIME NUMBER THEOREM
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2019, pp. 226-232
-
- Article
- Export citation
GENERALISATION OF A RESULT ON DISTINCT PARTITIONS WITH BOUNDED PART DIFFERENCES
- Part of:
-
- Published online by Cambridge University Press:
- 24 July 2019, pp. 233-237
-
- Article
- Export citation
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 09 July 2019, pp. 238-246
-
- Article
- Export citation
ON A LATTICE CHARACTERISATION OF FINITE SOLUBLE PST-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2019, pp. 247-254
-
- Article
- Export citation
FINITE
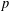 $p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
$p$-GROUPS ALL OF WHOSE NONNORMAL SUBGROUPS HAVE BOUNDED NORMAL CORES
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2019, pp. 255-265
-
- Article
- Export citation
INTERSECTIONS OF SUBGROUPS IN VIRTUALLY FREE GROUPS AND VIRTUALLY FREE PRODUCTS
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2019, pp. 266-271
-
- Article
- Export citation
CONJUGATING AUTOMORPHISMS OF GRAPH PRODUCTS: KAZHDAN’S PROPERTY (T) AND SQ-UNIVERSALITY
- Part of:
-
- Published online by Cambridge University Press:
- 07 August 2019, pp. 272-282
-
- Article
- Export citation
ON DISCRETENESS OF SUBGROUPS OF QUATERNIONIC HYPERBOLIC ISOMETRIES
- Part of:
-
- Published online by Cambridge University Press:
- 16 August 2019, pp. 283-293
-
- Article
- Export citation
A
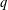 $q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
$q$-ANALOGUE OF A HYPERGEOMETRIC CONGRUENCE
- Part of:
-
- Published online by Cambridge University Press:
- 18 July 2019, pp. 294-298
-
- Article
- Export citation
ON APPROXIMATELY ADDITIVE MAPPINGS IN 2-BANACH SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 15 August 2019, pp. 299-310
-
- Article
- Export citation
EMBEDDINGS OF FREE TOPOLOGICAL VECTOR SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 20 August 2019, pp. 311-324
-
- Article
- Export citation
ON MODULATED TOPOLOGICAL VECTOR SPACES AND APPLICATIONS
- Part of:
-
- Published online by Cambridge University Press:
- 10 July 2019, pp. 325-332
-
- Article
- Export citation
ON ALMOST STABLE CMC HYPERSURFACES IN MANIFOLDS OF BOUNDED SECTIONAL CURVATURE
- Part of:
-
- Published online by Cambridge University Press:
- 10 September 2019, pp. 333-338
-
- Article
- Export citation
Abstracts of Australasian PhD Theses
THEORY AND STATISTICS OF LONG-RANGE DEPENDENT RANDOM PROCESSES
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 339-341
-
- Article
-
- You have access
- Export citation
THE PERFORMANCE OF SOME STATISTICAL PROCEDURES USED IN CASE-CONTROL STUDIES AND METHYLOMICS
- Part of:
-
- Published online by Cambridge University Press:
- 08 January 2020, pp. 342-344
-
- Article
-
- You have access
- Export citation