Article contents
ON THE EULER CHARACTERISTICS OF SIGNED SELMER GROUPS
Published online by Cambridge University Press: 09 July 2019
Abstract
Let 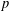 $p$ be an odd prime number and
$p$ be an odd prime number and  $E$ an elliptic curve defined over a number field
$E$ an elliptic curve defined over a number field 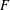 $F$ with good reduction at every prime of
$F$ with good reduction at every prime of 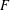 $F$ above
$F$ above 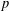 $p$. We compute the Euler characteristics of the signed Selmer groups of
$p$. We compute the Euler characteristics of the signed Selmer groups of 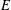 $E$ over the cyclotomic
$E$ over the cyclotomic 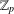 $\mathbb{Z}_{p}$-extension. The novelty of our result is that we allow the elliptic curve to have mixed reduction types for primes above
$\mathbb{Z}_{p}$-extension. The novelty of our result is that we allow the elliptic curve to have mixed reduction types for primes above 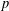 $p$ and mixed signs in the definition of the signed Selmer groups.
$p$ and mixed signs in the definition of the signed Selmer groups.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
M. F. Lim is supported by the National Natural Science Foundation of China under Grant Nos. 11550110172 and 11771164.
References
- 4
- Cited by




