Article contents
PERFECT 1-FACTORISATIONS OF 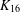 $K_{16}$
$K_{16}$
Published online by Cambridge University Press: 07 August 2019
Abstract
We report the results of a computer enumeration that found that there are 3155 perfect 1-factorisations (P1Fs) of the complete graph 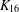 $K_{16}$. Of these, 89 have a nontrivial automorphism group (correcting an earlier claim of 88 by Meszka and Rosa [‘Perfect 1-factorisations of
$K_{16}$. Of these, 89 have a nontrivial automorphism group (correcting an earlier claim of 88 by Meszka and Rosa [‘Perfect 1-factorisations of 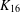 $K_{16}$ with nontrivial automorphism group’, J. Combin. Math. Combin. Comput. 47 (2003), 97–111]). We also (i) describe a new invariant which distinguishes between the P1Fs of
$K_{16}$ with nontrivial automorphism group’, J. Combin. Math. Combin. Comput. 47 (2003), 97–111]). We also (i) describe a new invariant which distinguishes between the P1Fs of 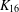 $K_{16}$, (ii) observe that the new P1Fs produce no atomic Latin squares of order 15 and (iii) record P1Fs for a number of large orders that exceed prime powers by one.
$K_{16}$, (ii) observe that the new P1Fs produce no atomic Latin squares of order 15 and (iii) record P1Fs for a number of large orders that exceed prime powers by one.
MSC classification
- Type
- Research Article
- Information
- Copyright
- © 2019 Australian Mathematical Publishing Association Inc.
Footnotes
Research supported by an Australian Government Research Training Program (RTP) Scholarship and by ARC grant DP150100506.
References
- 6
- Cited by


