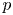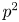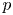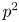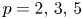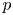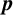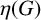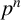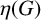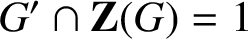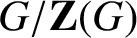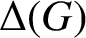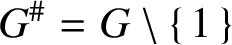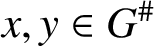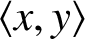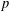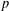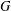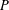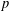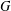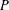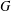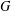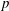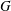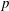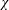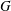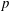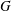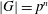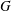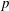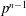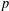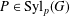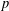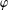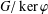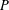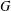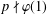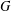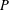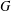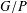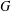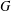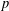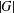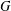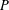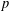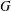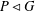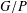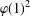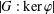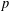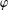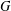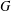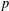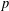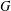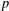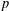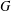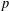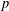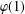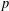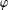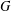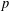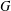50 results
FINITE SOLVABLE TIDY GROUPS ARE DETERMINED BY HALL SUBGROUPS WITH TWO PRIMES
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 109 / Issue 2 / April 2024
- Published online by Cambridge University Press:
- 27 July 2023, pp. 342-349
- Print publication:
- April 2024
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Three-dimensional food printing: its readiness for a food and nutrition insecure world
-
- Journal:
- Proceedings of the Nutrition Society / Volume 82 / Issue 4 / December 2023
- Published online by Cambridge University Press:
- 15 May 2023, pp. 468-477
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Cerebrospinal fluid neurofilament light predicts longitudinal diagnostic change in patients with psychiatric and neurodegenerative disorders
-
- Journal:
- Acta Neuropsychiatrica / Volume 36 / Issue 1 / February 2024
- Published online by Cambridge University Press:
- 28 April 2023, pp. 17-28
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
p-GROUPS WITH CYCLIC OR GENERALISED QUATERNION HUGHES SUBGROUPS: CLASSIFYING TIDY p-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 108 / Issue 3 / December 2023
- Published online by Cambridge University Press:
- 20 April 2023, pp. 443-448
- Print publication:
- December 2023
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Toward a classification of the supercharacter theories of Cp × Cp
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 65 / Issue 4 / November 2022
- Published online by Cambridge University Press:
- 12 October 2022, pp. 990-1010
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
CONJUGACY CLASSES OF MAXIMAL CYCLIC SUBGROUPS AND NILPOTENCE CLASS OF
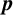 $\boldsymbol {p}$
-GROUPS
$\boldsymbol {p}$
-GROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 106 / Issue 3 / December 2022
- Published online by Cambridge University Press:
- 21 March 2022, pp. 463-469
- Print publication:
- December 2022
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTENDING RESULTS OF MORGAN AND PARKER ABOUT COMMUTING GRAPHS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 105 / Issue 1 / February 2022
- Published online by Cambridge University Press:
- 11 May 2021, pp. 92-100
- Print publication:
- February 2022
-
- Article
- Export citation
A history of high-power laser research and development in the United Kingdom
- Part of
-
- Journal:
- High Power Laser Science and Engineering / Volume 9 / 2021
- Published online by Cambridge University Press:
- 27 April 2021, e18
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
THE CYCLIC GRAPH OF A Z-GROUP
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 104 / Issue 2 / October 2021
- Published online by Cambridge University Press:
- 14 December 2020, pp. 295-301
- Print publication:
- October 2021
-
- Article
- Export citation
On solvable groups with one vanishing class size
- Part of
-
- Journal:
- Proceedings of the Royal Society of Edinburgh. Section A: Mathematics / Volume 151 / Issue 5 / October 2021
- Published online by Cambridge University Press:
- 14 September 2020, pp. 1467-1486
- Print publication:
- October 2021
-
- Article
- Export citation
Modeling protoplanetary disk evolution in young star forming regions
-
- Journal:
- Proceedings of the International Astronomical Union / Volume 16 / Issue S362 / June 2020
- Published online by Cambridge University Press:
- 20 January 2023, pp. 300-305
- Print publication:
- June 2020
-
- Article
-
- You have access
- Open access
- Export citation
Enumerating isoclinism classes of semi-extraspecial groups
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 63 / Issue 2 / May 2020
- Published online by Cambridge University Press:
- 24 February 2020, pp. 426-442
-
- Article
- Export citation
DEGREES OF BRAUER CHARACTERS AND NORMAL SYLOW
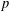 $p$-SUBGROUPS
$p$-SUBGROUPS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 102 / Issue 2 / October 2020
- Published online by Cambridge University Press:
- 08 January 2020, pp. 237-239
- Print publication:
- October 2020
-
- Article
- Export citation
Character Codegrees of Maximal Class
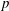 $p$-groups
$p$-groups
- Part of
-
- Journal:
- Canadian Mathematical Bulletin / Volume 63 / Issue 2 / June 2020
- Published online by Cambridge University Press:
- 25 September 2019, pp. 328-334
- Print publication:
- June 2020
-
- Article
- Export citation
MONOLITHIC BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 3 / December 2019
- Published online by Cambridge University Press:
- 28 March 2019, pp. 434-439
- Print publication:
- December 2019
-
- Article
- Export citation
SQUARES OF DEGREES OF BRAUER CHARACTERS AND MONOMIAL BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 100 / Issue 1 / August 2019
- Published online by Cambridge University Press:
- 29 January 2019, pp. 58-60
- Print publication:
- August 2019
-
- Article
-
- You have access
- Export citation
Finite Groups Whose Common-Divisor Graph is Regular
- Part of
-
- Journal:
- Proceedings of the Edinburgh Mathematical Society / Volume 61 / Issue 2 / May 2018
- Published online by Cambridge University Press:
- 15 February 2018, pp. 329-341
-
- Article
- Export citation
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS II
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 97 / Issue 2 / April 2018
- Published online by Cambridge University Press:
- 04 October 2017, pp. 215-217
- Print publication:
- April 2018
-
- Article
-
- You have access
- Export citation
ITÔ’S THEOREM AND MONOMIAL BRAUER CHARACTERS
- Part of
-
- Journal:
- Bulletin of the Australian Mathematical Society / Volume 96 / Issue 3 / December 2017
- Published online by Cambridge University Press:
- 08 June 2017, pp. 426-428
- Print publication:
- December 2017
-
- Article
-
- You have access
- Export citation
LANDAU’S THEOREM, FIELDS OF VALUES FOR CHARACTERS, AND SOLVABLE GROUPS
- Part of
-
- Journal:
- Journal of the Australian Mathematical Society / Volume 104 / Issue 1 / February 2018
- Published online by Cambridge University Press:
- 23 December 2016, pp. 37-43
- Print publication:
- February 2018
-
- Article
-
- You have access
- Export citation