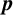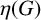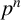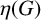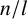1 Introduction
Unless otherwise stated, all groups in this paper are finite. Motivated by the research area of classifying spaces of families of subgroups of infinite groups, von Puttkamer asks [Reference von Puttkamer5, Question 5.0.9]: does the number of conjugacy classes of maximal cyclic subgroups of a finite p-group for a prime
![]() $p> 2$
grow with the order of the group? Clearly, the question is considering noncyclic groups. More precisely, one can ask whether the number of conjugacy classes of maximal cyclic subgroups of a noncyclic p-group of order
$p> 2$
grow with the order of the group? Clearly, the question is considering noncyclic groups. More precisely, one can ask whether the number of conjugacy classes of maximal cyclic subgroups of a noncyclic p-group of order
![]() $p^n$
is at least n when p is an odd prime. This work was initiated by X. Wu asking the second author this question in a private communication.
$p^n$
is at least n when p is an odd prime. This work was initiated by X. Wu asking the second author this question in a private communication.
The question can be phrased in terms of the size of a particular type of covering of a group. Recall, a covering of a group G is a set of proper subgroups
![]() $\{ H_i\}$
, called components, such that
$\{ H_i\}$
, called components, such that
![]() $G \subseteq \bigcup _i H_i$
. A covering is called irredundant if removing any component means the set is no longer a covering. A normal covering of G is a covering that is invariant under conjugation by G. Note that the components of a normal covering are not normal, but the components form orbits under conjugacy. Often, one takes only one representative of each conjugacy class of components. Our question above considers normal coverings where all the components of the cover are cyclic. It is not difficult to see that the set of maximal cyclic subgroups is the only irredundant covering by cyclic subgroups.
$G \subseteq \bigcup _i H_i$
. A covering is called irredundant if removing any component means the set is no longer a covering. A normal covering of G is a covering that is invariant under conjugation by G. Note that the components of a normal covering are not normal, but the components form orbits under conjugacy. Often, one takes only one representative of each conjugacy class of components. Our question above considers normal coverings where all the components of the cover are cyclic. It is not difficult to see that the set of maximal cyclic subgroups is the only irredundant covering by cyclic subgroups.
With this in mind, we introduce the following definition. Let G be a finite group. Denote the number of conjugacy classes of maximal cyclic subgroups of G by
![]() $\eta (G)$
. We note that the questions of von Puttkamer and Wu have negative answers. In [Reference Bianchi, Camina, Lewis and Pacifici1], the second and third authors along with Yiftach Barnea and Mikhail Ershov find for every prime
$\eta (G)$
. We note that the questions of von Puttkamer and Wu have negative answers. In [Reference Bianchi, Camina, Lewis and Pacifici1], the second and third authors along with Yiftach Barnea and Mikhail Ershov find for every prime
![]() $p> 3$
and every integer
$p> 3$
and every integer
![]() $n \ge 3$
, groups of order
$n \ge 3$
, groups of order
![]() $p^n$
that all have
$p^n$
that all have
![]() $\eta = p+2$
. For
$\eta = p+2$
. For
![]() $p = 2$
, we also find that
$p = 2$
, we also find that
![]() $\eta (G) = 3$
when G is a dihedral
$\eta (G) = 3$
when G is a dihedral
![]() $2$
-group, a generalised quaternion
$2$
-group, a generalised quaternion
![]() $2$
-group or a semi-dihedral
$2$
-group or a semi-dihedral
![]() $2$
-group. For
$2$
-group. For
![]() $p = 3$
, there is an infinite family of
$p = 3$
, there is an infinite family of
![]() $3$
-groups with
$3$
-groups with
![]() $\eta = 9$
(see [Reference Bianchi, Camina, Lewis and Pacifici1, Theorem 7.12]).
$\eta = 9$
(see [Reference Bianchi, Camina, Lewis and Pacifici1, Theorem 7.12]).
However, we believe it is extremely rare for this to occur. In particular, we prove that if we fix the nilpotence class of a p-group G, then
![]() $\eta (G)$
will grow proportionally to
$\eta (G)$
will grow proportionally to
![]() $\log _p (|G|)$
. The theorem we prove is the following.
$\log _p (|G|)$
. The theorem we prove is the following.
Theorem 1.1. Let G be a noncyclic p-group of nilpotence class
![]() $l \ge 1$
and order
$l \ge 1$
and order
![]() $p^n$
. Then
$p^n$
. Then
![]() $\eta (G) \ge (p-1)(n/l - 2) + p + 1$
.
$\eta (G) \ge (p-1)(n/l - 2) + p + 1$
.
2 Abelian groups
As noted in the introduction, when considering abelian groups calculating
![]() $\eta (G)$
is the same as calculating the maximum number of subgroups in an irredundant cyclic covering of G. In [Reference Rogério4, Proposition 6(ii)], the author gives a formula, which involves the Euler totient function, for calculating this number.
$\eta (G)$
is the same as calculating the maximum number of subgroups in an irredundant cyclic covering of G. In [Reference Rogério4, Proposition 6(ii)], the author gives a formula, which involves the Euler totient function, for calculating this number.
We take a slightly different approach; so we are including our results. We will show for abelian p-groups that a function in
![]() $\eta (G)$
gives a lower bound for
$\eta (G)$
gives a lower bound for
![]() $|G|$
. We begin by computing
$|G|$
. We begin by computing
![]() $\eta (G)$
when G is the direct product of two cyclic p-groups.
$\eta (G)$
when G is the direct product of two cyclic p-groups.
We consider the set
![]() $G^{\{p\}} = \{ g^p \mid g \in G \}$
. For an element
$G^{\{p\}} = \{ g^p \mid g \in G \}$
. For an element
![]() $g \in G$
, it is not difficult to see that
$g \in G$
, it is not difficult to see that
![]() $\langle g \rangle $
is a maximal cyclic subgroup of G if and only if
$\langle g \rangle $
is a maximal cyclic subgroup of G if and only if
![]() $g \in G \setminus G^{\{p\}}$
.
$g \in G \setminus G^{\{p\}}$
.
Lemma 2.1. Suppose
![]() $G \cong C_{p^a} \times C_{p^b}$
with
$G \cong C_{p^a} \times C_{p^b}$
with
![]() $a \geq b$
. Then
$a \geq b$
. Then
Proof. Let
![]() $G = \langle x \rangle \times \langle y \rangle $
with x of order
$G = \langle x \rangle \times \langle y \rangle $
with x of order
![]() $p^a$
and y of order
$p^a$
and y of order
![]() $p^b$
. Let C be a cyclic subgroup of G. Either C is a subgroup of
$p^b$
. Let C be a cyclic subgroup of G. Either C is a subgroup of
![]() $\langle (1,y) \rangle $
or there exist integers n and c so that C is generated by
$\langle (1,y) \rangle $
or there exist integers n and c so that C is generated by
![]() $(x^{p^n},y^c)$
for
$(x^{p^n},y^c)$
for
![]() $0 \leq n < a$
and
$0 \leq n < a$
and
![]() $0 \leq c < p^b$
. We claim that C is maximal exactly when
$0 \leq c < p^b$
. We claim that C is maximal exactly when
![]() $n = 0$
, or c is relatively prime to p or
$n = 0$
, or c is relatively prime to p or
![]() $C = \langle (1,y) \rangle $
. To see this, observe that in each of these cases, a generator of C does not lie in
$C = \langle (1,y) \rangle $
. To see this, observe that in each of these cases, a generator of C does not lie in
![]() $G^{\{p\}}$
, so C is maximal. Furthermore, we claim that the generator for a maximal cyclic subgroup is unique if we make the additional restriction that
$G^{\{p\}}$
, so C is maximal. Furthermore, we claim that the generator for a maximal cyclic subgroup is unique if we make the additional restriction that
![]() $0 \leq c < \min (p^b, p^{a-n})$
. First note for an integer l that
$0 \leq c < \min (p^b, p^{a-n})$
. First note for an integer l that
![]() $(x^{p^n}, y^c)^{1 + lp^{a-n}} = (x^{p^n}, y^{c + clp^{a-n}})$
. Since c is coprime to p, as l runs through the integers modulo
$(x^{p^n}, y^c)^{1 + lp^{a-n}} = (x^{p^n}, y^{c + clp^{a-n}})$
. Since c is coprime to p, as l runs through the integers modulo
![]() $p^b$
, then also
$p^b$
, then also
![]() $cl$
will run through all of
$cl$
will run through all of
![]() ${\mathbb Z}_{p^b}$
. So we are getting as the exponents for y, all elements in the coset
${\mathbb Z}_{p^b}$
. So we are getting as the exponents for y, all elements in the coset
![]() $c + p^{a-n} {\mathbb Z}_{p^b}$
in
$c + p^{a-n} {\mathbb Z}_{p^b}$
in
![]() ${\mathbb Z}_{p^b}$
. It is not difficult to see that
${\mathbb Z}_{p^b}$
. It is not difficult to see that
![]() $\{0,1,\ldots ,p^{a-n} -1\}$
is a transversal for
$\{0,1,\ldots ,p^{a-n} -1\}$
is a transversal for
![]() $p^{a-n}{\mathbb Z}_{p^b}$
in
$p^{a-n}{\mathbb Z}_{p^b}$
in
![]() ${\mathbb Z}_{p^b}$
. Hence, there exists an integer
${\mathbb Z}_{p^b}$
. Hence, there exists an integer
![]() $c'$
with
$c'$
with
![]() $0 \le c' \le p^{a-n}-1$
so that
$0 \le c' \le p^{a-n}-1$
so that
![]() $c' + p^{a-n}{\mathbb Z}_{p^b} = c + p^{a-n}{\mathbb Z}_{p^b}$
. It follows that
$c' + p^{a-n}{\mathbb Z}_{p^b} = c + p^{a-n}{\mathbb Z}_{p^b}$
. It follows that
![]() $(x^{p^n},y^{c'})$
will lie in
$(x^{p^n},y^{c'})$
will lie in
![]() $\langle (x^{p^n},y^c) \rangle $
and since it has the same order, it will be a generator.
$\langle (x^{p^n},y^c) \rangle $
and since it has the same order, it will be a generator.
So, we claim the following are distinct maximal cyclic subgroups of G:
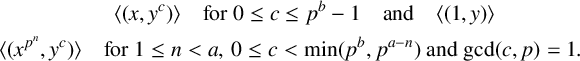 $$ \begin{align*} &\hspace{3pt}\quad\qquad\qquad\langle (x, y^c) \rangle\quad \mbox{for } 0 \leq c \leq p^{b}-1\quad \mbox{and}\quad \langle (1, y) \rangle \\ &\langle (x^{p^n}, y^c) \rangle\quad\mbox{for } 1 \leq n < a,\, 0 \leq c < \min(p^b, p^{a-n})\mbox{ and } {\textrm{gcd}}(c,p) =1. \end{align*} $$
$$ \begin{align*} &\hspace{3pt}\quad\qquad\qquad\langle (x, y^c) \rangle\quad \mbox{for } 0 \leq c \leq p^{b}-1\quad \mbox{and}\quad \langle (1, y) \rangle \\ &\langle (x^{p^n}, y^c) \rangle\quad\mbox{for } 1 \leq n < a,\, 0 \leq c < \min(p^b, p^{a-n})\mbox{ and } {\textrm{gcd}}(c,p) =1. \end{align*} $$
To count the number of subgroups of the form
![]() $\langle (x^{p^n}, y^c) \rangle $
, we consider two cases: when
$\langle (x^{p^n}, y^c) \rangle $
, we consider two cases: when
![]() $1 \leq n \leq a-b$
and when
$1 \leq n \leq a-b$
and when
![]() $a-b+1 \leq n < a$
. For
$a-b+1 \leq n < a$
. For
![]() $1 \leq n \leq a-b$
, we have
$1 \leq n \leq a-b$
, we have
![]() $\phi (p^b) = p^{b-1}(p-1)$
such subgroups, where
$\phi (p^b) = p^{b-1}(p-1)$
such subgroups, where
![]() $\phi $
is the Euler totient function. For
$\phi $
is the Euler totient function. For
![]() $a-b+1 \leq n \leq a-1$
, we have
$a-b+1 \leq n \leq a-1$
, we have
![]() $\phi (p^{a-n})$
maximal cyclic subgroups of the form
$\phi (p^{a-n})$
maximal cyclic subgroups of the form
![]() $ \langle x^{p^n},y^c \rangle $
, where p does not divide c and
$ \langle x^{p^n},y^c \rangle $
, where p does not divide c and
![]() $1 \leq c \leq p^{a-n}$
. With this range on b, we obtain
$1 \leq c \leq p^{a-n}$
. With this range on b, we obtain
![]() $1 \leq a-n \leq b-1$
. Observe that
$1 \leq a-n \leq b-1$
. Observe that
![]() $\phi (p^{a-n}) = p^{a-n-1} (p-1)$
. We can view this as
$\phi (p^{a-n}) = p^{a-n-1} (p-1)$
. We can view this as
![]() $p^{i-1} (p-1)$
for i running from 1 to
$p^{i-1} (p-1)$
for i running from 1 to
![]() $b-1$
or
$b-1$
or
![]() $p^i (p-1)$
for i running from 0 to
$p^i (p-1)$
for i running from 0 to
![]() $b-2$
. So, in total, we have
$b-2$
. So, in total, we have
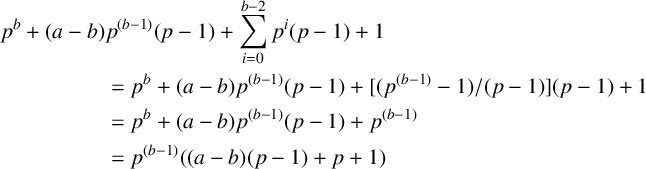 $$ \begin{align*} p^b + (a-b)&p^{(b-1)} (p-1) + \sum_{i=0}^{b-2} p^i(p-1) + 1 \\ & = p^b + (a-b) p^{(b-1)} (p-1) + [(p^{(b-1)} - 1)/(p-1)] (p-1) + 1 \\ & = p^b + (a-b) p^{(b-1)} (p-1) + p^{(b-1)} \\ & = p^{(b-1)} ((a - b)(p-1) + p + 1) \end{align*} $$
$$ \begin{align*} p^b + (a-b)&p^{(b-1)} (p-1) + \sum_{i=0}^{b-2} p^i(p-1) + 1 \\ & = p^b + (a-b) p^{(b-1)} (p-1) + [(p^{(b-1)} - 1)/(p-1)] (p-1) + 1 \\ & = p^b + (a-b) p^{(b-1)} (p-1) + p^{(b-1)} \\ & = p^{(b-1)} ((a - b)(p-1) + p + 1) \end{align*} $$
maximal cyclic subgroups, as desired. A simple inductive argument shows that
![]() $p^{b-1}((a-b)(p-1) + p + 1) \geq a+b$
.
$p^{b-1}((a-b)(p-1) + p + 1) \geq a+b$
.
It is useful to have a function which encodes this value. Let p be a prime, and let a and b be positive integers. We take
![]() $k = {\max } (a,b)$
and
$k = {\max } (a,b)$
and
![]() $l = {\min } (a,b)$
. We set
$l = {\min } (a,b)$
. We set
![]() $g_p (a,b) = p^{l-1}((k-l) (p-1) + p + 1)$
, so
$g_p (a,b) = p^{l-1}((k-l) (p-1) + p + 1)$
, so
![]() $g_p (a,b) = \eta (G)$
when
$g_p (a,b) = \eta (G)$
when
![]() $G = C_{p^a} \times C_{p^b}$
. In the next lemma, we obtain the lower bound that we need to prove the general lower bound for abelian groups.
$G = C_{p^a} \times C_{p^b}$
. In the next lemma, we obtain the lower bound that we need to prove the general lower bound for abelian groups.
Lemma 2.2. Let a and b be positive integers and p a prime. Then
Proof. Without loss of generality, we may assume
![]() $a \ge b$
. Set
$a \ge b$
. Set
![]() $n = a+b$
, so that
$n = a+b$
, so that
![]() $a = n - b$
. We work to show
$a = n - b$
. We work to show
![]() $g_p (a,b) \ge (p-1)(n-2) + p + 1 \geq n + 1$
. We observe that
$g_p (a,b) \ge (p-1)(n-2) + p + 1 \geq n + 1$
. We observe that
![]() $1 \le b \le n/2$
. We see that
$1 \le b \le n/2$
. We see that
![]() $g_p (n-b,b) = p^{b-1} ((n-2b)(p-1) + p+1)$
. We can view n as fixed, and this becomes a function in one variable:
$g_p (n-b,b) = p^{b-1} ((n-2b)(p-1) + p+1)$
. We can view n as fixed, and this becomes a function in one variable:
We want to find the minimal value for
![]() $f(x)$
on
$f(x)$
on
![]() $[1,n/2]$
. We use calculus to see that
$[1,n/2]$
. We use calculus to see that
Setting this equal to
![]() $0$
, we obtain the critical value of
$0$
, we obtain the critical value of
We claim that
![]() $(p+1)/(2(p-1)) - 1/(\ln p)$
is positive for all primes p. (This can be shown using calculus or graphing using a computer.) Hence, this critical point is not in our interval.
$(p+1)/(2(p-1)) - 1/(\ln p)$
is positive for all primes p. (This can be shown using calculus or graphing using a computer.) Hence, this critical point is not in our interval.
Now, we remark that
![]() $f(1) = ((n-2)(p-1)) + p +1 = p(n-1) -n +3$
and
$f(1) = ((n-2)(p-1)) + p +1 = p(n-1) -n +3$
and
![]() $f(n/2) = p^{n/2 - 1}(p+1)$
. Recall that Fermat’s theorem tells us that any local extreme values would occur when the derivative was zero. Since the derivative of this function is never zero on this interval, we know that our minimum is the smallest of these two values. Set
$f(n/2) = p^{n/2 - 1}(p+1)$
. Recall that Fermat’s theorem tells us that any local extreme values would occur when the derivative was zero. Since the derivative of this function is never zero on this interval, we know that our minimum is the smallest of these two values. Set
![]() $f_1(x) = ((x-2)(p-1)) + p + 1$
and
$f_1(x) = ((x-2)(p-1)) + p + 1$
and
![]() $f_{n/2}(x) = p^{x/2 -1}(p+1)$
for
$f_{n/2}(x) = p^{x/2 -1}(p+1)$
for
![]() $x \geq 2$
. Then
$x \geq 2$
. Then
![]() $f_1(2) = f_{n/2}(2)$
, but
$f_1(2) = f_{n/2}(2)$
, but
![]() $f^{\prime }_{n/2} (x)> f^{\prime }_{1} (x)$
; so
$f^{\prime }_{n/2} (x)> f^{\prime }_{1} (x)$
; so
![]() $f_{n/2}(x)> f_{1}(x)$
for
$f_{n/2}(x)> f_{1}(x)$
for
![]() $x> 2$
. Thus,
$x> 2$
. Thus,
![]() $g_p (n-b,b) \geq (p-1)(n-2) + p + 1$
. Finally, note that
$g_p (n-b,b) \geq (p-1)(n-2) + p + 1$
. Finally, note that
![]() $(p-1)(n-2) + p + 1 \geq n-2 + 3= n+1.$
$(p-1)(n-2) + p + 1 \geq n-2 + 3= n+1.$
We also need a refinement on the value of
![]() $\eta $
of a direct product of an abelian p-group with a cyclic p-group.
$\eta $
of a direct product of an abelian p-group with a cyclic p-group.
Lemma 2.3. Suppose
![]() $G \cong H \times C_{p^a}$
, where H is an abelian p-group. Then
$G \cong H \times C_{p^a}$
, where H is an abelian p-group. Then
Proof. We write
![]() $Y = \langle y \rangle \cong C_{p^a}$
, so that
$Y = \langle y \rangle \cong C_{p^a}$
, so that
![]() $G = H \times Y$
. Let
$G = H \times Y$
. Let
![]() $\{ h_i \}$
, for
$\{ h_i \}$
, for
![]() $1 \leq i \leq \eta (H)$
, be representatives of generators for the maximal cyclic subgroups of H. We now prove that
$1 \leq i \leq \eta (H)$
, be representatives of generators for the maximal cyclic subgroups of H. We now prove that
![]() $\langle (h_i, y^{p^c})\rangle $
, for
$\langle (h_i, y^{p^c})\rangle $
, for
![]() $0 \le c \le a$
and
$0 \le c \le a$
and
![]() $1 \leq i \leq \eta (H)$
, along with
$1 \leq i \leq \eta (H)$
, along with
![]() $\langle (1,y)\rangle $
are distinct maximal cyclic subgroups of G. This gives the required count for the lower bound.
$\langle (1,y)\rangle $
are distinct maximal cyclic subgroups of G. This gives the required count for the lower bound.
First note that
![]() $h_i \in H \setminus H^{\{p\} }$
, since
$h_i \in H \setminus H^{\{p\} }$
, since
![]() $\langle h_i \rangle $
is maximal in H, and thus,
$\langle h_i \rangle $
is maximal in H, and thus,
![]() $(h_i, 1)$
,
$(h_i, 1)$
,
![]() $(h_i, y^{p^c})$
and
$(h_i, y^{p^c})$
and
![]() $(1, y)$
all lie in
$(1, y)$
all lie in
![]() $G \setminus G^{\{p\} }$
for
$G \setminus G^{\{p\} }$
for
![]() $c \in \{ 0, \ldots , a \}$
. (It is not difficult to see that
$c \in \{ 0, \ldots , a \}$
. (It is not difficult to see that
![]() $G^{\{p\} } = \{ (\alpha ,\beta ) \mid \alpha \in H^{\{ p\} }, \beta \in \langle y^p \rangle \}$
.) Thus, each of these elements generate a maximal cyclic subgroup of G. We need to show that they generate different cyclic subgroups of G. Suppose
$G^{\{p\} } = \{ (\alpha ,\beta ) \mid \alpha \in H^{\{ p\} }, \beta \in \langle y^p \rangle \}$
.) Thus, each of these elements generate a maximal cyclic subgroup of G. We need to show that they generate different cyclic subgroups of G. Suppose
![]() $\langle (h_i, y^{p^c})\rangle = \langle (h_j, y^{p^d})\rangle $
for
$\langle (h_i, y^{p^c})\rangle = \langle (h_j, y^{p^d})\rangle $
for
![]() $0 \le c,d \le a$
. In both cases, by projecting into H, it is not difficult to see that
$0 \le c,d \le a$
. In both cases, by projecting into H, it is not difficult to see that
![]() $\langle h_i\rangle = \langle h_j\rangle $
, and thus,
$\langle h_i\rangle = \langle h_j\rangle $
, and thus,
![]() $i = j$
. We are left to consider
$i = j$
. We are left to consider
![]() $\langle (h_i, y^{p^c})\rangle = \langle (h_i, y^{p^d})\rangle $
. Projecting into Y, this forces
$\langle (h_i, y^{p^c})\rangle = \langle (h_i, y^{p^d})\rangle $
. Projecting into Y, this forces
![]() $\langle y^{p^c}\rangle = \langle y^{p^d} \rangle $
, and thus,
$\langle y^{p^c}\rangle = \langle y^{p^d} \rangle $
, and thus,
![]() $c=d$
as required.
$c=d$
as required.
We now obtain our lower bound on
![]() $\log _p (|G|)$
when G is an abelian p-group in terms of
$\log _p (|G|)$
when G is an abelian p-group in terms of
![]() $\eta (G)$
.
$\eta (G)$
.
Theorem 2.4. Let G be an abelian, noncyclic group of order
![]() $p^n$
. Then
$p^n$
. Then
Proof. We work by induction on
![]() $|G|$
. Suppose first that
$|G|$
. Suppose first that
![]() $G = C_{p^a} \times C_{p^b}$
for positive integers a and b. By Lemma 2.1, we have
$G = C_{p^a} \times C_{p^b}$
for positive integers a and b. By Lemma 2.1, we have
![]() $\eta (G) = g_p (a,b)$
and applying Lemma 2.2,
$\eta (G) = g_p (a,b)$
and applying Lemma 2.2,
![]() $g_p (a,b) \ge (p-1)(a+b-2) + p + 1 \ge a+b + 1$
.
$g_p (a,b) \ge (p-1)(a+b-2) + p + 1 \ge a+b + 1$
.
Now suppose H is not cyclic and
![]() $|H| = p^h$
and
$|H| = p^h$
and
![]() $G = H \times C_{p^a}.$
By induction,
$G = H \times C_{p^a}.$
By induction,
![]() $\eta (H) \ge (p-1)(h-2) + p + 1$
. By Lemma 2.3,
$\eta (H) \ge (p-1)(h-2) + p + 1$
. By Lemma 2.3,
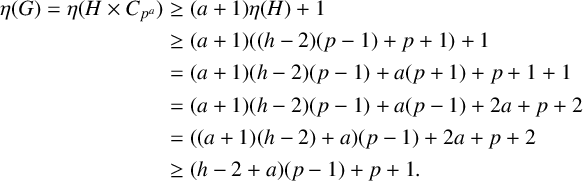 $$ \begin{align*} \eta (G) = \eta (H \times C_{p^a}) & \ge (a + 1) \eta (H)+ 1 \\ & \ge (a + 1)((h-2)(p-1) + p + 1) + 1 \\ & = (a+1)(h-2)(p-1) + a (p+1) + p + 1 + 1 \\ & = (a+1)(h-2)(p-1) + a (p-1) + 2a + p + 2 \\ & = ((a+1)(h-2) + a)(p-1) + 2a + p + 2 \\ & \ge (h - 2 + a)(p-1) + p + 1. \end{align*} $$
$$ \begin{align*} \eta (G) = \eta (H \times C_{p^a}) & \ge (a + 1) \eta (H)+ 1 \\ & \ge (a + 1)((h-2)(p-1) + p + 1) + 1 \\ & = (a+1)(h-2)(p-1) + a (p+1) + p + 1 + 1 \\ & = (a+1)(h-2)(p-1) + a (p-1) + 2a + p + 2 \\ & = ((a+1)(h-2) + a)(p-1) + 2a + p + 2 \\ & \ge (h - 2 + a)(p-1) + p + 1. \end{align*} $$
Since
![]() $n = h + a$
, this gives the result.
$n = h + a$
, this gives the result.
Finally, note that
![]() $(p-1)(n-2) + p + 1 \geq n-2 + 3= n+1.$
$(p-1)(n-2) + p + 1 \geq n-2 + 3= n+1.$
When p is odd, we can improve the inequality in Theorem 2.4.
Corollary 2.5. If p is odd and G is a noncyclic, abelian group of order
![]() $p^n$
, then
$p^n$
, then
Proof. We apply the result from Theorem 2.4:
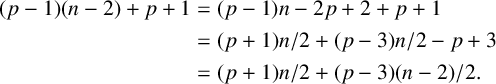 $$ \begin{align*} (p-1)(n-2) + p + 1 & = (p-1)n -2p + 2 + p + 1 \\ & = (p+1)n/2 + (p-3)n/2 - p + 3\\ & = (p+1)n/2 + (p-3)(n-2)/2. \end{align*} $$
$$ \begin{align*} (p-1)(n-2) + p + 1 & = (p-1)n -2p + 2 + p + 1 \\ & = (p+1)n/2 + (p-3)n/2 - p + 3\\ & = (p+1)n/2 + (p-3)(n-2)/2. \end{align*} $$
Since
![]() $p \ge 3$
and
$p \ge 3$
and
![]() $n \ge 2$
, this is at least
$n \ge 2$
, this is at least
![]() $(p+1)n/2$
.
$(p+1)n/2$
.
3
 $\boldsymbol {\eta }$
and nilpotence class
$\boldsymbol {\eta }$
and nilpotence class
We now show that if we fix the nilpotence class of a p-group G, then a function of
![]() $\eta (G)$
gives a lower bound for
$\eta (G)$
gives a lower bound for
![]() $|G|$
. We will see that this can be viewed as a generalisation of Theorem 2.4 for abelian groups. We define the terms of the lower central series of G inductively as follows:
$|G|$
. We will see that this can be viewed as a generalisation of Theorem 2.4 for abelian groups. We define the terms of the lower central series of G inductively as follows:
![]() $G^1 = G$
and
$G^1 = G$
and
![]() $G^{i+1} = [G^{i},G]$
for
$G^{i+1} = [G^{i},G]$
for
![]() $i \ge 1$
. Observe that G is nilpotent of nilpotence class l if
$i \ge 1$
. Observe that G is nilpotent of nilpotence class l if
![]() $G^{l+1} = 1$
and
$G^{l+1} = 1$
and
![]() $G^l> 1$
.
$G^l> 1$
.
We first prove a lemma regarding the order of elements of
![]() $G^l$
when G has nilpotence class l. Taking
$G^l$
when G has nilpotence class l. Taking
![]() $|G| = p^n$
, note that
$|G| = p^n$
, note that
![]() $n \ge l+1$
, so
$n \ge l+1$
, so
![]() $\lfloor n/(l+1) \rfloor \ge 1$
. It has been suggested that this next lemma is related to [Reference Easterfield3].
$\lfloor n/(l+1) \rfloor \ge 1$
. It has been suggested that this next lemma is related to [Reference Easterfield3].
Lemma 3.1. Let G be a p-group of nilpotence class
![]() $l \ge 2$
and order
$l \ge 2$
and order
![]() $p^n$
. Then
$p^n$
. Then
![]() $G^l$
has exponent dividing
$G^l$
has exponent dividing
![]() $p^{\lfloor n/(l+1) \rfloor }$
.
$p^{\lfloor n/(l+1) \rfloor }$
.
Proof. We work by induction on l. We begin with the case
![]() $l = 2$
. If
$l = 2$
. If
![]() $|G^2| \le p^{n/3}$
, then we have the result. Thus, we may assume that
$|G^2| \le p^{n/3}$
, then we have the result. Thus, we may assume that
![]() $|G^2|> p^{ n/3}$
and so,
$|G^2|> p^{ n/3}$
and so,
![]() $|G/G^2| < p^{2n/3}$
. We can find
$|G/G^2| < p^{2n/3}$
. We can find
![]() $a_1, \ldots , a_k \in G$
so that
$a_1, \ldots , a_k \in G$
so that
![]() $G/G^2 = \langle a_1 G^2 \rangle \times \langle a_2 G^2 \rangle \times \cdots \times \langle a_k G^2 \rangle $
. We know that
$G/G^2 = \langle a_1 G^2 \rangle \times \langle a_2 G^2 \rangle \times \cdots \times \langle a_k G^2 \rangle $
. We know that
![]() $G^2$
is central and so it is abelian. Also, it is generated by
$G^2$
is central and so it is abelian. Also, it is generated by
![]() $\{ [a_i,a_j] \mid 1 \le i < j \le k \}$
. Since G is a p-group, it suffices to show that
$\{ [a_i,a_j] \mid 1 \le i < j \le k \}$
. Since G is a p-group, it suffices to show that
![]() $o([a_i,a_j])$
is less than or equal to
$o([a_i,a_j])$
is less than or equal to
![]() $p^{n/3}$
for all
$p^{n/3}$
for all
![]() $1 \le i < j \le k$
. Observe that
$1 \le i < j \le k$
. Observe that
![]() $o(a_iG^2)o(a_jG^2)$
divides
$o(a_iG^2)o(a_jG^2)$
divides
![]() $|G/G^2| < p^{2n/3}$
and so, without loss of generality,
$|G/G^2| < p^{2n/3}$
and so, without loss of generality,
![]() $o(a_iG^2)$
is less than or equal to
$o(a_iG^2)$
is less than or equal to
![]() $p^{n/3}$
. Now,
$p^{n/3}$
. Now,
![]() $[a_i,a_j]^{\lfloor n/3 \rfloor } = [a_i^{\lfloor n/3\rfloor },a_j] = 1$
. This completes the proof when
$[a_i,a_j]^{\lfloor n/3 \rfloor } = [a_i^{\lfloor n/3\rfloor },a_j] = 1$
. This completes the proof when
![]() $l = 2$
.
$l = 2$
.
We now assume that
![]() $l \ge 2$
. If
$l \ge 2$
. If
![]() $|G^l| \le p^{n/(l+1)}$
, then the result holds. Thus, we may assume that
$|G^l| \le p^{n/(l+1)}$
, then the result holds. Thus, we may assume that
![]() $|G^l|> p^{n/(l+1)}$
, and so,
$|G^l|> p^{n/(l+1)}$
, and so,
![]() $|G/G^l| < p^{nl/(l+1)}$
. We see that
$|G/G^l| < p^{nl/(l+1)}$
. We see that
![]() $G^l$
is generated by the set
$G^l$
is generated by the set
![]() $\{[a,b] \mid a \in G^{l-1}, b \in G \}$
. As above, since
$\{[a,b] \mid a \in G^{l-1}, b \in G \}$
. As above, since
![]() $G^l$
is central (thus abelian) and a p-group, it suffices to show that
$G^l$
is central (thus abelian) and a p-group, it suffices to show that
![]() $o([a,b]) \le p^{n/{(l+1)}}$
when
$o([a,b]) \le p^{n/{(l+1)}}$
when
![]() $a \in G^{l-1}$
and
$a \in G^{l-1}$
and
![]() $b \in G$
. By induction, we know since
$b \in G$
. By induction, we know since
![]() $G/G^l$
has nilpotence class
$G/G^l$
has nilpotence class
![]() $l-1$
that
$l-1$
that
![]() $o(a G^l)$
is less than or equal to
$o(a G^l)$
is less than or equal to
![]() $p^{(nl/(l+1))/l} = p^{n/(l+1)}$
. We then have
$p^{(nl/(l+1))/l} = p^{n/(l+1)}$
. We then have
![]() $[a,b]^{\lfloor n/(l+1) \rfloor } = [a^{\lfloor n/(l+1) \rfloor },b] = 1$
. This proves the desired result.
$[a,b]^{\lfloor n/(l+1) \rfloor } = [a^{\lfloor n/(l+1) \rfloor },b] = 1$
. This proves the desired result.
We now have what we need to prove the theorem. Notice that when
![]() $l = 1$
, G is abelian and the inequality is the inequality that was proved in Theorem 2.4. Thus, we can use the abelian case as the base case for our induction. We need two results that we have proved in [Reference Barnea, Camina, Ershov and Lewis2]: (1) If N is a normal subgroup of G, then
$l = 1$
, G is abelian and the inequality is the inequality that was proved in Theorem 2.4. Thus, we can use the abelian case as the base case for our induction. We need two results that we have proved in [Reference Barnea, Camina, Ershov and Lewis2]: (1) If N is a normal subgroup of G, then
![]() $\eta (G) \ge \eta (G/N)$
; (2) If G is a group, then
$\eta (G) \ge \eta (G/N)$
; (2) If G is a group, then
![]() $\eta (G) \ge \eta (Z(G))$
.
$\eta (G) \ge \eta (Z(G))$
.
Proof of Theorem 1.1
We work by induction on l. If
![]() $l = 1$
, then this is Theorem 2.4.
$l = 1$
, then this is Theorem 2.4.
We now suppose that
![]() $l \ge 2$
. Note that
$l \ge 2$
. Note that
![]() $G/G' = G/G^2$
is not cyclic, so the induction hypothesis is valid even if
$G/G' = G/G^2$
is not cyclic, so the induction hypothesis is valid even if
![]() $l =2$
. If
$l =2$
. If
![]() $|G/G^l| \ge p^{n(l-1)/l}$
, then by the induction hypothesis,
$|G/G^l| \ge p^{n(l-1)/l}$
, then by the induction hypothesis,
As we noted before the start of the proof,
![]() $\eta (G) \ge \eta (G/G^l)$
, and so we have the conclusion in this case.
$\eta (G) \ge \eta (G/G^l)$
, and so we have the conclusion in this case.
Thus, we may assume that
![]() $|G/G^l| < p^{n(l-1)/l}$
and so
$|G/G^l| < p^{n(l-1)/l}$
and so
![]() $|G^l|> p^{(n/l)} > p^{n/(l+1)}$
. By Lemma 3.1, this implies that
$|G^l|> p^{(n/l)} > p^{n/(l+1)}$
. By Lemma 3.1, this implies that
![]() $G^l$
is not cyclic. It follows that
$G^l$
is not cyclic. It follows that
![]() $|Z(G)|> p^{n/l}$
and
$|Z(G)|> p^{n/l}$
and
![]() $Z(G)$
is not cyclic. By Theorem 2.4,
$Z(G)$
is not cyclic. By Theorem 2.4,
![]() $\eta (Z(G)) \ge (p-1)(n/l - 2) + p + 1$
, and as we noted before the start of the proof, we have
$\eta (Z(G)) \ge (p-1)(n/l - 2) + p + 1$
, and as we noted before the start of the proof, we have
![]() $\eta (G) \ge \eta (Z(G))$
. This yields the result when
$\eta (G) \ge \eta (Z(G))$
. This yields the result when
![]() $n = l$
and proves the theorem.
$n = l$
and proves the theorem.
Rewriting the inequality in Theorem 1.1, we obtain
So Theorem 1.1 can be viewed as saying that that the size of G is bounded in terms of a function of
![]() $\eta (G)$
and the nilpotence class of G. That is, if the order of G is growing, then either
$\eta (G)$
and the nilpotence class of G. That is, if the order of G is growing, then either
![]() $\eta $
or l (or both) must be growing. If one fixes
$\eta $
or l (or both) must be growing. If one fixes
![]() $|G|$
, then the nilpotence class being small forces
$|G|$
, then the nilpotence class being small forces
![]() $\eta $
to be large and vice versa. In this way, it is like the uncertainty principle.
$\eta $
to be large and vice versa. In this way, it is like the uncertainty principle.
Acknowledgements
The authors would like to thank Emanuele Pacifici for a number of helpful conversations while working on this paper. We would like to thank Avinoam Mann for pointing out [Reference Easterfield3].