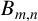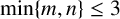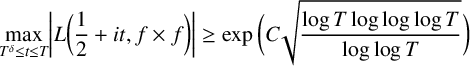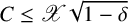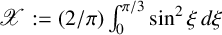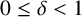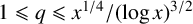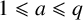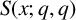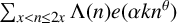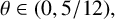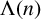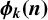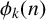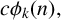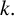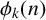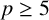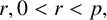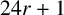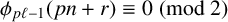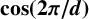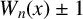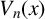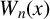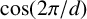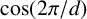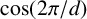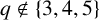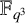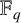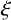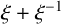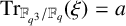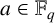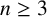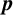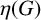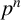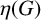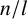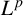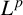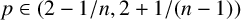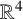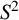Research Article
ON THE CAYLEYNESS OF PRAEGER–XU GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 11 May 2022, pp. 353-356
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A NOTE ON THE SINGULARITY OF ORIENTED GRAPHS
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2022, pp. 357-362
-
- Article
- Export citation
BINARY SIGNED-DIGIT REPRESENTATIONS IN PAPERFOLDING
- Part of:
-
- Published online by Cambridge University Press:
- 10 June 2022, pp. 363-375
-
- Article
- Export citation
ON LINEARISED POLYNOMIALS, SIDON ARRAYS AND FAST CONSTRUCTION OF SIDON SETS
- Part of:
-
- Published online by Cambridge University Press:
- 30 August 2022, pp. 376-384
-
- Article
- Export citation
ALTERNATING CIRCULAR SUMS OF BINOMIAL COEFFICIENTS
- Part of:
-
- Published online by Cambridge University Press:
- 13 April 2022, pp. 385-395
-
- Article
- Export citation
ON THE INHOMOGENEOUS VINOGRADOV SYSTEM
- Part of:
-
- Published online by Cambridge University Press:
- 19 April 2022, pp. 396-403
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
SOLVABILITY OF A SYSTEM OF POLYNOMIAL EQUATIONS MODULO PRIMES
- Part of:
-
- Published online by Cambridge University Press:
- 23 March 2022, pp. 404-407
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
EXTREME VALUES OF THE RANKIN–SELBERG
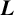 $\boldsymbol {L}$
-FUNCTIONS
$\boldsymbol {L}$
-FUNCTIONS
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2022, pp. 408-418
-
- Article
- Export citation
DISTRIBUTION OF ELEMENTS OF A FLOOR FUNCTION SET IN ARITHMETICAL PROGRESSIONS
- Part of:
-
- Published online by Cambridge University Press:
- 01 March 2022, pp. 419-424
-
- Article
- Export citation
AVERAGES OF EXPONENTIAL TWISTS OF THE VON MANGOLDT FUNCTION
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2022, pp. 425-430
-
- Article
- Export citation
ON THE PARITY OF THE GENERALISED FROBENIUS PARTITION FUNCTIONS
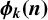 $\boldsymbol {\phi _k(n)}$
$\boldsymbol {\phi _k(n)}$
- Part of:
-
- Published online by Cambridge University Press:
- 15 June 2022, pp. 431-436
-
- Article
- Export citation
RECIPROCAL MONOGENIC QUINTINOMIALS OF DEGREE
 $\boldsymbol {2^n}$
$\boldsymbol {2^n}$
- Part of:
-
- Published online by Cambridge University Press:
- 04 March 2022, pp. 437-447
-
- Article
- Export citation
FACTORING VARIANTS OF CHEBYSHEV POLYNOMIALS WITH MINIMAL POLYNOMIALS OF
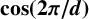 $\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
$\mathbf {cos}\boldsymbol {({2\pi }/{d})}$
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2022, pp. 448-457
-
- Article
- Export citation
PRIMITIVE ELEMENT PAIRS WITH A PRESCRIBED TRACE IN THE CUBIC EXTENSION OF A FINITE FIELD
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2022, pp. 458-462
-
- Article
- Export citation
CONJUGACY CLASSES OF MAXIMAL CYCLIC SUBGROUPS AND NILPOTENCE CLASS OF
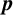 $\boldsymbol {p}$
-GROUPS
$\boldsymbol {p}$
-GROUPS
- Part of:
-
- Published online by Cambridge University Press:
- 21 March 2022, pp. 463-469
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
ON FRACTAL DIMENSIONS OF FRACTAL FUNCTIONS USING FUNCTION SPACES
- Part of:
-
- Published online by Cambridge University Press:
- 08 August 2022, pp. 470-480
-
- Article
- Export citation
 $\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
$\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2022, pp. 481-490
-
- Article
- Export citation
TRANSLATING SOLITONS FOR THE MEAN CURVATURE FLOW IN
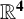 $\boldsymbol {{\mathbb {R}}^{4}}$
$\boldsymbol {{\mathbb {R}}^{4}}$
- Part of:
-
- Published online by Cambridge University Press:
- 25 April 2022, pp. 491-499
-
- Article
- Export citation
A CONTINUOUS HOMOMORPHISM OF A THIN SET ONTO A FAT SET
- Part of:
-
- Published online by Cambridge University Press:
- 01 April 2022, pp. 500-503
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
LIFTING HOMEOMORPHISMS AND FINITE ABELIAN BRANCHED COVERS OF THE 2-SPHERE
- Part of:
-
- Published online by Cambridge University Press:
- 02 June 2022, pp. 504-507
-
- Article
- Export citation