1 Scope of this note
The Praeger–Xu graphs, introduced by Praeger and Xu in [Reference Praeger and Xu2], have exponentially large groups of automorphisms, with respect to the number of vertices. This fact causes various complications with regard to many natural questions.
In their recent work [Reference Jajcay, Potočnik and Wilson1], Jajcay et al. gave a sufficient and necessary condition for a Praeger–Xu graph to be a Cayley graph. Explicitly, [Reference Jajcay, Potočnik and Wilson1, Theorem 1.1] states that, for any positive integer
![]() $n\geq 3$
,
$n\geq 3$
,
![]() $n\ne 4$
, and for any positive integer
$n\ne 4$
, and for any positive integer
![]() $k\leq n-1$
, the Praeger–Xu graph
$k\leq n-1$
, the Praeger–Xu graph
![]() $\textrm {PX}(n,k)$
is a Cayley graph if and only if one of the following holds:
$\textrm {PX}(n,k)$
is a Cayley graph if and only if one of the following holds:
-
(i) the polynomial
 $t^{n}+1$
has a divisor of degree
$t^{n}+1$
has a divisor of degree
 $n-k$
in
$n-k$
in
 $\mathbb {Z}_{2}[t]$
;
$\mathbb {Z}_{2}[t]$
; -
(ii) n is even, and there exist polynomials
 $f_{1},f_{2},g_{1},g_{2},u,v\in \mathbb {Z}_{2}[t]$
such that
$f_{1},f_{2},g_{1},g_{2},u,v\in \mathbb {Z}_{2}[t]$
such that
 $u,v$
are palindromic of degree
$u,v$
are palindromic of degree
 $n-k$
, and (1.1)
$n-k$
, and (1.1) $$ \begin{align} t^{n}+1 = f_{1}(t^{2})u(t) + tg_{1}(t^{2})v(t) = f_{2}(t^{2})v(t) + tg_{2}(t^{2})u(t). \end{align} $$
$$ \begin{align} t^{n}+1 = f_{1}(t^{2})u(t) + tg_{1}(t^{2})v(t) = f_{2}(t^{2})v(t) + tg_{2}(t^{2})u(t). \end{align} $$
Our aim here is to prove that (ii) implies (i), thus obtaining the following refinement. (It can be verified that
![]() $\textrm {PX}(4,1)$
,
$\textrm {PX}(4,1)$
,
![]() $\textrm {PX}(4,2)$
and
$\textrm {PX}(4,2)$
and
![]() $\textrm {PX}(4,3)$
are Cayley graphs.)
$\textrm {PX}(4,3)$
are Cayley graphs.)
Theorem 1.1. For any positive integer
![]() $n\geq 3$
and for any positive integer
$n\geq 3$
and for any positive integer
![]() $k\leq n-1$
, the Praeger–Xu graph
$k\leq n-1$
, the Praeger–Xu graph
![]() $\mathrm{PX}(n,k)$
is a Cayley graph if and only if the polynomial
$\mathrm{PX}(n,k)$
is a Cayley graph if and only if the polynomial
![]() $t^{n}+1$
has a divisor of degree
$t^{n}+1$
has a divisor of degree
![]() $n-k$
in
$n-k$
in
![]() $\mathbb {Z}_{2}[t]$
.
$\mathbb {Z}_{2}[t]$
.
Using the factorisation of
![]() $t^{n}+1$
in
$t^{n}+1$
in
![]() $\mathbb {Z}_{2}[t]$
, we give a purely arithmetic condition for the Cayleyness of
$\mathbb {Z}_{2}[t]$
, we give a purely arithmetic condition for the Cayleyness of
![]() $\textrm {PX}(n,k)$
. Let
$\textrm {PX}(n,k)$
. Let
![]() $\varphi $
be the Euler
$\varphi $
be the Euler
![]() $\varphi $
-function and, for every positive integer d, let
$\varphi $
-function and, for every positive integer d, let
be the multiplicative order of
![]() $2$
modulo d.
$2$
modulo d.
Corollary 1.2. Let a be a nonnegative integer, let b be an odd positive integer, let
![]() $n:=2^{a}b$
with
$n:=2^{a}b$
with
![]() $n\geq 3$
and let k be a positive integer with
$n\geq 3$
and let k be a positive integer with
![]() $k\leq n-1$
. The Praeger–Xu graph
$k\leq n-1$
. The Praeger–Xu graph
![]() $\mathrm{PX}(n,k)$
is a Cayley graph if and only if k can be written as
$\mathrm{PX}(n,k)$
is a Cayley graph if and only if k can be written as
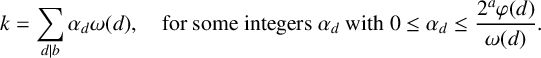 $$ \begin{align} k= \sum_{d\mid b} \alpha_{d} \omega(d),\quad \text{for some integers }\alpha_{d}\text{ with } 0\leq \alpha_{d} \leq \frac{2^{a}\varphi(d)}{\omega(d)}. \end{align} $$
$$ \begin{align} k= \sum_{d\mid b} \alpha_{d} \omega(d),\quad \text{for some integers }\alpha_{d}\text{ with } 0\leq \alpha_{d} \leq \frac{2^{a}\varphi(d)}{\omega(d)}. \end{align} $$
2 Proof of Theorem 1.1
Suppose (ii) holds. We aim to show that
![]() $t^{n}+1$
is divisible by a polynomial of degree
$t^{n}+1$
is divisible by a polynomial of degree
![]() $n-k$
in
$n-k$
in
![]() $\mathbb {Z}_{2}[t]$
, implying (i). Working in characteristic
$\mathbb {Z}_{2}[t]$
, implying (i). Working in characteristic
![]() $2$
, (1.1) can be written as
$2$
, (1.1) can be written as
in short,
If
![]() $g_{1}=0$
or if
$g_{1}=0$
or if
![]() $g_{2}=0$
, then the result follows from (2.1), and the fact that u and v have degree
$g_{2}=0$
, then the result follows from (2.1), and the fact that u and v have degree
![]() $n-k$
. Therefore, for the rest of the argument, we may suppose that
$n-k$
. Therefore, for the rest of the argument, we may suppose that
![]() $g_{1},g_{2}\ne 0$
. Moreover, observe that
$g_{1},g_{2}\ne 0$
. Moreover, observe that
![]() $f_{1},f_{2}\ne 0$
, because t does not divide
$f_{1},f_{2}\ne 0$
, because t does not divide
![]() $t^{n}+1$
.
$t^{n}+1$
.
We introduce four polynomials
![]() $u_{e},u_{o},v_{e},v_{o} \in \mathbb {Z}_{2}[t]$
such that
$u_{e},u_{o},v_{e},v_{o} \in \mathbb {Z}_{2}[t]$
such that
Substituting these expansions for u and v in (2.1),
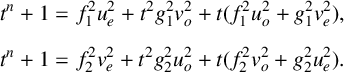 $$ \begin{align*} t^{n}+1&=f_{1}^{2}u_{e}^{2}+t^{2}g_{1}^{2}v_{o}^{2}+t(f_{1}^{2}u_{o}^{2}+g_{1}^{2}v_{e}^{2}),\\[5pt] t^{n}+1&=f_{2}^{2}v_{e}^{2}+t^{2}g_{2}^{2}u_{o}^{2}+t(f_{2}^{2}v_{o}^{2}+g_{2}^{2}u_{e}^{2}). \end{align*} $$
$$ \begin{align*} t^{n}+1&=f_{1}^{2}u_{e}^{2}+t^{2}g_{1}^{2}v_{o}^{2}+t(f_{1}^{2}u_{o}^{2}+g_{1}^{2}v_{e}^{2}),\\[5pt] t^{n}+1&=f_{2}^{2}v_{e}^{2}+t^{2}g_{2}^{2}u_{o}^{2}+t(f_{2}^{2}v_{o}^{2}+g_{2}^{2}u_{e}^{2}). \end{align*} $$
Recall that n is even. By splitting the equations into even and odd degree terms, we obtain
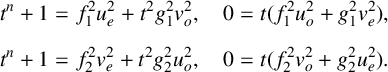 $$ \begin{align*} t^{n}+1&=f_{1}^{2}u_{e}^{2}+t^{2}g_{1}^{2}v_{o}^{2}, \quad 0=t(f_{1}^{2}u_{o}^{2}+g_{1}^{2}v_{e}^{2}),\\[5pt] t^{n}+1&=f_{2}^{2}v_{e}^{2}+t^{2}g_{2}^{2}u_{o}^{2}, \quad 0=t(f_{2}^{2}v_{o}^{2}+g_{2}^{2}u_{e}^{2}). \end{align*} $$
$$ \begin{align*} t^{n}+1&=f_{1}^{2}u_{e}^{2}+t^{2}g_{1}^{2}v_{o}^{2}, \quad 0=t(f_{1}^{2}u_{o}^{2}+g_{1}^{2}v_{e}^{2}),\\[5pt] t^{n}+1&=f_{2}^{2}v_{e}^{2}+t^{2}g_{2}^{2}u_{o}^{2}, \quad 0=t(f_{2}^{2}v_{o}^{2}+g_{2}^{2}u_{e}^{2}). \end{align*} $$
Set
![]() $m:=n/2$
. Since we are working in characteristic
$m:=n/2$
. Since we are working in characteristic
![]() $2$
,
$2$
,
Since u and v are palindromic by assumption, we get
![]() $1=u(0) =u_{e}(0)$
and
$1=u(0) =u_{e}(0)$
and
![]() ${1=v(0) =v_{e}(0)}$
. In particular, both
${1=v(0) =v_{e}(0)}$
. In particular, both
![]() $u_{e}$
and
$u_{e}$
and
![]() $v_{e}$
are not zero. From (2.2) and (2.3),
$v_{e}$
are not zero. From (2.2) and (2.3),
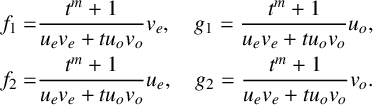 $$ \begin{align} f_{1}=&\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}v_{e}, \quad g_{1}=\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}u_{o},\nonumber\\ f_{2}=&\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}u_{e}, \quad g_{2}=\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}v_{o}. \end{align} $$
$$ \begin{align} f_{1}=&\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}v_{e}, \quad g_{1}=\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}u_{o},\nonumber\\ f_{2}=&\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}u_{e}, \quad g_{2}=\frac{t^{m}+1}{u_{e}v_{e}+tu_{o}v_{o}}v_{o}. \end{align} $$
Our candidate for the desired divisor of
![]() $t^{n} + 1$
is
$t^{n} + 1$
is
![]() $s:=u_{e}v_{e}+tu_{o}v_{o}$
. Let us show first that
$s:=u_{e}v_{e}+tu_{o}v_{o}$
. Let us show first that
![]() $\deg (s)=n - k$
. Since
$\deg (s)=n - k$
. Since
![]() $u_{e}v_{e}$
and
$u_{e}v_{e}$
and
![]() $u_{o}v_{o}$
have even degree, we deduce
$u_{o}v_{o}$
have even degree, we deduce
Recall
![]() $u=u_{e}^{2}+tu_{o}^{2}$
and
$u=u_{e}^{2}+tu_{o}^{2}$
and
![]() $v=v_{e}^{2}+tv_{o}^{2}$
. If
$v=v_{e}^{2}+tv_{o}^{2}$
. If
![]() $n-k$
is even, then
$n-k$
is even, then
However, if
![]() $n-k$
is odd, then
$n-k$
is odd, then
Therefore, in both cases,
![]() $\deg (s) = n-k$
.
$\deg (s) = n-k$
.
It remains to prove that s divides
![]() $t^{n}+1$
. Since
$t^{n}+1$
. Since
![]() $f_{1},g_{1},f_{2},g_{2}$
are polynomials, by (2.4), s divides
$f_{1},g_{1},f_{2},g_{2}$
are polynomials, by (2.4), s divides
Observe that
![]() $\gcd (v_{e},v_{o},u_{e},u_{o})$
divides
$\gcd (v_{e},v_{o},u_{e},u_{o})$
divides
![]() $f_{1}u_{e}+tg_{1}v_{o}$
, and hence, in view of the first equation in (2.2),
$f_{1}u_{e}+tg_{1}v_{o}$
, and hence, in view of the first equation in (2.2),
![]() $\gcd (v_{e},v_{o},u_{e},u_{o})$
divides
$\gcd (v_{e},v_{o},u_{e},u_{o})$
divides
![]() $t^{m}+1$
. Therefore, s divides
$t^{m}+1$
. Therefore, s divides
![]() ${(t^{m}+1)^{2}=t^{n}+1}$
.
${(t^{m}+1)^{2}=t^{n}+1}$
.
3 Proof of Corollary 1.2
By Theorem 1.1, deciding if a Praeger–Xu graph
![]() $\textrm {PX}(n,k)$
is a Cayley graph is tantamount to deciding if
$\textrm {PX}(n,k)$
is a Cayley graph is tantamount to deciding if
![]() $t^{n}+1$
admits a divisor of order k in
$t^{n}+1$
admits a divisor of order k in
![]() $\mathbb {Z}_{2}[t]$
. An immediate way to proceed is to study how
$\mathbb {Z}_{2}[t]$
. An immediate way to proceed is to study how
![]() $t^{n}+1$
can be factorised in irreducible polynomials.
$t^{n}+1$
can be factorised in irreducible polynomials.
Let
![]() $n=2^{a}b$
, with
$n=2^{a}b$
, with
![]() $\gcd (2,b)=1$
. Since we are in characteristic
$\gcd (2,b)=1$
. Since we are in characteristic
![]() $2$
,
$2$
,
Furthermore, if
![]() $\lambda _{d}(t)\in \mathbb {Z}[t]$
denotes the dth cyclotomic polynomial, then
$\lambda _{d}(t)\in \mathbb {Z}[t]$
denotes the dth cyclotomic polynomial, then
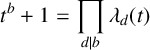 $$ \begin{align*} t^{b}+1 = \prod_{d|b} \lambda_{d}(t) \end{align*} $$
$$ \begin{align*} t^{b}+1 = \prod_{d|b} \lambda_{d}(t) \end{align*} $$
is the factorisation of
![]() $t^{b}+1$
in irreducible polynomials over
$t^{b}+1$
in irreducible polynomials over
![]() $\mathbb {Q}[t]$
, by Gauss’ theorem. Since the Galois group of any field extension of
$\mathbb {Q}[t]$
, by Gauss’ theorem. Since the Galois group of any field extension of
![]() $\mathbb {Z}_{2}$
is a cyclic group generated by the Frobenius automorphism, the degree of an irreducible factor of
$\mathbb {Z}_{2}$
is a cyclic group generated by the Frobenius automorphism, the degree of an irreducible factor of
![]() $\lambda _{d}(t)$
in
$\lambda _{d}(t)$
in
![]() $\mathbb {Z}_{2}[t]$
is the smallest c such that a dth primitive root
$\mathbb {Z}_{2}[t]$
is the smallest c such that a dth primitive root
![]() $\zeta $
raised to the power
$\zeta $
raised to the power
![]() $2^{c}$
is
$2^{c}$
is
![]() $\zeta $
, that is,
$\zeta $
, that is,
![]() $\omega (d)$
. Hence,
$\omega (d)$
. Hence,
![]() $\lambda _{d}(t)$
in
$\lambda _{d}(t)$
in
![]() $\mathbb {Z}_{2}[t]$
factorises into
$\mathbb {Z}_{2}[t]$
factorises into
![]() $\varphi (d)/\omega (d)$
irreducible polynomials, each having degree
$\varphi (d)/\omega (d)$
irreducible polynomials, each having degree
![]() $\omega (d)$
.
$\omega (d)$
.
Therefore,
![]() $t^{n}+1\in \mathbb {Z}_{2}[t]$
has a divisor of degree k if and only if k can be written as the sum of some
$t^{n}+1\in \mathbb {Z}_{2}[t]$
has a divisor of degree k if and only if k can be written as the sum of some
![]() $\omega (d)$
terms, each summand repeated at most
$\omega (d)$
terms, each summand repeated at most
![]() $2^{a}\varphi (d)/\omega (d)$
times, which is exactly (1.2).
$2^{a}\varphi (d)/\omega (d)$
times, which is exactly (1.2).



