Hostname: page-component-76fb5796d-wq484 Total loading time: 0 Render date: 2024-04-27T01:14:21.963Z Has data issue: false hasContentIssue false
  • English
  • Français

$\boldsymbol {L^{p}}$ REGULARITY OF THE SZEGÖ PROJECTION ON THE SYMMETRISED POLYDISC

Part of: Holomorphic functions of several complex variables Harmonic analysis in several variables

Published online by Cambridge University Press:  12 May 2022

KAIKAI HAN Open the ORCID record for KAIKAI HAN [Opens in a new window]  and
YANYAN TANG Open the ORCID record for YANYAN TANG [Opens in a new window]
KAIKAI HAN
Affiliation:
School of Mathematics and Statistics, Hebei University of Economics and Business, Shijiazhuang 050061, PR China e-mail: kkhan.math@whu.edu.cn
YANYAN TANG*
Affiliation:
School of Mathematics and Statistics, Henan University, Kaifeng 475000, PR China
*
e-mail: yanyantang@whu.edu.cn
Get access Rights & Permissions [Opens in a new window]

Abstract

We consider the 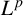$L^{p}$ -regularity of the Szegö projection on the symmetrised polydisc 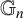$\mathbb {G}_{n}$ . In the setting of the Hardy space corresponding to the distinguished boundary of the symmetrised polydisc, it is shown that this operator is 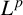$L^{p}$ -bounded for $p\in (2-{1}/{n}, 2+{1}/{(n-1)})$ .

Keywords

L p-regularitysymmetrised polydiscSzegö projection

MSC classification

Primary: 32A36: Bergman spaces
Secondary: 32A25: Integral representations; canonical kernels (Szegő, Bergman, etc.) 42B30: $H^p$-spaces
Type
Research Article
Information
Bulletin of the Australian Mathematical Society , Volume 106 , Issue 3 , December 2022 , pp. 481 - 490
Check for updates
Copyright
© The Author(s), 2022. Published by Cambridge University Press on behalf of Australian Mathematical Publishing Association Inc.

Access options

Get access to the full version of this content by using one of the access options below. (Log in options will check for institutional or personal access. Content may require purchase if you do not have access.)

Footnotes

K.H. is supported by the National Natural Science Foundation of China (Grant No. 12101179) and Scientific Research and Development Program of Hebei University of Economics and Business, PR China (2021QN01). Y.T. is supported by the National Natural Science Foundation of China (Grant No. 12101185).

References

Barrett, D. E., ‘A floating body approach to Fefferman’s hypersurface measure’, Math. Scand. 98(1) (2006), 69–80.10.7146/math.scand.a-14984CrossRefGoogle Scholar
Békollé, D. and Bonami, A., ‘Estimates for the Bergman and Szegö projections in two symmetric domains of ${\mathbb{C}}^n$ ’, Colloq. Math. 68(1) (1995), 81–100.10.4064/cm-68-1-81-100CrossRefGoogle Scholar
Bell, S., ‘The Bergman kernel function and proper holomorphic mappings’, Trans. Amer. Math. Soc. 270(2) (1982), 685–691.Google Scholar
Charpentier, P. and Dupain, Y., ‘Estimates for the Bergman and Szegö projections for pseudoconvex domains of finite type with locally diagonalizable Levi form’, Publ. Mat. 50(2) (2006), 413–446.10.5565/PUBLMAT_50206_08CrossRefGoogle Scholar
Chen, L., Krantz, S. G. and Yuan, Y., ‘ ${L}^p$ regularity of the Bergman projection on domains covered by the polydisc’, J. Funct. Anal. 279(2) (2020), Article no. 108522, 20 pages.CrossRefGoogle Scholar
Costara, C., ‘The symmetrised bidisc and Lempert’s theorem’, Bull. Lond. Math. Soc. 36(5) (2004), 656–662.10.1112/S0024609304003200CrossRefGoogle Scholar
Edigarian, A. and Zwonek, W., ‘Geometry of the symmetrised polydisc’, Arch. Math. (Basel) 84(4) (2005), 364–374.10.1007/s00013-004-1183-zCrossRefGoogle Scholar
Garnett, J. B., Bounded Analytic Functions (Academic Press, New York–London, 1981).Google Scholar
Grellier, S. and Peloso, M. M., ‘Decomposition theorems for Hardy spaces on convex domains of finite type’, Illinois J. Math. 46(1) (2002), 207–232.10.1215/ijm/1258136151CrossRefGoogle Scholar
Jarnicki, M. and Pflug, P., Invariant Distances and Metrics in Complex Analysis, 2nd extended edn, De Gruyter Expositions in Mathematics, 9 (De Gruyter, Berlin, 2013).CrossRefGoogle Scholar
Lanzani, L. and Stein, E. M., ‘Szegö and Bergman projections on non-smooth planar domains’, J. Geom. Anal. 14(1) (2004), 63–86.CrossRefGoogle Scholar
Lanzani, L. and Stein, E. M., ‘The Cauchy–Szegö projection for domains in ${\mathbb{C}}^n$ with minimal smoothness’, Duke Math. J. 166(1) (2017), 125–176.CrossRefGoogle Scholar
McNeal, J. D. and Stein, E. M., ‘The Szegö projection on convex domains’, Math. Z. 224(4) (1997), 519–553.CrossRefGoogle Scholar
Misra, G., Roy, S. S. and Zhang, G., ‘Reproducing kernel for a class of weighted Bergman spaces on the symmetrised polydisc’, Proc. Amer. Math. Soc. 141(7) (2013), 2361–2370.10.1090/S0002-9939-2013-11514-5CrossRefGoogle Scholar
Monguzzi, A. and Peloso, M. M., ‘Sharp estimates for the Szegö projection on the distinguished boundary of model worm domains’, Integral Equations Operator Theory 89(3) (2017), 315–344.10.1007/s00020-017-2405-7CrossRefGoogle Scholar
Munasinghe, S. and Zeytuncu, Y. E., ‘ ${L}^p$ regularity of weighted Szegö projections on the unit disc’, Pacific J. Math. 276(2) (2015), 449–458.10.2140/pjm.2015.276.449CrossRefGoogle Scholar
Phong, D. H. and Stein, E. M., ‘Estimates for the Bergman and Szegö projections on strongly pseudoconvex domains’, Duke Math. J. 44(3) (1977), 695–704.CrossRefGoogle Scholar
Rudin, W., Function Theory in Polydiscs (Benjamin, New York, 1969).Google Scholar
Rudin, W., ‘Proper holomorphic maps and finite reflection groups’, Indiana Univ. Math. J. 31 (1982), 701–720.10.1512/iumj.1982.31.31050CrossRefGoogle Scholar
Stein, E. M., Boundary Behavior of Holomorphic Functions of Several Complex Variables, Mathematical Notes, 11 (Princeton University Press–University of Tokyo Press, Princeton, NJ–Tokyo, 1972).Google Scholar
Zhu, K., Operator Theory in Function Spaces (Marcel Dekker, New York, 1990).Google Scholar