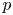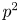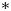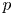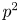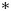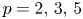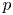1. Introduction
A supercharacter theory of a finite group is a somewhat condensed form of its character theory where the conjugacy classes are replaced by certain unions of conjugacy classes and the irreducible characters are replaced by certain pairwise orthogonal characters that are constant on the superclasses. In essence, a supercharacter theory is an approximation of the representation theory that preserves much of the duality exhibited by conjugacy classes and irreducible characters. Supercharacter theory has proven useful in a variety of situations where the full character theory is unable to be described in a useful combinatorial way.
The problem of classifying all supercharacter theories of a given finite group appears to be a difficult problem. For example, in [Reference Burkett, Lamar, Lewis and Wynn6], the authors saw no way other than to use a computer program to show that $\mathrm {Sp}_6(\mathbb {F}_2)$![]() has exactly two supercharacter theories. The problem of classifying all supercharacter theories of a family of finite groups seems likely to be much more difficult. At this time, we know of only a few families of groups for which this has been done; only one of which consists of non-abelian groups.
has exactly two supercharacter theories. The problem of classifying all supercharacter theories of a family of finite groups seems likely to be much more difficult. At this time, we know of only a few families of groups for which this has been done; only one of which consists of non-abelian groups.
In his Ph.D. thesis [Reference Hendrickson9], Hendrickson classified the supercharacter theories of cyclic $p$![]() -groups. It is then explained in the subsequent paper [Reference Hendrickson10] that the supercharacter theories of cyclic groups had already been classified by Leung and Man under the guise of Schur rings (see [Reference Leung and Man16, Reference Leung and Man17]). In [Reference Hendrickson10], it is shown that the set of supercharacter theories of a group are in bijection with the set of central S-rings of the group. In fact, the Schur rings of cyclic $p$
-groups. It is then explained in the subsequent paper [Reference Hendrickson10] that the supercharacter theories of cyclic groups had already been classified by Leung and Man under the guise of Schur rings (see [Reference Leung and Man16, Reference Leung and Man17]). In [Reference Hendrickson10], it is shown that the set of supercharacter theories of a group are in bijection with the set of central S-rings of the group. In fact, the Schur rings of cyclic $p$![]() -groups were classified even earlier. (See [Reference Pöschel20] for the odd prime case and [Reference Ch. Klin, Najmark and Pöschel12, Reference Kovács13] for the cyclic $2$
-groups were classified even earlier. (See [Reference Pöschel20] for the odd prime case and [Reference Ch. Klin, Najmark and Pöschel12, Reference Kovács13] for the cyclic $2$![]() -groups.) The supercharacter theories of the groups $C_2\times C_2\times C_p$
-groups.) The supercharacter theories of the groups $C_2\times C_2\times C_p$![]() for $p$
for $p$![]() a prime were classified in [Reference Evdokimov, Kovács and Ponomarenko8] (again via Schur rings).
a prime were classified in [Reference Evdokimov, Kovács and Ponomarenko8] (again via Schur rings).
The supercharacter theories of the dihedral groups have been classified several times. Wynn classified the supercharacter theories of dihedral groups in his Ph.D. thesis [Reference Wynn24]. They were also classified by Lamar in his Ph.D. thesis [Reference Lamar15] (see also the preprint [Reference Lamar14]), where the properties of the lattice of supercharacter theories are also studied. It turns out that the supercharacter theories of the dihedral groups of order twice a prime were classified previously by Wai-Chee [Reference Shiu21], where their Schur rings were studied (supercharacter theories correspond to the central Schur rings). Finally, we mention that Wynn and the second author classified the supercharacter theories of Frobenius groups of order $pq$![]() in [Reference Lewis and Wynn18] and also reduced the problem of classifying the supercharacter theories of Frobenius groups and semi-extraspecial groups to classifying the supercharacter theories of various quotients and subgroups.
in [Reference Lewis and Wynn18] and also reduced the problem of classifying the supercharacter theories of Frobenius groups and semi-extraspecial groups to classifying the supercharacter theories of various quotients and subgroups.
Each of the above classifications involves certain supercharacter theory products, including $\ast$![]() and direct products, which will be described explicitly in § 2. Each of the above classifications also involves supercharacter theories coming from automorphisms — those constructed from the action of a group by automorphisms. The purpose of this paper is to study the supercharacter theories of the elementary abelian group $C_p\times C_p$
and direct products, which will be described explicitly in § 2. Each of the above classifications also involves supercharacter theories coming from automorphisms — those constructed from the action of a group by automorphisms. The purpose of this paper is to study the supercharacter theories of the elementary abelian group $C_p\times C_p$![]() , where $p$
, where $p$![]() is a prime. The first thing to notice is that a classification of the supercharacter theories of $C_p\times C_p$
is a prime. The first thing to notice is that a classification of the supercharacter theories of $C_p\times C_p$![]() would not need to include the above supercharacter theory products.
would not need to include the above supercharacter theory products.
Theorem A. Every supercharacter theory of $C_p\times C_p$![]() that can be realized as a $\ast$
that can be realized as a $\ast$![]() -product or direct product comes from automorphisms.
-product or direct product comes from automorphisms.
Although we do not give a full classification, we will classify certain types of supercharacter theories. Specifically, we prove the following:
Theorem B. Any supercharacter theory $\mathsf {S}$![]() of the elementary abelian group $C_p\times C_p$
of the elementary abelian group $C_p\times C_p$![]() that has a non-identity superclass of size one or a non-principal linear supercharacter comes from a supercharacter theory ($\ast$
that has a non-identity superclass of size one or a non-principal linear supercharacter comes from a supercharacter theory ($\ast$![]() or direct) product. In particular, $\mathsf {S}$
or direct) product. In particular, $\mathsf {S}$![]() comes from automorphisms.
comes from automorphisms.
In § 5, we show that any partition of the non-trivial, proper subgroups of $C_p\times C_p$![]() gives rise to a supercharacter theory and that these partition supercharacter theories play a special role in the full lattice of supercharacter theories. In § 6, we make a strong conjecture regarding the structure of certain types of supercharacter theories that has been supported through computational evidence. Although we do not provide a full classification, we believe this paper to be a good starting point for anyone who desires to do so. We mention that we are able to provide a full classification for the prime $p=2,\,3$
gives rise to a supercharacter theory and that these partition supercharacter theories play a special role in the full lattice of supercharacter theories. In § 6, we make a strong conjecture regarding the structure of certain types of supercharacter theories that has been supported through computational evidence. Although we do not provide a full classification, we believe this paper to be a good starting point for anyone who desires to do so. We mention that we are able to provide a full classification for the prime $p=2,\,3$![]() and $5$
and $5$![]() . Using the work in [Reference Ziv-Av25, 26], we obtain a similar classification for $p = 7$
. Using the work in [Reference Ziv-Av25, 26], we obtain a similar classification for $p = 7$![]() .
.
We would like to thank Professor Ilia Ponomarenko for mentioning references [Reference Ch. Klin, Najmark and Pöschel12, Reference Kovács13, Reference Pöschel20, Reference van Dam and Muzychuk22, Reference Ziv-Av25] to us.
2. Preliminaries
Diaconis and Isaacs [Reference Diaconis and Isaacs7] define a supercharacter theory to be a pair $(\mathcal {X},\,\mathcal {K})$![]() , where $\mathcal {X}$
, where $\mathcal {X}$![]() is a partition of $\mathrm {Irr}(G)$
is a partition of $\mathrm {Irr}(G)$![]() and $\mathcal {K}$
and $\mathcal {K}$![]() is a partition of $G$
is a partition of $G$![]() satisfying the following three conditions:
satisfying the following three conditions:
• $\lvert{\mathcal {X}}\rvert=\lvert {\mathcal {K}}\rvert$
 ;
;• $\{1\}\in \mathcal {K}$
 ;
;• For every $X\in \mathcal {X}$
 , there is a character $\xi _X$
, there is a character $\xi _X$ whose constituents lie in $X$
whose constituents lie in $X$ that is constant on the parts of $\mathcal {K}$
that is constant on the parts of $\mathcal {K}$ .
.
For each $X\in \mathcal {X}$![]() , the character $\xi _X$
, the character $\xi _X$![]() is a constant multiple of the character $\sigma _X=\sum \nolimits _{\psi \in X}\psi (1)\psi$
is a constant multiple of the character $\sigma _X=\sum \nolimits _{\psi \in X}\psi (1)\psi$![]() . We let $\mathrm {BCh}(\mathsf {S})=\{\sigma _X:X\in \mathcal {X}\}$
. We let $\mathrm {BCh}(\mathsf {S})=\{\sigma _X:X\in \mathcal {X}\}$![]() and call its elements the basic $\mathsf {S}$
and call its elements the basic $\mathsf {S}$![]() -characters. If $\mathsf {S}=(\mathcal {X},\,\mathcal {K})$
-characters. If $\mathsf {S}=(\mathcal {X},\,\mathcal {K})$![]() is a supercharacter theory, we write $\mathcal {K}=\mathrm {Cl}(\mathsf {S})$
is a supercharacter theory, we write $\mathcal {K}=\mathrm {Cl}(\mathsf {S})$![]() and call its elements $\mathsf {S}$
and call its elements $\mathsf {S}$![]() -classes. The principal character of $G$
-classes. The principal character of $G$![]() is always a basic $\mathsf {S}$
is always a basic $\mathsf {S}$![]() -character. When there is no ambiguity, we may refer to $\mathsf {S}$
-character. When there is no ambiguity, we may refer to $\mathsf {S}$![]() -classes and basic $\mathsf {S}$
-classes and basic $\mathsf {S}$![]() -characters as superclasses and supercharacters. We will frequently make use of the fact that $\mathsf {S}$
-characters as superclasses and supercharacters. We will frequently make use of the fact that $\mathsf {S}$![]() -classes and basic $\mathsf {S}$
-classes and basic $\mathsf {S}$![]() -characters uniquely determine each other [Reference Diaconis and Isaacs7, Theorem 2.2 (c)].
-characters uniquely determine each other [Reference Diaconis and Isaacs7, Theorem 2.2 (c)].
The set $\mathrm {SCT}(G)$![]() of all supercharacter theories comes equipped with a partial order. Hendrickson [Reference Hendrickson10] shows that for any two supercharacter theories $\mathsf {S}$
of all supercharacter theories comes equipped with a partial order. Hendrickson [Reference Hendrickson10] shows that for any two supercharacter theories $\mathsf {S}$![]() and $\mathsf {T}$
and $\mathsf {T}$![]() , every $\mathsf {T}$
, every $\mathsf {T}$![]() -class is a union of $\mathsf {S}$
-class is a union of $\mathsf {S}$![]() -classes if and only if every basic $\mathsf {T}$
-classes if and only if every basic $\mathsf {T}$![]() -character is a sum of basic $\mathsf {S}$
-character is a sum of basic $\mathsf {S}$![]() -characters. In this event, we write $\mathsf {S}\preccurlyeq \mathsf {T}$
-characters. In this event, we write $\mathsf {S}\preccurlyeq \mathsf {T}$![]() . We say that $\mathsf {S}$
. We say that $\mathsf {S}$![]() is finer than $\mathsf {T}$
is finer than $\mathsf {T}$![]() or that $\mathsf {T}$
or that $\mathsf {T}$![]() is coarser than $\mathsf {S}$
is coarser than $\mathsf {S}$![]() . Since $\mathrm {SCT}(G)$
. Since $\mathrm {SCT}(G)$![]() has a partial order and a maximal (and minimal) element, it is actually a lattice. The join operation $\vee$
has a partial order and a maximal (and minimal) element, it is actually a lattice. The join operation $\vee$![]() on $\mathrm {SCT}(G)$
on $\mathrm {SCT}(G)$![]() is very well behaved and is inherited from the join operation on the set of partitions of $G$
is very well behaved and is inherited from the join operation on the set of partitions of $G$![]() under the refinement order, which we will also denote by $\vee$
under the refinement order, which we will also denote by $\vee$![]() . If $\mathsf {S}$
. If $\mathsf {S}$![]() and $\mathsf {T}$
and $\mathsf {T}$![]() are supercharacter theories of $G$
are supercharacter theories of $G$![]() , then the superclasses of $\mathsf {S}\vee \mathsf {T}$
, then the superclasses of $\mathsf {S}\vee \mathsf {T}$![]() is just the mutual coarsening of the partitions $\mathrm {Cl}(\mathsf {S})$
is just the mutual coarsening of the partitions $\mathrm {Cl}(\mathsf {S})$![]() and $\mathrm {Cl}(\mathsf {T})$
and $\mathrm {Cl}(\mathsf {T})$![]() ; i.e., $\mathrm {Cl}(\mathsf {S})\vee \mathrm {Cl}(\mathsf {T})$
; i.e., $\mathrm {Cl}(\mathsf {S})\vee \mathrm {Cl}(\mathsf {T})$![]() . However, the meet operation $\wedge$
. However, the meet operation $\wedge$![]() on $\mathrm {SCT}(G)$
on $\mathrm {SCT}(G)$![]() is poorly behaved and difficult to compute. In particular, the equation $\mathrm {Cl}(\mathsf {S}\wedge \mathsf {T})=\mathrm {Cl}(\mathsf {S})\wedge \mathrm {Cl}(\mathsf {T})$
is poorly behaved and difficult to compute. In particular, the equation $\mathrm {Cl}(\mathsf {S}\wedge \mathsf {T})=\mathrm {Cl}(\mathsf {S})\wedge \mathrm {Cl}(\mathsf {T})$![]() holds only sporadically. One example where this equality does hold will be discussed later in this section (see Lemma 2.2).
holds only sporadically. One example where this equality does hold will be discussed later in this section (see Lemma 2.2).
Every finite group has two trivial supercharacter theories. The first, which we denote by $\mathsf {m}(G)$![]() , is the supercharacter theory with superclasses the usual conjugacy classes of $G$
, is the supercharacter theory with superclasses the usual conjugacy classes of $G$![]() . The supercharacters of $\mathsf {m}(G)$
. The supercharacters of $\mathsf {m}(G)$![]() are exactly the irreducible characters of $G$
are exactly the irreducible characters of $G$![]() (multiplied by their degrees). This is the finest supercharacter theory of $G$
(multiplied by their degrees). This is the finest supercharacter theory of $G$![]() under the partial order discussed in the previous paragraph (i.e., $\mathsf {m}(G)\preccurlyeq \mathsf {S}$
under the partial order discussed in the previous paragraph (i.e., $\mathsf {m}(G)\preccurlyeq \mathsf {S}$![]() for every supercharacter theory $\mathsf {S}$
for every supercharacter theory $\mathsf {S}$![]() of $G$
of $G$![]() ). There is also a coarsest supercharacter theory of $G$
). There is also a coarsest supercharacter theory of $G$![]() for the partial ordering of the previous paragraph, denoted by $\mathsf {M}(G)$
for the partial ordering of the previous paragraph, denoted by $\mathsf {M}(G)$![]() (i.e., $\mathsf {S}\preccurlyeq \mathsf {M}(G)$
(i.e., $\mathsf {S}\preccurlyeq \mathsf {M}(G)$![]() for every supercharacter theory $\mathsf {S}$
for every supercharacter theory $\mathsf {S}$![]() of $G$
of $G$![]() ). The $\mathsf {M}(G)$
). The $\mathsf {M}(G)$![]() -classes are just $\{1\}$
-classes are just $\{1\}$![]() and $G\setminus \{1\}$
and $G\setminus \{1\}$![]() and the basic $\mathsf {M}(G)$
and the basic $\mathsf {M}(G)$![]() -characters are $\mathbb {1}$
-characters are $\mathbb {1}$![]() and $\rho _G-\mathbb {1}$
and $\rho _G-\mathbb {1}$![]() , where $\mathbb {1}$
, where $\mathbb {1}$![]() is the principal character and $\rho _G$
is the principal character and $\rho _G$![]() is the regular character of $G$
is the regular character of $G$![]() .
.
Supercharacter theories can arise in many different (often mysterious) ways. One of the more well-known ways comes from actions by automorphisms. If $A\le \mathrm {Aut}(G)$![]() , then $A$
, then $A$![]() acts on $\mathrm {Irr}(G)$
acts on $\mathrm {Irr}(G)$![]() via $\chi ^{a}(g)=\chi (g^{a^{-1}})$
via $\chi ^{a}(g)=\chi (g^{a^{-1}})$![]() for $a\in A$
for $a\in A$![]() , $\chi \in \mathrm {Irr}(G)$
, $\chi \in \mathrm {Irr}(G)$![]() and $g\in G$
and $g\in G$![]() . Then Brauer's Permutation Lemma (see [Reference Isaacs11, Theorem 6.32], for example) can be used to show that the orbits of $G$
. Then Brauer's Permutation Lemma (see [Reference Isaacs11, Theorem 6.32], for example) can be used to show that the orbits of $G$![]() and $\mathrm {Irr}(G)$
and $\mathrm {Irr}(G)$![]() under the action of $A$
under the action of $A$![]() yield a supercharacter theory. In this case, we say that $\mathsf {S}$
yield a supercharacter theory. In this case, we say that $\mathsf {S}$![]() comes from $A$
comes from $A$![]() or comes from automorphisms. An important aspect of the Leung–Man classification [Reference Leung and Man16, Reference Leung and Man17] (or Hendrickson's [Reference Hendrickson9]) is that every supercharacter theory of a cyclic group of prime order comes from automorphisms. This fact will be used extensively later without reference.
or comes from automorphisms. An important aspect of the Leung–Man classification [Reference Leung and Man16, Reference Leung and Man17] (or Hendrickson's [Reference Hendrickson9]) is that every supercharacter theory of a cyclic group of prime order comes from automorphisms. This fact will be used extensively later without reference.
Just as every normal subgroup is determined by the conjugacy classes of $G$![]() and by the irreducible characters, there is a distinguished set of normal subgroups determined by a supercharacter theory $\mathsf {S}$
and by the irreducible characters, there is a distinguished set of normal subgroups determined by a supercharacter theory $\mathsf {S}$![]() . Any subgroup $N$
. Any subgroup $N$![]() that is a union of $\mathsf {S}$
that is a union of $\mathsf {S}$![]() -classes is called $\mathsf {S}$
-classes is called $\mathsf {S}$![]() -normal. In this situation, we write $N\lhd _{\mathsf {S}}G$
-normal. In this situation, we write $N\lhd _{\mathsf {S}}G$![]() . It is not difficult to show that $N$
. It is not difficult to show that $N$![]() is the intersection of the kernels of those $\chi \in \mathrm {BCh}(\mathsf {S})$
is the intersection of the kernels of those $\chi \in \mathrm {BCh}(\mathsf {S})$![]() that satisfy $N\le \ker (\chi )$
that satisfy $N\le \ker (\chi )$![]() . In fact, this is another way to classify $\mathsf {S}$
. In fact, this is another way to classify $\mathsf {S}$![]() -normal subgroups [Reference Marberg19].
-normal subgroups [Reference Marberg19].
Whenever $N$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, Hendrickson [Reference Hendrickson10] showed that $\mathsf {S}$
-normal, Hendrickson [Reference Hendrickson10] showed that $\mathsf {S}$![]() gives rise to a supercharacter theory $\mathsf {S}_N$
gives rise to a supercharacter theory $\mathsf {S}_N$![]() of $N$
of $N$![]() and $\mathsf {S}^{G/N}$
and $\mathsf {S}^{G/N}$![]() of $G/N$
of $G/N$![]() . The $\mathsf {S}_N$
. The $\mathsf {S}_N$![]() -classes are just the $\mathsf {S}$
-classes are just the $\mathsf {S}$![]() -classes contained in $N$
-classes contained in $N$![]() and the basic $\mathsf {S}_N$
and the basic $\mathsf {S}_N$![]() -characters are the restrictions of the basic $\mathsf {S}$
-characters are the restrictions of the basic $\mathsf {S}$![]() -characters, up to a constant. Moreover, it is a result of the first author (see [Reference Burkett1, Theorem 1.1.2] or [Reference Burkett3, Theorem A]) that if $\chi \in \mathrm {BCh}(\mathsf {S})$
-characters, up to a constant. Moreover, it is a result of the first author (see [Reference Burkett1, Theorem 1.1.2] or [Reference Burkett3, Theorem A]) that if $\chi \in \mathrm {BCh}(\mathsf {S})$![]() and $\psi$
and $\psi$![]() is the basic-$\mathsf{S}_{\mathsf{N}}$
is the basic-$\mathsf{S}_{\mathsf{N}}$![]() -character lying under $\chi$
-character lying under $\chi$![]() , then $\chi (1)/\psi (1)$
, then $\chi (1)/\psi (1)$![]() is an integer. The $\mathsf {S}^{G/N}$
is an integer. The $\mathsf {S}^{G/N}$![]() -classes are the images of the $\mathsf {S}$
-classes are the images of the $\mathsf {S}$![]() -classes under the canonical projection $G\to G/N$
-classes under the canonical projection $G\to G/N$![]() and the basic $\mathsf {S}^{G/N}$
and the basic $\mathsf {S}^{G/N}$![]() -characters can be identified with the basic $\mathsf {S}$
-characters can be identified with the basic $\mathsf {S}$![]() -characters with $N$
-characters with $N$![]() contained in their kernel. These constructions are compatible in the sense that $(\mathsf {S}_N)^{N/M}=(\mathsf {S}^{G/M})_{N/M}$
contained in their kernel. These constructions are compatible in the sense that $(\mathsf {S}_N)^{N/M}=(\mathsf {S}^{G/M})_{N/M}$![]() . As such, we simply write $\mathsf {S}_{N/M}$
. As such, we simply write $\mathsf {S}_{N/M}$![]() in this situation. In [Reference Burkett2], the first author shows that these constructions respect the lattice structure of the set of $\mathsf {S}$
in this situation. In [Reference Burkett2], the first author shows that these constructions respect the lattice structure of the set of $\mathsf {S}$![]() -normal subgroups. In particular, if $H$
-normal subgroups. In particular, if $H$![]() and $N$
and $N$![]() are any $\mathsf {S}$
are any $\mathsf {S}$![]() -normal subgroups, then the images of the superclasses of $\mathsf {S}_{H/(H\cap N)}$
-normal subgroups, then the images of the superclasses of $\mathsf {S}_{H/(H\cap N)}$![]() under the canonical isomorphism $H/(H\cap N)\to HN/N$
under the canonical isomorphism $H/(H\cap N)\to HN/N$![]() are exactly the $\mathsf {S}_{HN/N}$
are exactly the $\mathsf {S}_{HN/N}$![]() -classes [Reference Burkett2, Theorem A].
-classes [Reference Burkett2, Theorem A].
Hendrickson also used these constructions to define supercharacter theories of the full group. Given any supercharacter theory $\mathsf {U}$![]() of a normal subgroup $N$
of a normal subgroup $N$![]() of $G$
of $G$![]() whose superclasses are fixed (set-wise) under the conjugation action of $G$
whose superclasses are fixed (set-wise) under the conjugation action of $G$![]() and a supercharacter theory $\mathsf {V}$
and a supercharacter theory $\mathsf {V}$![]() of $G/N$
of $G/N$![]() , Hendrickson defines the $\ast$
, Hendrickson defines the $\ast$![]() -product $\mathsf {U}\ast \mathsf {V}$
-product $\mathsf {U}\ast \mathsf {V}$![]() as follows. The supercharacters of $\mathsf {U}\ast \mathsf {V}$
as follows. The supercharacters of $\mathsf {U}\ast \mathsf {V}$![]() that have $N$
that have $N$![]() in their kernel can be naturally identified with the supercharacters in $\mathrm {BCh}(\mathsf {V})$
in their kernel can be naturally identified with the supercharacters in $\mathrm {BCh}(\mathsf {V})$![]() and those that do not have $N$
and those that do not have $N$![]() in their kernel are just induced from non-principal members of $\mathrm {BCh}(\mathsf {U})$
in their kernel are just induced from non-principal members of $\mathrm {BCh}(\mathsf {U})$![]() . The superclasses of $\mathsf {U}\ast \mathsf {V}$
. The superclasses of $\mathsf {U}\ast \mathsf {V}$![]() contained in $N$
contained in $N$![]() are the superclasses of $\mathsf {U}$
are the superclasses of $\mathsf {U}$![]() , and the superclasses of $\mathsf {U}\ast \mathsf {V}$
, and the superclasses of $\mathsf {U}\ast \mathsf {V}$![]() lying outside of $N$
lying outside of $N$![]() are the full preimages of the non-identity superclasses of $\mathsf {V}$
are the full preimages of the non-identity superclasses of $\mathsf {V}$![]() under the canonical projection $G\to G/N$
under the canonical projection $G\to G/N$![]() . If $\mathsf {S}$
. If $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() and $N\lhd _{\mathsf {S}}G$
and $N\lhd _{\mathsf {S}}G$![]() , then $\mathsf {S}\preccurlyeq \mathsf {S}_N\ast \mathsf {S}_{G/N}$
, then $\mathsf {S}\preccurlyeq \mathsf {S}_N\ast \mathsf {S}_{G/N}$![]() , with equality if and only if every $\mathsf {S}$
, with equality if and only if every $\mathsf {S}$![]() -class lying outside of $N$
-class lying outside of $N$![]() is a union of $N$
is a union of $N$![]() -cosets.
-cosets.
Another characterization that appears in [Reference Burkett and Lewis5] is the following. Let $N$![]() be $\mathsf {S}$
be $\mathsf {S}$![]() -normal. Then $\mathsf {S}$
-normal. Then $\mathsf {S}$![]() is a $\ast$
is a $\ast$![]() -product over $N$
-product over $N$![]() if and only if every $\chi \in \mathrm {BCh}(\mathsf {S})$
if and only if every $\chi \in \mathrm {BCh}(\mathsf {S})$![]() satisfying $N\nleq \ker (\chi )$
satisfying $N\nleq \ker (\chi )$![]() vanishes on $G\setminus N$
vanishes on $G\setminus N$![]() . One direction of this result follows easily from the next lemma about basic $\mathsf {S}$
. One direction of this result follows easily from the next lemma about basic $\mathsf {S}$![]() -characters vanishing off $\mathsf {S}$
-characters vanishing off $\mathsf {S}$![]() -normal subgroups.
-normal subgroups.
Lemma 2.1 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() and let $\chi \in \mathrm {BCh}(\mathsf {S})$
and let $\chi \in \mathrm {BCh}(\mathsf {S})$![]() . Assume that $\chi$
. Assume that $\chi$![]() vanishes on $G\setminus N$
vanishes on $G\setminus N$![]() , where $N$
, where $N$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal. Then $\chi =\psi ^{G}$
-normal. Then $\chi =\psi ^{G}$![]() for some basic $\mathsf {S}_N$
for some basic $\mathsf {S}_N$![]() - character $\psi$
- character $\psi$![]() .
.
Proof. Since $\mathsf {S}\preccurlyeq \mathsf {S}_N\ast \mathsf {S}_{G/N}$![]() , $\psi ^{G}$
, $\psi ^{G}$![]() is a sum of distinct basic $\mathsf {S}$
is a sum of distinct basic $\mathsf {S}$![]() -characters. Let $\xi$
-characters. Let $\xi$![]() be one such basic $\mathsf {S}$
be one such basic $\mathsf {S}$![]() -character, and note that $\chi _N=\frac {\chi (1)}{\psi (1)}\psi$
-character, and note that $\chi _N=\frac {\chi (1)}{\psi (1)}\psi$![]() . Then
. Then

The result easily follows.
Also defined in [Reference Hendrickson10] is the direct product of supercharacter theories. Given a supercharacter theory $\mathsf {E}$![]() of a group $H$
of a group $H$![]() and a supercharacter theory $\mathsf {F}$
and a supercharacter theory $\mathsf {F}$![]() of a group $K$
of a group $K$![]() , the supercharacter theory $\mathsf {E}\times \mathsf {F}$
, the supercharacter theory $\mathsf {E}\times \mathsf {F}$![]() of $H\times K$
of $H\times K$![]() is defined by $\mathrm {Cl}(\mathsf {E}\times \mathsf {F})=\{K\times L:K\in \mathrm {Cl}(\mathsf {E}),\,\ L\in \mathrm {Cl}(\mathsf {F})\}$
is defined by $\mathrm {Cl}(\mathsf {E}\times \mathsf {F})=\{K\times L:K\in \mathrm {Cl}(\mathsf {E}),\,\ L\in \mathrm {Cl}(\mathsf {F})\}$![]() and $\mathrm {BCh}(\mathsf {E}\times \mathsf {F})=\{\chi \times \xi :\chi \in \mathrm {BCh}(\mathsf {E}),\,\ \xi \in \mathrm {BCh}(\mathsf {F})\}$
and $\mathrm {BCh}(\mathsf {E}\times \mathsf {F})=\{\chi \times \xi :\chi \in \mathrm {BCh}(\mathsf {E}),\,\ \xi \in \mathrm {BCh}(\mathsf {F})\}$![]() . The direct product supercharacter theory is intimately related to the $\ast$
. The direct product supercharacter theory is intimately related to the $\ast$![]() -product, as this next result illustrates.
-product, as this next result illustrates.
Lemma 2.2 Let $G=H\times N$![]() , let $\mathsf {S}\in \mathrm {SCT}(H),$
, let $\mathsf {S}\in \mathrm {SCT}(H),$![]() and let $\mathsf {T}\in \mathrm {SCT}(N)$
and let $\mathsf {T}\in \mathrm {SCT}(N)$![]() . Let $\varphi _1:H\to G/N$
. Let $\varphi _1:H\to G/N$![]() and $\varphi _2:N\to G/H$
and $\varphi _2:N\to G/H$![]() be the projections. Let $\tilde {\mathsf {S}}=\varphi _1(\mathsf {S})\in \mathrm {SCT}(G/N),$
be the projections. Let $\tilde {\mathsf {S}}=\varphi _1(\mathsf {S})\in \mathrm {SCT}(G/N),$![]() and let $\tilde {\mathsf {T}}=\varphi _2(\mathsf {T})\in \mathrm {SCT}(G/H)$
and let $\tilde {\mathsf {T}}=\varphi _2(\mathsf {T})\in \mathrm {SCT}(G/H)$![]() . Write $\mathsf {U}=\mathsf {S}\ast \tilde {T}$
. Write $\mathsf {U}=\mathsf {S}\ast \tilde {T}$![]() and $\mathsf {V}=\mathsf {T}\ast \tilde {S}$
and $\mathsf {V}=\mathsf {T}\ast \tilde {S}$![]() . Then $\mathrm {Cl}(\mathsf {S}\times \mathsf {T})=\mathrm {Cl}(\mathsf {U})\wedge \mathrm {Cl}(\mathsf {V})$
. Then $\mathrm {Cl}(\mathsf {S}\times \mathsf {T})=\mathrm {Cl}(\mathsf {U})\wedge \mathrm {Cl}(\mathsf {V})$![]() . In particular, $\mathsf {S}\times \mathsf {T}$
. In particular, $\mathsf {S}\times \mathsf {T}$![]() is equal to $\mathsf {U}\wedge \mathsf {V}$
is equal to $\mathsf {U}\wedge \mathsf {V}$![]() .
.
Proof. We have
and
The mutual refinement of these partitions is exactly
Since $\mathcal {K}$![]() is the set of superclasses of a supercharacter theory of $G$
is the set of superclasses of a supercharacter theory of $G$![]() , and $\mathcal {K}$
, and $\mathcal {K}$![]() is the coarsest partition of $G$
is the coarsest partition of $G$![]() finer than both $\mathrm {Cl}(\mathsf {U})$
finer than both $\mathrm {Cl}(\mathsf {U})$![]() and $\mathrm {Cl}(\mathsf {T})$
and $\mathrm {Cl}(\mathsf {T})$![]() , it follows that $\mathcal {K}=\mathrm {Cl}(\mathsf {U}\wedge \mathsf {V})$
, it follows that $\mathcal {K}=\mathrm {Cl}(\mathsf {U}\wedge \mathsf {V})$![]() , which means $\mathsf {U}\wedge \mathsf {V}=\mathsf {S}\times \mathsf {T}$
, which means $\mathsf {U}\wedge \mathsf {V}=\mathsf {S}\times \mathsf {T}$![]() .
.
Recall that $\mathsf {S}\preccurlyeq \mathsf {S}_N\ast \mathsf {S}_{G/N}$![]() whenever $N$
whenever $N$![]() is an $\mathsf {S}$
is an $\mathsf {S}$![]() -normal subgroup of $G$
-normal subgroup of $G$![]() . Thus, as an immediate corollary of Lemma 2.2, we deduce the following.
. Thus, as an immediate corollary of Lemma 2.2, we deduce the following.
Corollary 2.3 Let $G=H\times N$![]() and suppose $\mathsf {S}$
and suppose $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() in which both $H$
in which both $H$![]() and $N$
and $N$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -normal. Then $\mathsf {S}\preccurlyeq \mathsf {S}_H\times \mathsf {S}_N,$
-normal. Then $\mathsf {S}\preccurlyeq \mathsf {S}_H\times \mathsf {S}_N,$![]() with equality if and only if $\lvert {\mathsf {S}}\rvert=\lvert {\mathsf {S}_H}\rvert \cdot \lvert {\mathsf {S}_N}\rvert$
with equality if and only if $\lvert {\mathsf {S}}\rvert=\lvert {\mathsf {S}_H}\rvert \cdot \lvert {\mathsf {S}_N}\rvert$![]() .
.
Proof. Using the notation in the statement of the previous result, we have $\widetilde {\mathsf {S}_H}=\mathsf {S}_{G/N}$![]() and $\widetilde {\mathsf {S}_N}=\mathsf {S}_{G/H}$
and $\widetilde {\mathsf {S}_N}=\mathsf {S}_{G/H}$![]() [Reference Burkett2, Theorem A]. Since
[Reference Burkett2, Theorem A]. Since
and
we have
Since $\mathsf {S}\preccurlyeq \mathsf {S}_H\times \mathsf {S}_N$![]() and $\lvert {\mathsf {S}_H\times \mathsf {S}_N}\rvert=\lvert {\mathsf {S}_H}\rvert\cdot \lvert {\mathsf {S}_N}\rvert$
and $\lvert {\mathsf {S}_H\times \mathsf {S}_N}\rvert=\lvert {\mathsf {S}_H}\rvert\cdot \lvert {\mathsf {S}_N}\rvert$![]() , the result follows.
, the result follows.
We mention one more construction we will need, also due to Hendrickson. If $G$![]() is an abelian group, then $\mathrm {Irr}(G)$
is an abelian group, then $\mathrm {Irr}(G)$![]() forms a group under the pointwise product. There is a natural isomorphism $G\to \mathrm {Irr}(\mathrm {Irr}(G))$
forms a group under the pointwise product. There is a natural isomorphism $G\to \mathrm {Irr}(\mathrm {Irr}(G))$![]() sending $g\in G$
sending $g\in G$![]() to $\tilde {g}\in \mathrm {Irr}(\mathrm {Irr}(G))$
to $\tilde {g}\in \mathrm {Irr}(\mathrm {Irr}(G))$![]() defined by $\tilde {g}(\chi )=\chi (g)$
defined by $\tilde {g}(\chi )=\chi (g)$![]() . If $\mathsf {S}$
. If $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() , then ${\check {\mathsf {S}}}$
, then ${\check {\mathsf {S}}}$![]() is a supercharacter theory of $\mathrm {Irr}(G)$
is a supercharacter theory of $\mathrm {Irr}(G)$![]() , where $\mathrm {Cl}({\check {\mathsf {S}}})=\mathrm {BCh}(\mathsf {S})$
, where $\mathrm {Cl}({\check {\mathsf {S}}})=\mathrm {BCh}(\mathsf {S})$![]() and $\mathrm {BCh}({\check {\mathsf {S}}})=\{\{\tilde {g}:g\in K\}:K\in \mathrm {Cl}(\mathsf {S})\}$
and $\mathrm {BCh}({\check {\mathsf {S}}})=\{\{\tilde {g}:g\in K\}:K\in \mathrm {Cl}(\mathsf {S})\}$![]() [Reference Hendrickson9, Theorem 5.3]. This duality construction will be used to simplify some arguments in the proof of Theorem B.
[Reference Hendrickson9, Theorem 5.3]. This duality construction will be used to simplify some arguments in the proof of Theorem B.
3. Central elements and commutators
Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() . In [Reference Burkett3], the first author discusses two important subgroups of $G$
. In [Reference Burkett3], the first author discusses two important subgroups of $G$![]() associated with $\mathsf {S}$
associated with $\mathsf {S}$![]() . The first of these subgroups is an analog of the centre of a group and consists of the superclasses of size one. We denote this subgroup by $Z(\mathsf {S})$
. The first of these subgroups is an analog of the centre of a group and consists of the superclasses of size one. We denote this subgroup by $Z(\mathsf {S})$![]() . The fact that $Z(\mathsf {S})$
. The fact that $Z(\mathsf {S})$![]() is a ($\mathsf {S}$
is a ($\mathsf {S}$![]() -normal) subgroup follows easily from [Reference Diaconis and Isaacs7, Corollary 2.3] and a proof appears in [Reference Hendrickson9]. Another consequence of [Reference Diaconis and Isaacs7, Corollary 2.3] appearing in [Reference Hendrickson9] is that $\mathrm {cl}_{\mathsf {S}}(g)z=\mathrm {cl}_{\mathsf {S}}(gz)$
-normal) subgroup follows easily from [Reference Diaconis and Isaacs7, Corollary 2.3] and a proof appears in [Reference Hendrickson9]. Another consequence of [Reference Diaconis and Isaacs7, Corollary 2.3] appearing in [Reference Hendrickson9] is that $\mathrm {cl}_{\mathsf {S}}(g)z=\mathrm {cl}_{\mathsf {S}}(gz)$![]() for any $z\in Z(\mathsf {S})$
for any $z\in Z(\mathsf {S})$![]() . Using this fact, as well as a consequence of [Reference Burkett3, Theorem A], we prove the following lemma that will be used in the proof of Theorem B.
. Using this fact, as well as a consequence of [Reference Burkett3, Theorem A], we prove the following lemma that will be used in the proof of Theorem B.
Lemma 3.1 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() and write $Z=Z(\mathsf {S})$
and write $Z=Z(\mathsf {S})$![]() . If $gz\notin \mathrm {cl}_{\mathsf {S}}(g)$
. If $gz\notin \mathrm {cl}_{\mathsf {S}}(g)$![]() for any $z\in Z,$
for any $z\in Z,$![]() then $\lvert {\mathrm {cl}_{\mathsf {S}_{G/Z}}(gZ)}\rvert=\lvert{\mathrm {cl}_{\mathsf {S}}(g)}\rvert$
then $\lvert {\mathrm {cl}_{\mathsf {S}_{G/Z}}(gZ)}\rvert=\lvert{\mathrm {cl}_{\mathsf {S}}(g)}\rvert$![]() .
.
Proof. Let $h\in \mathrm {cl}_{\mathsf {S}}(g)$![]() . Then $h=gg^{-1}h\in \mathrm {cl}_{\mathsf {S}}(g)$
. Then $h=gg^{-1}h\in \mathrm {cl}_{\mathsf {S}}(g)$![]() , so $g^{-1}h\notin Z$
, so $g^{-1}h\notin Z$![]() . So the map $\mathrm {cl}_{\mathsf {S}}(g)\to \mathrm {cl}_{\mathsf {S}_{G/Z}}(gZ)$
. So the map $\mathrm {cl}_{\mathsf {S}}(g)\to \mathrm {cl}_{\mathsf {S}_{G/Z}}(gZ)$![]() is injective. Since $\lvert{\mathrm {cl}_{\mathsf {S}_{G/Z}}(gZ)}\rvert$
is injective. Since $\lvert{\mathrm {cl}_{\mathsf {S}_{G/Z}}(gZ)}\rvert$![]() divides $\lvert {\mathrm {cl}_{\mathsf {S}}(g)} \rvert$
divides $\lvert {\mathrm {cl}_{\mathsf {S}}(g)} \rvert$![]() , the result follows.
, the result follows.
It turns out that many analogs of classical results about the centre of the group exist for $Z(\mathsf {S})$![]() (see [Reference Burkett3] for more details). Among these is the next result, which is a generalization of a well-known fact about ordinary complex characters (e.g., see [Reference Isaacs11, Corollary 2.30]).
(see [Reference Burkett3] for more details). Among these is the next result, which is a generalization of a well-known fact about ordinary complex characters (e.g., see [Reference Isaacs11, Corollary 2.30]).
Lemma 3.2 Let $\chi$![]() be a basic $\mathsf {S}$
be a basic $\mathsf {S}$![]() -character of $G$
-character of $G$![]() and write $Z=Z(\mathsf {S})$
and write $Z=Z(\mathsf {S})$![]() . Then $\chi (1)\le \lvert {G:Z(\mathsf {S})}\rvert,$
. Then $\chi (1)\le \lvert {G:Z(\mathsf {S})}\rvert,$![]() with equality if and only if $\chi$
with equality if and only if $\chi$![]() vanishes on $G\setminus Z(\mathsf {S})$
vanishes on $G\setminus Z(\mathsf {S})$![]() .
.
Proof. Since $\mathsf {S}_{Z(\mathsf {S})}$![]() is the finest supercharacter theory, the restriction $\chi _{Z(\mathsf {S})}$
is the finest supercharacter theory, the restriction $\chi _{Z(\mathsf {S})}$![]() is a multiple of some linear character $\lambda$
is a multiple of some linear character $\lambda$![]() . So $\langle{\chi _{Z(\mathsf {S})},\,\chi _{Z(\mathsf {S})}}\rangle=\chi (1)^{2}$
. So $\langle{\chi _{Z(\mathsf {S})},\,\chi _{Z(\mathsf {S})}}\rangle=\chi (1)^{2}$![]() . On the other hand, $\langle{\chi _{Z(\mathsf {S})},\,\chi _{Z(\mathsf {S})}}\rangle \le \lvert {G:Z(\mathsf {S})}\rvert\langle {\chi,\,\chi }\rangle=\lvert {G:Z(\mathsf {S})}\rvert\chi (1)$
. On the other hand, $\langle{\chi _{Z(\mathsf {S})},\,\chi _{Z(\mathsf {S})}}\rangle \le \lvert {G:Z(\mathsf {S})}\rvert\langle {\chi,\,\chi }\rangle=\lvert {G:Z(\mathsf {S})}\rvert\chi (1)$![]() , with equality if and only if $\chi$
, with equality if and only if $\chi$![]() vanishes on $G\setminus Z(\mathsf {S})$
vanishes on $G\setminus Z(\mathsf {S})$![]() . The result follows.
. The result follows.
We now discuss an analog of the commutator subgroup of $G$![]() . Note that one may write $[G,\,G]=\langle{g^{-1}k:k\in \mathrm {cl}_G(g)}\rangle$
. Note that one may write $[G,\,G]=\langle{g^{-1}k:k\in \mathrm {cl}_G(g)}\rangle$![]() . Using this description, it is natural to consider the subgroup $\langle{g^{-1}k:k\in \mathrm {cl}_{\mathsf {S}}(g)}\rangle$
. Using this description, it is natural to consider the subgroup $\langle{g^{-1}k:k\in \mathrm {cl}_{\mathsf {S}}(g)}\rangle$![]() , which we denote by $[G,\,\mathsf {S}]$
, which we denote by $[G,\,\mathsf {S}]$![]() . It turns out this subgroup is always $\mathsf {S}$
. It turns out this subgroup is always $\mathsf {S}$![]() -normal [Reference Burkett3, Proposition 3.7]. Moreover, $[G,\,\mathsf {S}]$
-normal [Reference Burkett3, Proposition 3.7]. Moreover, $[G,\,\mathsf {S}]$![]() provides information of the structure of the basic $\mathsf {S}$
provides information of the structure of the basic $\mathsf {S}$![]() -characters. Most notably, a basic $\mathsf {S}$
-characters. Most notably, a basic $\mathsf {S}$![]() -character $\chi$
-character $\chi$![]() is linear if and only if $[G,\,\mathsf {S}]\le \ker (\chi )$
is linear if and only if $[G,\,\mathsf {S}]\le \ker (\chi )$![]() [Reference Burkett3, Proposition 3.11].
[Reference Burkett3, Proposition 3.11].
As stated above, if $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() , $N$
, $N$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, $\chi$
-normal, $\chi$![]() is a basic $\mathsf {S}$
is a basic $\mathsf {S}$![]() -character and $\psi$
-character and $\psi$![]() is a basic $\mathsf {S}_N$
is a basic $\mathsf {S}_N$![]() -character satisfying $\langle{\chi _N,\,\psi }\rangle >0$
-character satisfying $\langle{\chi _N,\,\psi }\rangle >0$![]() , then $\psi (1)$
, then $\psi (1)$![]() divides $\chi (1)$
divides $\chi (1)$![]() . The next result, which is [Reference Burkett3, Proposition 3.13], shows this can be strengthened in certain situations, a fact that will be useful later.
. The next result, which is [Reference Burkett3, Proposition 3.13], shows this can be strengthened in certain situations, a fact that will be useful later.
Lemma 3.3 Let $N$![]() be an $\mathsf {S}$
be an $\mathsf {S}$![]() -normal subgroup satisfying $[G,\,\mathsf {S}]\le N$
-normal subgroup satisfying $[G,\,\mathsf {S}]\le N$![]() . Let $\chi$
. Let $\chi$![]() be a basic $\mathsf {S}$
be a basic $\mathsf {S}$![]() -character that does not contain $N$
-character that does not contain $N$![]() in its kernel, and suppose that $\psi \in \mathrm {BCh}(\mathsf {S}_N)$
in its kernel, and suppose that $\psi \in \mathrm {BCh}(\mathsf {S}_N)$![]() satisfies $\langle{\chi _N,\,\psi }\rangle>0$
satisfies $\langle{\chi _N,\,\psi }\rangle>0$![]() . Then $\chi (1)/\psi (1)$
. Then $\chi (1)/\psi (1)$![]() divides $\lvert {G:N}\rvert$
divides $\lvert {G:N}\rvert$![]() .
.
Proof. Since $[G,\,\mathsf {S}]\le N$![]() , $\Lambda =\mathrm {Ch}(\mathsf {S}/N)$
, $\Lambda =\mathrm {Ch}(\mathsf {S}/N)$![]() acts on $\mathrm {BCh}(\mathsf {S})$
acts on $\mathrm {BCh}(\mathsf {S})$![]() in the obvious way. Consider the set $C=\{\psi \lambda :\ \psi \in X,\,\ \lambda \in \Lambda \}$
in the obvious way. Consider the set $C=\{\psi \lambda :\ \psi \in X,\,\ \lambda \in \Lambda \}$![]() , where $X=\mathrm {Irr}(\chi )$
, where $X=\mathrm {Irr}(\chi )$![]() . On the one hand, $C$
. On the one hand, $C$![]() is exactly the set of constituents of $\psi ^{G}$
is exactly the set of constituents of $\psi ^{G}$![]() . By [Reference Hendrickson9, Lemma 3.4], we conclude that
. By [Reference Hendrickson9, Lemma 3.4], we conclude that
On the other hand, we have $C=\bigcup _{\lambda \in \Lambda }X^{\lambda }$![]() . Since $\mathrm {Irr}(\chi ^{\lambda })\cap \mathrm {Irr}(\chi )=\varnothing$
. Since $\mathrm {Irr}(\chi ^{\lambda })\cap \mathrm {Irr}(\chi )=\varnothing$![]() whenever $\chi ^{\lambda }\neq \chi$
whenever $\chi ^{\lambda }\neq \chi$![]() and $\chi ^{\lambda }(1)=\chi (1)$
and $\chi ^{\lambda }(1)=\chi (1)$![]() for each $\lambda \in \Lambda$
for each $\lambda \in \Lambda$![]() , we have
, we have
Thus, we have
The result follows as $\lvert {\mathrm {Stab}_{\Lambda }(\chi )}\rvert$![]() divides $\lvert{G:N}\rvert$
divides $\lvert{G:N}\rvert$![]() .
.
Remark 3.4 If $\chi \in \mathrm {Irr}(G)$![]() and $\psi \in \mathrm {Irr}(N)$
and $\psi \in \mathrm {Irr}(N)$![]() lie under $\chi$
lie under $\chi$![]() , then $\chi (1)/\psi (1)$
, then $\chi (1)/\psi (1)$![]() is known to divide $\lvert {G:N}\rvert$
is known to divide $\lvert {G:N}\rvert$![]() (for a proof, see [Reference Isaacs11, Corollary 11.29]). In the case $\mathsf {S}=\mathsf {m}(G)$
(for a proof, see [Reference Isaacs11, Corollary 11.29]). In the case $\mathsf {S}=\mathsf {m}(G)$![]() , Lemma 3.3 is saying something a little stronger. In this case, a basic $\mathsf {S}$
, Lemma 3.3 is saying something a little stronger. In this case, a basic $\mathsf {S}$![]() -character has the form $\chi (1)\chi$
-character has the form $\chi (1)\chi$![]() for some $\chi \in \mathrm {Irr}(G)$
for some $\chi \in \mathrm {Irr}(G)$![]() . If $\psi \in \mathrm {Irr}(N)$
. If $\psi \in \mathrm {Irr}(N)$![]() lies under $\chi$
lies under $\chi$![]() , then a basic $\mathsf {S}_N$
, then a basic $\mathsf {S}_N$![]() character has degree $\lvert {G:I_G(\psi )}\rvert$
character has degree $\lvert {G:I_G(\psi )}\rvert$![]() , where $I_G(\psi )$
, where $I_G(\psi )$![]() is the inertia group of $\psi$
is the inertia group of $\psi$![]() in $G$
in $G$![]() . Therefore, in this case, Lemma 3.3 is saying that if $G/N$
. Therefore, in this case, Lemma 3.3 is saying that if $G/N$![]() is abelian, $(\chi (1)/\psi (1))^{2}$
is abelian, $(\chi (1)/\psi (1))^{2}$![]() divides $\lvert {G:N}\rvert \lvert{G:I_G(\psi )}\rvert$
divides $\lvert {G:N}\rvert \lvert{G:I_G(\psi )}\rvert$![]() .
.
4. Proofs
In this section, we prove the main results of the paper. For the remainder of the paper, $p$![]() is an odd prime and $G$
is an odd prime and $G$![]() is the abelian group of order $p^{2}$
is the abelian group of order $p^{2}$![]() and exponent $p$
and exponent $p$![]() .
.
Our first result shows that every $\ast$![]() -product and direct product supercharacter theory of $G$
-product and direct product supercharacter theory of $G$![]() comes from automorphisms. Note that this includes Theorem A.
comes from automorphisms. Note that this includes Theorem A.
Lemma 4.1 Let $N\ne M$![]() be a non-trivial, proper subgroups of $G$
be a non-trivial, proper subgroups of $G$![]() . Let $\varphi :M\to G/N$
. Let $\varphi :M\to G/N$![]() be the canonical isomorphism $x\mapsto xN$
be the canonical isomorphism $x\mapsto xN$![]() . Let $\mathsf {U}$
. Let $\mathsf {U}$![]() be a supercharacter theory of $N,$
be a supercharacter theory of $N,$![]() and let $\mathsf {V}$
and let $\mathsf {V}$![]() be a supercharacter theory of $M$
be a supercharacter theory of $M$![]() . The following hold:
. The following hold:
(1) There exists $A\le \mathrm {Aut}(G)$
 such that $\mathsf {U}\ast \varphi (\mathsf {V})$
such that $\mathsf {U}\ast \varphi (\mathsf {V})$ comes from $A;$
comes from $A;$
(2) There exists $B\le \mathrm {Aut}(G)$
 such that $\mathsf {U}\times \mathsf {V}$
such that $\mathsf {U}\times \mathsf {V}$ comes from $B$
comes from $B$ .
.
Proof. Write $N=\langle{x}\rangle$![]() and $M=\langle{y}\rangle$
and $M=\langle{y}\rangle$![]() . Since $N$
. Since $N$![]() and $M$
and $M$![]() are cyclic of prime order, there exist integers $m_1$
are cyclic of prime order, there exist integers $m_1$![]() , $m_2$
, $m_2$![]() such that $\mathsf {U}$
such that $\mathsf {U}$![]() comes from the automorphism $\sigma :N\to N$
comes from the automorphism $\sigma :N\to N$![]() defined by $x^{\sigma }=x^{m_1}$
defined by $x^{\sigma }=x^{m_1}$![]() and $\mathsf {U}$
and $\mathsf {U}$![]() comes from the automorphism $\tau :M\to M$
comes from the automorphism $\tau :M\to M$![]() defined by $y^{\tau }=y^{m_2}$
defined by $y^{\tau }=y^{m_2}$![]() .
.
First, we prove (1). Let $\mathsf {S}=\mathsf {U}\ast \varphi (\mathsf {V})$![]() . Then the $\mathsf {S}$
. Then the $\mathsf {S}$![]() -classes contained in $N$
-classes contained in $N$![]() are the orbits of $\langle{\sigma }\rangle$
are the orbits of $\langle{\sigma }\rangle$![]() on $N$
on $N$![]() . The $\mathsf {S}$
. The $\mathsf {S}$![]() -classes lying outside of $N$
-classes lying outside of $N$![]() are the full preimages of the orbits of $\langle{\tau }\rangle$
are the full preimages of the orbits of $\langle{\tau }\rangle$![]() on $M$
on $M$![]() under the projection $G\to G/N$
under the projection $G\to G/N$![]() . Extend $\sigma$
. Extend $\sigma$![]() to an automorphism $\tilde {\sigma }$
to an automorphism $\tilde {\sigma }$![]() of $G$
of $G$![]() by setting $y^{\tilde {\sigma }}=y$
by setting $y^{\tilde {\sigma }}=y$![]() . For each $1\le k\le p-1$
. For each $1\le k\le p-1$![]() , define the automorphism $\tau _k$
, define the automorphism $\tau _k$![]() of $G$
of $G$![]() by defining $(x^{i}y^{j})^{\tau _k}=x^{i+jk}y^{jm_2}$
by defining $(x^{i}y^{j})^{\tau _k}=x^{i+jk}y^{jm_2}$![]() . Let $A=\langle{\tilde {\sigma },\,\tau _1,\,\tau _2,\,\dotsc,\,\tau _{p-1}}\rangle$
. Let $A=\langle{\tilde {\sigma },\,\tau _1,\,\tau _2,\,\dotsc,\,\tau _{p-1}}\rangle$![]() . Then $N$
. Then $N$![]() is $A$
is $A$![]() -invariant and the orbits of $A$
-invariant and the orbits of $A$![]() on $N$
on $N$![]() are exactly the orbits of $\langle{\sigma }\rangle$
are exactly the orbits of $\langle{\sigma }\rangle$![]() on $N$
on $N$![]() . Thus, $\mathrm {orb}_A(g)=\mathrm {cl}_{\mathsf {S}}(g)$
. Thus, $\mathrm {orb}_A(g)=\mathrm {cl}_{\mathsf {S}}(g)$![]() if $g\in N$
if $g\in N$![]() . Observe that $\{1,\,y,\,\dotsc,\,y^{p-1}\}$
. Observe that $\{1,\,y,\,\dotsc,\,y^{p-1}\}$![]() is a transversal for $N$
is a transversal for $N$![]() in $G$
in $G$![]() . For each $1\le j,\,k\le p-1$
. For each $1\le j,\,k\le p-1$![]() , observe that $(y^{j})^{\tau _k}=y^{jm_2}x^{jk}$
, observe that $(y^{j})^{\tau _k}=y^{jm_2}x^{jk}$![]() . As $k$
. As $k$![]() ranges over the set $\{1,\,2,\,\dotsc,\,p-1\}$
ranges over the set $\{1,\,2,\,\dotsc,\,p-1\}$![]() , so does $jk$
, so does $jk$![]() . It follows that $\mathrm {orb}_A(y^{j})=\{hn:h\in \mathrm {orb}_{\langle{\tau }\rangle}(y^{j}),\, n\in N\}$
. It follows that $\mathrm {orb}_A(y^{j})=\{hn:h\in \mathrm {orb}_{\langle{\tau }\rangle}(y^{j}),\, n\in N\}$![]() . For each $g\in G$
. For each $g\in G$![]() , we may write $g$
, we may write $g$![]() uniquely as $g=g_Ng_M$
uniquely as $g=g_Ng_M$![]() where $g_N\in N$
where $g_N\in N$![]() and $g_M$
and $g_M$![]() . Let $g\in G$
. Let $g\in G$![]() . From the arguments above, we see that $\mathrm {orb}_A(g)=\{hn:h\in \mathrm {orb}_{\langle {\tau }\rangle}(g_M),\, n\in N\}$
. From the arguments above, we see that $\mathrm {orb}_A(g)=\{hn:h\in \mathrm {orb}_{\langle {\tau }\rangle}(g_M),\, n\in N\}$![]() , which is exactly $\mathrm {cl}_{\mathsf {S}}(g)$
, which is exactly $\mathrm {cl}_{\mathsf {S}}(g)$![]() . This completes the proof of (1).
. This completes the proof of (1).
Now we show (2). Let $\mathsf {D}=\mathsf {U}\times \mathsf {V}$![]() . Extend $\sigma$
. Extend $\sigma$![]() to an automorphism $\tilde {\sigma }$
to an automorphism $\tilde {\sigma }$![]() of $G$
of $G$![]() by setting $y^{\tilde {\sigma }}=y$
by setting $y^{\tilde {\sigma }}=y$![]() , and extend $\tau$
, and extend $\tau$![]() to an automorphism $\tilde {\tau }$
to an automorphism $\tilde {\tau }$![]() of $G$
of $G$![]() by setting $x^{\tilde {\tau }}=x$
by setting $x^{\tilde {\tau }}=x$![]() . Let $B=\langle {\tilde {\sigma },\,\tilde {\tau }}\rangle$
. Let $B=\langle {\tilde {\sigma },\,\tilde {\tau }}\rangle$![]() . Then $N$
. Then $N$![]() and $M$
and $M$![]() are both $B$
are both $B$![]() -invariant. If $g\in N\cup M$
-invariant. If $g\in N\cup M$![]() , then it is easy to see that $\mathrm {orb}_B(g)=\mathrm {cl}_{\mathsf {D}}(g)$
, then it is easy to see that $\mathrm {orb}_B(g)=\mathrm {cl}_{\mathsf {D}}(g)$![]() . If $g\not \in N\cup M$
. If $g\not \in N\cup M$![]() , then
, then

where $d_i$![]() is the order of $m_i$
is the order of $m_i$![]() modulo $p$
modulo $p$![]() . Thus, $\mathrm {orb}_B(g)=\mathrm {orb}_{\langle{\sigma }\rangle}(g_N)\times \mathrm {orb}_{\langle{\tau }\rangle}(g_M)=\mathrm {cl}_{\mathsf {S}}(g)$
. Thus, $\mathrm {orb}_B(g)=\mathrm {orb}_{\langle{\sigma }\rangle}(g_N)\times \mathrm {orb}_{\langle{\tau }\rangle}(g_M)=\mathrm {cl}_{\mathsf {S}}(g)$![]() . This completes the proof of (2).
. This completes the proof of (2).
We may now give a more precise statement and proof of Theorem B. We first remark that having a non-identity superclass of size $1$![]() is equivalent to the condition $Z(\mathsf {S}) > 1$
is equivalent to the condition $Z(\mathsf {S}) > 1$![]() and having a non-principal linear supercharacter is equivalent to the condition $[G,\,\mathsf {S}] < G$
and having a non-principal linear supercharacter is equivalent to the condition $[G,\,\mathsf {S}] < G$![]() .
.
Theorem 4.2 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() . Assume that $[G,\,\mathsf {S}]< G$
. Assume that $[G,\,\mathsf {S}]< G$![]() or $Z(\mathsf {S})>1$
or $Z(\mathsf {S})>1$![]() . One of the following holds:
. One of the following holds:
(1) $\mathsf {S}$
 is a $\ast$
is a $\ast$ -product over $[G,\,\mathsf {S}]$
-product over $[G,\,\mathsf {S}]$ .
.(2) $\mathsf {S}$
 is a $\ast$
is a $\ast$ -product over $Z(\mathsf {S})$
-product over $Z(\mathsf {S})$ .
.(3) $\mathsf {S}$
 is a direct product over $[G,\,\mathsf {S}]$
is a direct product over $[G,\,\mathsf {S}]$ and $Z(\mathsf {S})$
and $Z(\mathsf {S})$ .
.
In particular, $\mathsf {S}$![]() comes from automorphisms.
comes from automorphisms.
Proof. First observe that $[G,\,\mathsf {S}]=1$![]() if and only if $Z(\mathsf {S})=G$
if and only if $Z(\mathsf {S})=G$![]() , and the result holds trivially in this case. Thus, it suffices to assume that $[G,\,\mathsf {S}]$
, and the result holds trivially in this case. Thus, it suffices to assume that $[G,\,\mathsf {S}]$![]() or $Z(\mathsf {S})$
or $Z(\mathsf {S})$![]() is non-trivial and proper. We can make another reduction by considering $G^{\ast }=\mathrm {Irr}(G)$
is non-trivial and proper. We can make another reduction by considering $G^{\ast }=\mathrm {Irr}(G)$![]() – the dual of $G$
– the dual of $G$![]() – and the dual supercharacter theory ${\check {S}}$
– and the dual supercharacter theory ${\check {S}}$![]() of $\mathsf {S}$
of $\mathsf {S}$![]() . If $\mathsf {S}=(\mathcal {X},\,\mathcal {K})$
. If $\mathsf {S}=(\mathcal {X},\,\mathcal {K})$![]() , then $Z(\mathsf {S})$
, then $Z(\mathsf {S})$![]() and $\mathrm {BCh}(G/[G,\,\mathsf {S}])$
and $\mathrm {BCh}(G/[G,\,\mathsf {S}])$![]() are comprised of the parts of $\mathcal {K}$
are comprised of the parts of $\mathcal {K}$![]() and $\mathcal {X}$
and $\mathcal {X}$![]() of size 1, respectively. From this description, it is clear that $Z(\mathsf {S})^{\ast }=G^{\ast }/[G^{\ast },\,{\check {S}}]$
of size 1, respectively. From this description, it is clear that $Z(\mathsf {S})^{\ast }=G^{\ast }/[G^{\ast },\,{\check {S}}]$![]() and $Z({\check {\mathsf {S}}})=(G/[G,\,\mathsf {S}])^{\ast }$
and $Z({\check {\mathsf {S}}})=(G/[G,\,\mathsf {S}])^{\ast }$![]() . Thus, it suffices to prove that the result holds in the case that $1<[G,\,\mathsf {S}]< G$
. Thus, it suffices to prove that the result holds in the case that $1<[G,\,\mathsf {S}]< G$![]() , which we now assume.
, which we now assume.
We first assume additionally that $[G,\,\mathsf {S}]$![]() is the unique $\mathsf {S}$
is the unique $\mathsf {S}$![]() -normal subgroup of index $p$
-normal subgroup of index $p$![]() . Then either ${Z}(\mathsf {S})=1$
. Then either ${Z}(\mathsf {S})=1$![]() or ${Z}(\mathsf {S})=[G,\,\mathsf {S}]$
or ${Z}(\mathsf {S})=[G,\,\mathsf {S}]$![]() . Assume that ${Z}(\mathsf {S})=[G,\,\mathsf {S}]$
. Assume that ${Z}(\mathsf {S})=[G,\,\mathsf {S}]$![]() . Let $\chi$
. Let $\chi$![]() be an $\mathsf {S}$
be an $\mathsf {S}$![]() -character without $[G,\,\mathsf {S}]$
-character without $[G,\,\mathsf {S}]$![]() in its kernel. Then $\chi (1)=\lvert {G:{Z}(\mathsf {S})}\rvert=p$
in its kernel. Then $\chi (1)=\lvert {G:{Z}(\mathsf {S})}\rvert=p$![]() . By Lemma 3.2, we deduce that $\chi$
. By Lemma 3.2, we deduce that $\chi$![]() vanishes on $G\setminus {Z}(\mathsf {S})$
vanishes on $G\setminus {Z}(\mathsf {S})$![]() . Hence we see from [Reference Burkett and Lewis5, Theorem 2] that $\mathsf {S}$
. Hence we see from [Reference Burkett and Lewis5, Theorem 2] that $\mathsf {S}$![]() is a $\ast$
is a $\ast$![]() -product over $[G,\,\mathsf {S}]$
-product over $[G,\,\mathsf {S}]$![]() . So we now assume that ${Z}(\mathsf {S})=1$
. So we now assume that ${Z}(\mathsf {S})=1$![]() . Let $\chi \in \mathrm {BCh}(\mathsf {S}\mid [G,\,\mathsf {S}])$
. Let $\chi \in \mathrm {BCh}(\mathsf {S}\mid [G,\,\mathsf {S}])$![]() , and let $\psi \in \mathrm {BCh}([G,\,\mathsf {S}])$
, and let $\psi \in \mathrm {BCh}([G,\,\mathsf {S}])$![]() lie under $\chi$
lie under $\chi$![]() . If every element of $\mathrm {Irr}(G/[G,\,\mathsf {S}])$
. If every element of $\mathrm {Irr}(G/[G,\,\mathsf {S}])$![]() fixes $\chi$
fixes $\chi$![]() , then $\chi$
, then $\chi$![]() vanishes on $G\setminus [G,\,\mathsf {S}]$
vanishes on $G\setminus [G,\,\mathsf {S}]$![]() and so $\chi =\psi ^{G}$
and so $\chi =\psi ^{G}$![]() by Lemma 2.1. Let $1\le j\le p-1$
by Lemma 2.1. Let $1\le j\le p-1$![]() . Then $\chi ^{j}\in \mathrm {BCh}(\mathsf {S})$
. Then $\chi ^{j}\in \mathrm {BCh}(\mathsf {S})$![]() and $\chi ^{j}=(\psi ^{j})^{G}$
and $\chi ^{j}=(\psi ^{j})^{G}$![]() , where here $\alpha ^{j}(g)=\alpha (g^{j})$
, where here $\alpha ^{j}(g)=\alpha (g^{j})$![]() . As $j$
. As $j$![]() ranges over all $j$
ranges over all $j$![]() , $\psi ^{j}$
, $\psi ^{j}$![]() ranges over all non-principal basic $\mathsf {S}_{[G,\mathsf {S}]}$
ranges over all non-principal basic $\mathsf {S}_{[G,\mathsf {S}]}$![]() -characters. Thus, we see that every $\chi \in \mathrm {BCh}(\mathsf {S}\mid [G,\,\mathsf {S}])$
-characters. Thus, we see that every $\chi \in \mathrm {BCh}(\mathsf {S}\mid [G,\,\mathsf {S}])$![]() vanishes on $G\setminus [G,\,\mathsf {S}]$
vanishes on $G\setminus [G,\,\mathsf {S}]$![]() . Hence $\mathsf {S}$
. Hence $\mathsf {S}$![]() is a $\ast$
is a $\ast$![]() -product over $[G,\,\mathsf {S}]$
-product over $[G,\,\mathsf {S}]$![]() in this case as well. So assume that this is not the case. We instead consider the dual situation in $G^{\ast }=\mathrm {Irr}(G)$
in this case as well. So assume that this is not the case. We instead consider the dual situation in $G^{\ast }=\mathrm {Irr}(G)$![]() . Then $Z={Z}({\check {\mathsf {S}}})$
. Then $Z={Z}({\check {\mathsf {S}}})$![]() has order $p$
has order $p$![]() , $[G^{\ast },\,{\check {\mathsf {S}}}]=G^{\ast }$
, $[G^{\ast },\,{\check {\mathsf {S}}}]=G^{\ast }$![]() and that $\mathrm {cl}_{\check {\mathsf {S}}}(g)$
and that $\mathrm {cl}_{\check {\mathsf {S}}}(g)$![]() is not fixed by the action of $Z$
is not fixed by the action of $Z$![]() for any $g\in G^{\ast }\setminus Z$
for any $g\in G^{\ast }\setminus Z$![]() . Let $h\in G^{\ast }\setminus Z$
. Let $h\in G^{\ast }\setminus Z$![]() . Then $\langle{h}\rangle$
. Then $\langle{h}\rangle$![]() gives a transversal for $Z$
gives a transversal for $Z$![]() in $G^{\ast }$
in $G^{\ast }$![]() . Since $G^{\ast }/Z\simeq C_p$
. Since $G^{\ast }/Z\simeq C_p$![]() , there exists $1\le m\le p-1$
, there exists $1\le m\le p-1$![]() such that $\mathrm {cl}_{ {\check {\mathsf {S}}}_{G/Z}}(hZ)=\{hZ,\,h^{m}Z,\,\dotsc,\,h^{m^{d-1}}Z\}$
such that $\mathrm {cl}_{ {\check {\mathsf {S}}}_{G/Z}}(hZ)=\{hZ,\,h^{m}Z,\,\dotsc,\,h^{m^{d-1}}Z\}$![]() , where $d=\mathrm {ord}_p(m)$
, where $d=\mathrm {ord}_p(m)$![]() . Also, since $\lvert {\mathrm {cl}_{\check {\mathsf {S}}}(h)}\rvert=\lvert {\mathrm {cl}_{\check {\mathsf {S}}_{G/Z}}(hZ)}\rvert$
. Also, since $\lvert {\mathrm {cl}_{\check {\mathsf {S}}}(h)}\rvert=\lvert {\mathrm {cl}_{\check {\mathsf {S}}_{G/Z}}(hZ)}\rvert$![]() by Lemma 3.1, there exist $z_1,\,z_2,\,\dotsc,\,z_{d-1}\in {Z}({\check {\mathsf {S}}})$
by Lemma 3.1, there exist $z_1,\,z_2,\,\dotsc,\,z_{d-1}\in {Z}({\check {\mathsf {S}}})$![]() such that $\mathrm {cl}_{\check {\mathsf {S}}}(h)=\{h,\,h^{m}z_1,\,h^{m^{2}}z_2,\,\dotsc,\,h^{m^{d-1}}z_{d-1}\}$
such that $\mathrm {cl}_{\check {\mathsf {S}}}(h)=\{h,\,h^{m}z_1,\,h^{m^{2}}z_2,\,\dotsc,\,h^{m^{d-1}}z_{d-1}\}$![]() . So
. So
from which it follows that $\mathrm {cl}_{\check {\mathsf {S}}}(h^{m})z_1=\mathrm {cl}_{\check {\mathsf {S}}}(h)$![]() . Since $\mathrm {cl}_{\check {\mathsf {S}}}(h)$
. Since $\mathrm {cl}_{\check {\mathsf {S}}}(h)$![]() is not fixed by multiplication by any element of $Z$
is not fixed by multiplication by any element of $Z$![]() , this implies that $z_2=z_1^{m+1}$
, this implies that $z_2=z_1^{m+1}$![]() . Similarly $z_3=z_2^{m}z_1=z_1^{m^{2}+m+1}$
. Similarly $z_3=z_2^{m}z_1=z_1^{m^{2}+m+1}$![]() . Continuing this way, we deduce that $z_i =z^{1+m+m^{2}+\dotsb +m^{i-1}}=z_1^{(m^{i}-1)/(m-1)}$
. Continuing this way, we deduce that $z_i =z^{1+m+m^{2}+\dotsb +m^{i-1}}=z_1^{(m^{i}-1)/(m-1)}$![]() for each $1\le i\le d-1$
for each $1\le i\le d-1$![]() , where $z=z_1$
, where $z=z_1$![]() . Thus, we see that $h^{-1}k\in \langle{h^{m-1}z}\rangle$
. Thus, we see that $h^{-1}k\in \langle{h^{m-1}z}\rangle$![]() for every $k\in \mathrm {cl}_{\check {\mathsf {S}}}(h)$
for every $k\in \mathrm {cl}_{\check {\mathsf {S}}}(h)$![]() . Similarly, for every $w\in Z$
. Similarly, for every $w\in Z$![]() and $k\in \mathrm {cl}_{\check {\mathsf {S}}}(hw)$
and $k\in \mathrm {cl}_{\check {\mathsf {S}}}(hw)$![]() , $(hw)^{-1}k\in \langle{h^{m-1}z}\rangle$
, $(hw)^{-1}k\in \langle{h^{m-1}z}\rangle$![]() . Since every element of $G^{\ast }$
. Since every element of $G^{\ast }$![]() has the form $h^{j}w$
has the form $h^{j}w$![]() for some integer $j$
for some integer $j$![]() and $w\in Z$
and $w\in Z$![]() , it follows that $g^{-1}k\in \langle {h^{m-1}z}\rangle$
, it follows that $g^{-1}k\in \langle {h^{m-1}z}\rangle$![]() for every $g\in G^{\ast }$
for every $g\in G^{\ast }$![]() and $k\in \mathrm {cl}_{\check {\mathsf {S}}}(g)$
and $k\in \mathrm {cl}_{\check {\mathsf {S}}}(g)$![]() . This implies that $[G^{\ast },\,{\check {\mathsf {S}}}]=\langle{h^{m-1}z}\rangle< G^{\ast }$
. This implies that $[G^{\ast },\,{\check {\mathsf {S}}}]=\langle{h^{m-1}z}\rangle< G^{\ast }$![]() , a contradiction.
, a contradiction.
We may now assume that there is another $\mathsf {S}$![]() -normal subgroup, say $N$
-normal subgroup, say $N$![]() . Since $[G,\,\mathsf {S}]< G$
. Since $[G,\,\mathsf {S}]< G$![]() , $[G,\,\mathsf {S}]\ne Z(\mathsf {S})$
, $[G,\,\mathsf {S}]\ne Z(\mathsf {S})$![]() . So $N\cap [G,\,\mathsf {S}]=1$
. So $N\cap [G,\,\mathsf {S}]=1$![]() , which implies $N={Z}(\mathsf {S})$
, which implies $N={Z}(\mathsf {S})$![]() . Let $\chi \in \mathrm {BCh}(\mathsf {S})$
. Let $\chi \in \mathrm {BCh}(\mathsf {S})$![]() satisfy $[G,\,\mathsf {S}]\nleq \ker (\chi )$
satisfy $[G,\,\mathsf {S}]\nleq \ker (\chi )$![]() . Let $\psi \in \mathrm {BCh}(\mathsf {S}_{[G,\mathsf {S}]})$
. Let $\psi \in \mathrm {BCh}(\mathsf {S}_{[G,\mathsf {S}]})$![]() lie under $\chi$
lie under $\chi$![]() . Then $\chi (1)/\psi (1)\in \{1,\,p\}$
. Then $\chi (1)/\psi (1)\in \{1,\,p\}$![]() by Lemma 3.3. Assume that $\chi (1)=p\psi (1)$
by Lemma 3.3. Assume that $\chi (1)=p\psi (1)$![]() . Since $\chi (1)\le \lvert {G:Z(\mathsf {S})}\rvert = p$
. Since $\chi (1)\le \lvert {G:Z(\mathsf {S})}\rvert = p$![]() by Lemma 3.2, we deduce that $\psi (1)=1$
by Lemma 3.2, we deduce that $\psi (1)=1$![]() . Since $[G,\,\mathsf {S}]\nleq \ker (\chi )$
. Since $[G,\,\mathsf {S}]\nleq \ker (\chi )$![]() , $\psi$
, $\psi$![]() is non-principal and thus $[[G,\,\mathsf {S}],\,\mathsf {S}]=1$
is non-principal and thus $[[G,\,\mathsf {S}],\,\mathsf {S}]=1$![]() . We conclude that $\mathsf {S}_{[G,\mathsf {S}]}=\mathsf {m}([G,\,\mathsf {S}])$
. We conclude that $\mathsf {S}_{[G,\mathsf {S}]}=\mathsf {m}([G,\,\mathsf {S}])$![]() , which contradicts the fact that $[G,\,\mathsf {S}]\ne Z(\mathsf {S})$
, which contradicts the fact that $[G,\,\mathsf {S}]\ne Z(\mathsf {S})$![]() . So $\chi (1)=\psi (1)$
. So $\chi (1)=\psi (1)$![]() and so $\psi ^{G}$
and so $\psi ^{G}$![]() is the sum of $p$
is the sum of $p$![]() distinct $\mathsf {S}$
distinct $\mathsf {S}$![]() -characters. If $\mathrm {BCh}(\mathsf {S}/[G,\,\mathsf {S}])$
-characters. If $\mathrm {BCh}(\mathsf {S}/[G,\,\mathsf {S}])$![]() is the set of basic $\mathsf {S}$
is the set of basic $\mathsf {S}$![]() -characters with $[G,\,\mathsf {S}]$
-characters with $[G,\,\mathsf {S}]$![]() in their kernel and $\mathrm {BCh}(\mathsf {S}\mid [G,\,\mathsf {S}])$
in their kernel and $\mathrm {BCh}(\mathsf {S}\mid [G,\,\mathsf {S}])$![]() is the set of those without $[G,\,\mathsf {S}]$
is the set of those without $[G,\,\mathsf {S}]$![]() in their kernel, then by the above argument we see
in their kernel, then by the above argument we see

It follows from Corollary 2.3 that $\mathsf {S}=\mathsf {S}_{{Z}(\mathsf {S})}\times \mathsf {S}_{[G,\mathsf {S}]}$![]() .
.
The final statement is a consequence of Lemma 4.1
5. Partition supercharacter theories
We now describe a type of supercharacter theory that is (essentially) unique to elementary abelian groups of rank two. As in the previous section, $p$![]() is a prime and $G$
is a prime and $G$![]() is the elementary abelian group $C_p\times C_p$
is the elementary abelian group $C_p\times C_p$![]() .
.
Lemma 5.1 Let $G$![]() and let $H_1,\,H_2,\,\dotsc,\,H_{p+1}$
and let $H_1,\,H_2,\,\dotsc,\,H_{p+1}$![]() be the non-trivial, proper subgroups of $G$
be the non-trivial, proper subgroups of $G$![]() . For every subset $I\subseteq \{1,\,2,\,\dotsc,\,p+1\}$
. For every subset $I\subseteq \{1,\,2,\,\dotsc,\,p+1\}$![]() , define $N_I=\bigcup _{i\in I}(H_i\setminus 1)$
, define $N_I=\bigcup _{i\in I}(H_i\setminus 1)$![]() . For every partition $\mathcal {P}$
. For every partition $\mathcal {P}$![]() of $\{1,\,2,\,\dotsc,\,p+1\},$
of $\{1,\,2,\,\dotsc,\,p+1\},$![]() the partition $\{N_I:I\in \mathcal {P}\}$
the partition $\{N_I:I\in \mathcal {P}\}$![]() of $G\setminus 1$
of $G\setminus 1$![]() gives the non-identity superclasses for a supercharacter theory $\mathsf {S}_{\mathcal {P}}$
gives the non-identity superclasses for a supercharacter theory $\mathsf {S}_{\mathcal {P}}$![]() of $G$
of $G$![]() .
.
Proof. To prove this, it suffices to show that there exist non-negative integers $a_{I,J,1}$![]() and $a_{I,J,L}$
and $a_{I,J,L}$![]() such that
such that
for every $I,\,J\in \mathcal {P}$![]() . To that end, let $I,\,J\in \mathcal {P}$
. To that end, let $I,\,J\in \mathcal {P}$![]() . Then
. Then

as required.
We will call the supercharacter theory of Lemma 5.1 the partition supercharacter theory of $G$![]() corresponding to $\mathcal {P}$
corresponding to $\mathcal {P}$![]() . As can be seen from the above proof, the reason that this construction works because any two distinct normal subgroups generate $G$
. As can be seen from the above proof, the reason that this construction works because any two distinct normal subgroups generate $G$![]() . As such, the same construction will work if $G$
. As such, the same construction will work if $G$![]() is a direct product of two simple groups. That is, if $G=H_1\times H_2$
is a direct product of two simple groups. That is, if $G=H_1\times H_2$![]() , where $H_1\cong H_2$
, where $H_1\cong H_2$![]() is a simple group, then the set of non-trivial normal subgroups of $G$
is a simple group, then the set of non-trivial normal subgroups of $G$![]() is $\{H_1,\,H_2\}$
is $\{H_1,\,H_2\}$![]() . The only partitions of $\{1,\,2\}$
. The only partitions of $\{1,\,2\}$![]() are $\{1,\,2\}$
are $\{1,\,2\}$![]() , which corresponds to $\mathrm {M}(G)$
, which corresponds to $\mathrm {M}(G)$![]() , and $\{\{1\},\,\{2\}\}$
, and $\{\{1\},\,\{2\}\}$![]() , which corresponds to $\mathrm {M}(H_1)\times \mathrm {M}(H_2)$
, which corresponds to $\mathrm {M}(H_1)\times \mathrm {M}(H_2)$![]() .
.
However, if $G$![]() has at least three non-trivial normal subgroups, it is not difficult to see that $G$
has at least three non-trivial normal subgroups, it is not difficult to see that $G$![]() must be an elementary abelian group of rank two if any two distinct normal subgroups generate $G$
must be an elementary abelian group of rank two if any two distinct normal subgroups generate $G$![]() . Indeed, this condition on $G$
. Indeed, this condition on $G$![]() implies that any non-trivial, proper normal subgroup is minimal normal. Let $L,\,N,\,M$
implies that any non-trivial, proper normal subgroup is minimal normal. Let $L,\,N,\,M$![]() be distinct non-trivial, proper normal subgroups of $G$
be distinct non-trivial, proper normal subgroups of $G$![]() . Then $G=L\times N=L\times M=N\times M$
. Then $G=L\times N=L\times M=N\times M$![]() , so $G=NM\le C_G(L)$
, so $G=NM\le C_G(L)$![]() and $G=LM\le C_G(N)$
and $G=LM\le C_G(N)$![]() . Thus, we see that $G$
. Thus, we see that $G$![]() is abelian. So $L,\,N,\,M$
is abelian. So $L,\,N,\,M$![]() are cyclic of prime order. Since $L\cong G/N\cong M\cong G/L\cong N$
are cyclic of prime order. Since $L\cong G/N\cong M\cong G/L\cong N$![]() , $G=C_p\times C_p$
, $G=C_p\times C_p$![]() for some prime $p$
for some prime $p$![]() .
.
Lemma 5.2 Let $\mathcal {P}$![]() be the partition of $\{1,\,2,\,\dotsc,\,p+1\}$
be the partition of $\{1,\,2,\,\dotsc,\,p+1\}$![]() consisting of all singletons. A supercharacter theory $\mathsf {S}$
consisting of all singletons. A supercharacter theory $\mathsf {S}$![]() is a partition supercharacter theory if and only if $\mathsf {S}_{\mathcal {P}}\preccurlyeq \mathsf {S}$
is a partition supercharacter theory if and only if $\mathsf {S}_{\mathcal {P}}\preccurlyeq \mathsf {S}$![]() . In particular, the set of partition supercharacter theories is an interval in the lattice of supercharacter theories.
. In particular, the set of partition supercharacter theories is an interval in the lattice of supercharacter theories.
Proof. The supercharacter theory $\mathsf {S}$![]() is a partition supercharacter theory if and only if $\langle{g}\rangle \setminus \{1\}\subseteq \mathrm {cl}_{\mathsf {S}}(g)$
is a partition supercharacter theory if and only if $\langle{g}\rangle \setminus \{1\}\subseteq \mathrm {cl}_{\mathsf {S}}(g)$![]() holds for every $g\in G$
holds for every $g\in G$![]() . In other words, if and only if $g^{i}\in \mathrm {cl}_{\mathsf {S}}(g)$
. In other words, if and only if $g^{i}\in \mathrm {cl}_{\mathsf {S}}(g)$![]() holds for every $g\in G$
holds for every $g\in G$![]() and $1\le i\le p-1$
and $1\le i\le p-1$![]() . This is exactly the condition $\mathsf {S}_{\mathcal {P}}\preccurlyeq \mathsf {S}$
. This is exactly the condition $\mathsf {S}_{\mathcal {P}}\preccurlyeq \mathsf {S}$![]() . Thus, the interval $[\mathsf {S}_{\mathcal {P}},\,\mathsf {M}(G)]$
. Thus, the interval $[\mathsf {S}_{\mathcal {P}},\,\mathsf {M}(G)]$![]() is the set of partition supercharacter theories of $G$
is the set of partition supercharacter theories of $G$![]() .
.
Next, we give an example that shows the set of automorphic supercharacter theories is not a semilattice of $\mathrm {SCT}(G)$![]() .
.
Example 5.3 Let $p\ge 5$![]() . Let $H_1,\,H_2,\,H_3$
. Let $H_1,\,H_2,\,H_3$![]() be distinct subgroups of $G$
be distinct subgroups of $G$![]() of order $p$
of order $p$![]() . Define the supercharacter theories $\mathsf {S}$
. Define the supercharacter theories $\mathsf {S}$![]() and $\mathsf {T}$
and $\mathsf {T}$![]() as follows: $\mathsf {S}=\mathsf {M}(H_1)\times \mathsf {M}(H_2)$
as follows: $\mathsf {S}=\mathsf {M}(H_1)\times \mathsf {M}(H_2)$![]() , $\mathsf {T}=\mathsf {M}(H_2)\times \mathsf {M}(H_3)$
, $\mathsf {T}=\mathsf {M}(H_2)\times \mathsf {M}(H_3)$![]() , which are both partition supercharacter theories. So $\mathsf {S}\wedge \mathsf {T}$
, which are both partition supercharacter theories. So $\mathsf {S}\wedge \mathsf {T}$![]() is also a partition supercharacter theory by Lemma 5.2. It is not difficult to see that $H_1,\,H_2,\,H_3$
is also a partition supercharacter theory by Lemma 5.2. It is not difficult to see that $H_1,\,H_2,\,H_3$![]() are the only non-trivial, proper $(\mathsf {S}\wedge \mathsf {T})$
are the only non-trivial, proper $(\mathsf {S}\wedge \mathsf {T})$![]() -normal subgroups of $G$
-normal subgroups of $G$![]() . By Theorem A, both $\mathsf {S}$
. By Theorem A, both $\mathsf {S}$![]() and $\mathsf {T}$
and $\mathsf {T}$![]() come from automorphisms. However, $\mathsf {S}\wedge \mathsf {T}$
come from automorphisms. However, $\mathsf {S}\wedge \mathsf {T}$![]() does not come from automorphisms, since $\mathsf {S}\wedge \mathsf {T}$
does not come from automorphisms, since $\mathsf {S}\wedge \mathsf {T}$![]() has exactly three non-trivial, proper supernormal subgroups (see Lemma 6.6).
has exactly three non-trivial, proper supernormal subgroups (see Lemma 6.6).
We close this section by noting that the construction found in this section is closely related to the amorphic association schemes studied in [Reference van Dam and Muzychuk22].
6. Non-trivial $\mathsf {S}$ -normal subgroups
-normal subgroups
In this section, we discuss the structure of the supercharacter theories of $G=C_p\times C_p$![]() , $p$
, $p$![]() a prime, that have non-trivial, proper supernormal subgroups. We begin by studying the structure of supercharacter theories with exactly one such subgroup.
a prime, that have non-trivial, proper supernormal subgroups. We begin by studying the structure of supercharacter theories with exactly one such subgroup.
To prove Theorem 4.2, we showed that if $[G,\,\mathsf {S}]$![]() or $Z(\mathsf {S})$
or $Z(\mathsf {S})$![]() were the unique $\mathsf {S}$
were the unique $\mathsf {S}$![]() -normal subgroup of $G$
-normal subgroup of $G$![]() , then $\mathsf {S}$
, then $\mathsf {S}$![]() is a $\ast$
is a $\ast$![]() -product. One may wonder if a similar result holds for any supercharacter theory of $G$
-product. One may wonder if a similar result holds for any supercharacter theory of $G$![]() with a unique $\mathsf {S}$
with a unique $\mathsf {S}$![]() -normal subgroup. This is not the case, as the next example illustrates.
-normal subgroup. This is not the case, as the next example illustrates.
Example 6.1 We show that not every supercharacter theory of $C_p\times C_p$![]() with a unique non-trivial, proper supernormal subgroup is a $\ast$
with a unique non-trivial, proper supernormal subgroup is a $\ast$![]() -product. This example comes from $G=C_5\times C_5$
-product. This example comes from $G=C_5\times C_5$![]() . Write $G=\langle {x,\,y}\rangle$
. Write $G=\langle {x,\,y}\rangle$![]() . Let
. Let

One may readily verify that $K$![]() gives the set of $\mathsf {S}$
gives the set of $\mathsf {S}$![]() -classes for a supercharacter theory $\mathsf {S}$
-classes for a supercharacter theory $\mathsf {S}$![]() of $G$
of $G$![]() . Observe that $N=\langle{y}\rangle$
. Observe that $N=\langle{y}\rangle$![]() is the unique non-trivial, proper $\mathsf {S}$
is the unique non-trivial, proper $\mathsf {S}$![]() -normal subgroup. However, $\mathsf {S}$
-normal subgroup. However, $\mathsf {S}$![]() is not a $\ast$
is not a $\ast$![]() -product over $N$
-product over $N$![]() since, for example, $x$
since, for example, $x$![]() and $xy$
and $xy$![]() lie in different $\mathsf {S}$
lie in different $\mathsf {S}$![]() -classes.
-classes.
Observe that the above supercharacter theory is an example of a partition supercharacter theory. Indeed, the supercharacter theories $\mathsf {S}$![]() with a unique non-trivial, proper $\mathsf {S}$
with a unique non-trivial, proper $\mathsf {S}$![]() -normal subgroup that we have observed is either a $\ast$
-normal subgroup that we have observed is either a $\ast$![]() -product or a partition supercharacter theory. In particular, each supercharacter theory of this form has come from automorphisms or has been a partition supercharacter theory.
-product or a partition supercharacter theory. In particular, each supercharacter theory of this form has come from automorphisms or has been a partition supercharacter theory.
We have observed a similar phenomenon for those with exactly two non-trivial, proper $\mathsf {S}$![]() -normal subgroups. Specifically, it appears as though every supercharacter theory of $G$
-normal subgroups. Specifically, it appears as though every supercharacter theory of $G$![]() with exactly two non-trivial, proper supernormal subgroups either comes from automorphisms or is a partition supercharacter theory. It is, however, not the case that each such supercharacter theory that is not a partition supercharacter theory is a direct product, as can be seen from the next example.
with exactly two non-trivial, proper supernormal subgroups either comes from automorphisms or is a partition supercharacter theory. It is, however, not the case that each such supercharacter theory that is not a partition supercharacter theory is a direct product, as can be seen from the next example.
Example 6.2 Let $G=C_5\times C_5$![]() . Let $x$
. Let $x$![]() and $y$
and $y$![]() be distinct non-identity elements of $G$
be distinct non-identity elements of $G$![]() . Let $H=\langle{x}\rangle$
. Let $H=\langle{x}\rangle$![]() and $N=\langle{y}\rangle$
and $N=\langle{y}\rangle$![]() . Let $\sigma$
. Let $\sigma$![]() be the automorphism of $G$
be the automorphism of $G$![]() defined by $\sigma (x^{i}y^{j})=x^{-i}y^{2j}$
defined by $\sigma (x^{i}y^{j})=x^{-i}y^{2j}$![]() . Then the orbit of every element lying outside of $H$
. Then the orbit of every element lying outside of $H$![]() has size four, and the orbit of every non-identity element of $H$
has size four, and the orbit of every non-identity element of $H$![]() has size two. Let $\mathsf {S}$
has size two. Let $\mathsf {S}$![]() be the supercharacter theory of $G$
be the supercharacter theory of $G$![]() coming from $\langle{\sigma }\rangle$
coming from $\langle{\sigma }\rangle$![]() . Then $H$
. Then $H$![]() and $N$
and $N$![]() are the only non-trivial, proper $\mathsf {S}$
are the only non-trivial, proper $\mathsf {S}$![]() -normal subgroups of $G$
-normal subgroups of $G$![]() , $\lvert {\mathsf {S}_H}\rvert=3$
, $\lvert {\mathsf {S}_H}\rvert=3$![]() , $\lvert {\mathsf {S}_N}\rvert=2$
, $\lvert {\mathsf {S}_N}\rvert=2$![]() . Since $\lvert {\mathsf {S}_H\times \mathsf {S}_N}\rvert =\lvert {\mathsf {S}_H}\rvert \cdot \lvert {\mathsf {S}_N}\rvert =6<8=\lvert {\mathsf {S}}\rvert$
. Since $\lvert {\mathsf {S}_H\times \mathsf {S}_N}\rvert =\lvert {\mathsf {S}_H}\rvert \cdot \lvert {\mathsf {S}_N}\rvert =6<8=\lvert {\mathsf {S}}\rvert$![]() , $\mathsf {S}$
, $\mathsf {S}$![]() is not a direct product by Corollary 2.3.
is not a direct product by Corollary 2.3.
As mentioned just prior to Example 6.2, it appears as though every supercharacter theory of $G$![]() with exactly two non-trivial, proper supernormal subgroups either comes from automorphisms or is a partition supercharacter theory (in fact, we have yet to find any supercharacter theory of $C_p\times C_p$
with exactly two non-trivial, proper supernormal subgroups either comes from automorphisms or is a partition supercharacter theory (in fact, we have yet to find any supercharacter theory of $C_p\times C_p$![]() that does not either come from automorphisms or partitions). We do have some evidence of this, but only have one weak result in this direction. Before giving the result, we set up some convenient notation that will be used for the remainder of the paper.
that does not either come from automorphisms or partitions). We do have some evidence of this, but only have one weak result in this direction. Before giving the result, we set up some convenient notation that will be used for the remainder of the paper.
Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() and let $H$
and let $H$![]() be a non-trivial, proper $\mathsf {S}$
be a non-trivial, proper $\mathsf {S}$![]() -normal subgroup. Then $H$
-normal subgroup. Then $H$![]() is cyclic of prime order, so $\mathsf {S}_H$
is cyclic of prime order, so $\mathsf {S}_H$![]() comes from automorphisms, say from the subgroup $A\le \mathrm {Aut}(H)$
comes from automorphisms, say from the subgroup $A\le \mathrm {Aut}(H)$![]() . Since $\mathrm {Aut}(H)\cong C_{p-1}$
. Since $\mathrm {Aut}(H)\cong C_{p-1}$![]() is just the collection of power maps, there exists an integer $m$
is just the collection of power maps, there exists an integer $m$![]() such that $A$
such that $A$![]() is generated by the automorphism sending an element to its $m^{\rm th}$
is generated by the automorphism sending an element to its $m^{\rm th}$![]() -power. Thus, if $g\in H$
-power. Thus, if $g\in H$![]() , then $\mathrm {cl}_{\mathsf {S}_H}(g)=\{g,\,g^{m},\,g^{m^{2}},\,\dotsc \}$
, then $\mathrm {cl}_{\mathsf {S}_H}(g)=\{g,\,g^{m},\,g^{m^{2}},\,\dotsc \}$![]() . We denote this supercharacter theory by $[H]_m$
. We denote this supercharacter theory by $[H]_m$![]() . Given an integer $m$
. Given an integer $m$![]() and $g\in G$
and $g\in G$![]() , we let $[g]_m$
, we let $[g]_m$![]() denote the set $\{g,\,g^{m},\,g^{m^{2}},\,\dotsc \}$
denote the set $\{g,\,g^{m},\,g^{m^{2}},\,\dotsc \}$![]() . We let $\lvert {m}\rvert_p$
. We let $\lvert {m}\rvert_p$![]() denote the order of $m$
denote the order of $m$![]() modulo $p$
modulo $p$![]() , which is also the size of $[g]_m$
, which is also the size of $[g]_m$![]() for $1\ne g\in G$
for $1\ne g\in G$![]() .
.
Lemma 6.3 Let $\mathsf {S}$![]() have exactly two $\mathsf {S}$
have exactly two $\mathsf {S}$![]() -normal subgroups $H$
-normal subgroups $H$![]() and $N$
and $N$![]() . Write $\mathsf {S}_H=[H]_{m_1}$
. Write $\mathsf {S}_H=[H]_{m_1}$![]() and $\mathsf {S}_N=[N]_{m_2}$
and $\mathsf {S}_N=[N]_{m_2}$![]() . Let $d_i=\lvert{m_i}\rvert_p$
. Let $d_i=\lvert{m_i}\rvert_p$![]() , $i=1,\,2$
, $i=1,\,2$![]() , and assume that $(d_1,\,d_2)=1$
, and assume that $(d_1,\,d_2)=1$![]() . Then $\mathsf {S}=\mathsf {S}_H\times \mathsf {S}_N$
. Then $\mathsf {S}=\mathsf {S}_H\times \mathsf {S}_N$![]() . In particular, $\mathsf {S}$
. In particular, $\mathsf {S}$![]() comes from automorphisms.
comes from automorphisms.
Proof. Let $g\in G\setminus (H\cup N)$![]() . Then $d_2=\lvert {\mathrm {cl}_{\mathsf {S}_{G/H}}(g)}\rvert$
. Then $d_2=\lvert {\mathrm {cl}_{\mathsf {S}_{G/H}}(g)}\rvert$![]() and $d_1=\lvert {\mathrm {cl}_{\mathsf {S}_{G/N}}(g)}\rvert$
and $d_1=\lvert {\mathrm {cl}_{\mathsf {S}_{G/N}}(g)}\rvert$![]() . So $d_1d_2=\mathrm {lcm}(d_1,\,d_1)$
. So $d_1d_2=\mathrm {lcm}(d_1,\,d_1)$![]() divides $\lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert$
divides $\lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert$![]() . Since $\mathsf {S}\preccurlyeq \mathsf {S}_H\times \mathsf {S}_N$
. Since $\mathsf {S}\preccurlyeq \mathsf {S}_H\times \mathsf {S}_N$![]() , we know $\mathrm {cl}_{\mathsf {S}}(g)\subseteq \mathrm {cl}_{\mathsf {S}_H\times \mathsf {S}_N}(g)$
, we know $\mathrm {cl}_{\mathsf {S}}(g)\subseteq \mathrm {cl}_{\mathsf {S}_H\times \mathsf {S}_N}(g)$![]() . Since $d_1d_2\le \lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert \le \lvert {\mathrm {cl}_{\mathsf {S}_H\times \mathsf {S}_N}(g)}\rvert =d_1d_2$
. Since $d_1d_2\le \lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert \le \lvert {\mathrm {cl}_{\mathsf {S}_H\times \mathsf {S}_N}(g)}\rvert =d_1d_2$![]() , we conclude that $\mathrm {cl}_{\mathsf {S}}(g)=\mathrm {cl}_{\mathsf {S}_H\times \mathsf {S}_N}(g)$
, we conclude that $\mathrm {cl}_{\mathsf {S}}(g)=\mathrm {cl}_{\mathsf {S}_H\times \mathsf {S}_N}(g)$![]() . Hence $\mathsf {S}=\mathsf {S}_H\times \mathsf {S}_N$
. Hence $\mathsf {S}=\mathsf {S}_H\times \mathsf {S}_N$![]() , and the result follows from Lemma 4.1.
, and the result follows from Lemma 4.1.
We suspect that the condition $(d_1,\,d_2)=1$![]() in Lemma 6.3 can be strengthened to $(d_1,\,d_2)< p-1$
in Lemma 6.3 can be strengthened to $(d_1,\,d_2)< p-1$![]() . This has only been totally verified for the primes $p=2,\,3$
. This has only been totally verified for the primes $p=2,\,3$![]() and $5$
and $5$![]() .
.
Now suppose that there are at least three $\mathsf {S}$![]() -normal subgroups. We conjecture that $\mathsf {S}$
-normal subgroups. We conjecture that $\mathsf {S}$![]() comes from automorphisms whenever the restriction to a $\mathsf {S}$
comes from automorphisms whenever the restriction to a $\mathsf {S}$![]() -normal subgroup is not the coarsest theory.
-normal subgroup is not the coarsest theory.
Conjecture 6.4 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() . Suppose that $G$
. Suppose that $G$![]() has at least three non-trivial, proper $\mathsf {S}$
has at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups, and let $H$
-normal subgroups, and let $H$![]() be one of them. If $\mathsf {S}_H\neq \mathsf {M}(H)$
be one of them. If $\mathsf {S}_H\neq \mathsf {M}(H)$![]() , then every subgroup of $G$
, then every subgroup of $G$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal. In particular, $\mathsf {S}$
-normal. In particular, $\mathsf {S}$![]() comes from automorphisms.
comes from automorphisms.
Although a general proof appears to be difficult, this can be proved rather easily in a couple of specific cases.
Lemma 6.5 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() . Suppose that $G$
. Suppose that $G$![]() has at least three non-trivial, proper $\mathsf {S}$
has at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups. Let $H$
-normal subgroups. Let $H$![]() be $\mathsf {S}$
be $\mathsf {S}$![]() -normal and write $\mathsf {S}_H=[H]_m$
-normal and write $\mathsf {S}_H=[H]_m$![]() . If $\lvert {m}\rvert _p=1$
. If $\lvert {m}\rvert _p=1$![]() or $2,$
or $2,$![]() then Conjecture 6.4 holds.
then Conjecture 6.4 holds.
Proof. First assume that $\lvert {m}\rvert _p=1$![]() , and let $K$
, and let $K$![]() be another $\mathsf {S}$
be another $\mathsf {S}$![]() -normal subgroup. Then $\mathsf {S}_K=\mathsf {m}(K)$
-normal subgroup. Then $\mathsf {S}_K=\mathsf {m}(K)$![]() , so $G=\langle{H,\,K}\rangle\le Z(\mathsf {S})$
, so $G=\langle{H,\,K}\rangle\le Z(\mathsf {S})$![]() .
.
Now assume that $\lvert {m} \rvert_p=2$![]() . We may find distinct non-identity elements $x,\,y\in G$
. We may find distinct non-identity elements $x,\,y\in G$![]() such that $\langle{x}\rangle$
such that $\langle{x}\rangle$![]() , $\langle{y}\rangle$
, $\langle{y}\rangle$![]() and $\langle{xy}\rangle$
and $\langle{xy}\rangle$![]() are all $\mathsf {S}$
are all $\mathsf {S}$![]() -normal. We show by induction on $n$
-normal. We show by induction on $n$![]() that $\langle {xy^{n}}\rangle$
that $\langle {xy^{n}}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal for every $n\ge 1$
-normal for every $n\ge 1$![]() . Let $[g]$
. Let $[g]$![]() denote the set $\{g,\,g^{-1}\}$
denote the set $\{g,\,g^{-1}\}$![]() for $g\in G$
for $g\in G$![]() . Let $n\ge 2$
. Let $n\ge 2$![]() be the smallest integer for which $\langle {xy^{n}}\rangle$
be the smallest integer for which $\langle {xy^{n}}\rangle$![]() is not $\mathsf {S}$
is not $\mathsf {S}$![]() -normal. Then $\langle {xy^{n-1}}\rangle$
-normal. Then $\langle {xy^{n-1}}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, which means that $\widehat {[xy^{n-1}]}\widehat {[y]}$
-normal, which means that $\widehat {[xy^{n-1}]}\widehat {[y]}$![]() can be expressed as a non-negative integer linear combination of $\mathsf {S}$
can be expressed as a non-negative integer linear combination of $\mathsf {S}$![]() -class sums. Since $\widehat {[xy^{n-1}]}\widehat {[y]}=\widehat {[xy^{n}]}+\widehat {[xy^{n-2}]}$
-class sums. Since $\widehat {[xy^{n-1}]}\widehat {[y]}=\widehat {[xy^{n}]}+\widehat {[xy^{n-2}]}$![]() and $\langle {xy^{n-2}}\rangle$
and $\langle {xy^{n-2}}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, $[xy^{n}]$
-normal, $[xy^{n}]$![]() must be a union of $\mathsf {S}$
must be a union of $\mathsf {S}$![]() -classes. So $\langle {[xy^{n}]}\rangle=\langle {xy^{n}}\rangle$
-classes. So $\langle {[xy^{n}]}\rangle=\langle {xy^{n}}\rangle$![]() is also $\mathsf {S}$
is also $\mathsf {S}$![]() -normal, which contradicts the choice of $n$
-normal, which contradicts the choice of $n$![]() . Thus, $\langle {xy^{n}}\rangle$
. Thus, $\langle {xy^{n}}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal for every integer $n$
-normal for every integer $n$![]() , as claimed.
, as claimed.
Conjecture 6.4 also holds in the case that $\mathsf {S}$![]() comes from automorphisms.
comes from automorphisms.
Lemma 6.6 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() coming from automorphisms. If $G$
coming from automorphisms. If $G$![]() has at least three non-trivial, proper $\mathsf {S}$
has at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups, then every subgroup of $G$
-normal subgroups, then every subgroup of $G$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal.
-normal.
Proof. Suppose that $\mathsf {S}$![]() comes from $A\le \mathrm {Aut}(G)$
comes from $A\le \mathrm {Aut}(G)$![]() . Let $H_i$
. Let $H_i$![]() , $i=1,\,2,\,3$
, $i=1,\,2,\,3$![]() , be $\mathsf {S}$
, be $\mathsf {S}$![]() -normal of order $p$
-normal of order $p$![]() . We may assume that $H_1$
. We may assume that $H_1$![]() is generated by $x$
is generated by $x$![]() , $H_2$
, $H_2$![]() is generated by $y$
is generated by $y$![]() and $H_3$
and $H_3$![]() is generated by $xy$
is generated by $xy$![]() . Let $a\in A$
. Let $a\in A$![]() . Since $H_1$
. Since $H_1$![]() and $H_2$
and $H_2$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -normal, there exist integers $i$
-normal, there exist integers $i$![]() and $j$
and $j$![]() so that $x^{a}=x^{i}$
so that $x^{a}=x^{i}$![]() and $y^{a}=y^{j}$
and $y^{a}=y^{j}$![]() . Then $(xy)^{a}=x^{i}y^{j}$
. Then $(xy)^{a}=x^{i}y^{j}$![]() . Since $H_3$
. Since $H_3$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, $(xy)^{a}\in \langle {xy}\rangle$
-normal, $(xy)^{a}\in \langle {xy}\rangle$![]() , which forces $i=j$
, which forces $i=j$![]() . We conclude that $a\in Z(\mathrm {Aut}(G))$
. We conclude that $a\in Z(\mathrm {Aut}(G))$![]() and hence fixes every subgroup of $G$
and hence fixes every subgroup of $G$![]() .
.
We remark that Lemma 6.6 also follows from [Reference Wielandt23, Lemma 26.3], a result about Schur rings.
We now outline a strategy we believe will work to prove Conjecture 6.4, although the actual proof has evaded us. This strategy involves an algorithm of the first author appearing in [Reference Burkett4], which we now describe. We begin by defining an equivalence relation on $G$![]() coming from a partial partition of $G$
coming from a partial partition of $G$![]() . Let $\mathcal {C}$
. Let $\mathcal {C}$![]() be a $G$
be a $G$![]() -invariant partial partition of $G$
-invariant partial partition of $G$![]() . For $K,\,L\in \mathcal {C}$
. For $K,\,L\in \mathcal {C}$![]() and $g\in G$
and $g\in G$![]() , define
, define
Also, recall that for $K\subseteq G$![]() , $\hat {K}$
, $\hat {K}$![]() denotes the element $\sum \nolimits _{g\in K}g$
denotes the element $\sum \nolimits _{g\in K}g$![]() of the group algebra $\mathbb {Z}(G)$
of the group algebra $\mathbb {Z}(G)$![]() .
.
Define an equivalence relation $\sim$![]() on $G$
on $G$![]() by defining $g\sim h$
by defining $g\sim h$![]() if and only if
if and only if
for all $K,\,L\in \mathcal {C}$![]() . Let $\mathscr {K}(\mathcal {C})$
. Let $\mathscr {K}(\mathcal {C})$![]() denote the set of equivalence classes of $\mathrm {Irr}(G)$
denote the set of equivalence classes of $\mathrm {Irr}(G)$![]() under $\sim$
under $\sim$![]() . It is shown in [Reference Burkett4] that $\mathscr {K}(\mathcal {C})$
. It is shown in [Reference Burkett4] that $\mathscr {K}(\mathcal {C})$![]() is a refinement of $\mathcal {C}$
is a refinement of $\mathcal {C}$![]() and that $\mathscr {K}(\mathcal {C})=\mathcal {C}$
and that $\mathscr {K}(\mathcal {C})=\mathcal {C}$![]() if and only if $\mathcal {C}$
if and only if $\mathcal {C}$![]() is the set of superclasses for a supercharacter theory $\mathsf {S}$
is the set of superclasses for a supercharacter theory $\mathsf {S}$![]() of $G$
of $G$![]() . If the partition $\mathrm {Cl}(\mathsf {S})$
. If the partition $\mathrm {Cl}(\mathsf {S})$![]() of $G$
of $G$![]() corresponding to the supercharacter theory $\mathsf {S}$
corresponding to the supercharacter theory $\mathsf {S}$![]() of $G$
of $G$![]() is a refinement of $\mathcal {C}$
is a refinement of $\mathcal {C}$![]() , then $\mathrm {Cl}(\mathsf {S})$
, then $\mathrm {Cl}(\mathsf {S})$![]() is a refinement of $\mathscr {K}(\mathcal {C})$
is a refinement of $\mathscr {K}(\mathcal {C})$![]() . Iterating on this process, the sequence $\mathcal {C},\, \mathscr {K}(\mathcal {C}),\, \mathscr {K}^{2}(\mathcal {C}),\,\dotsc$
. Iterating on this process, the sequence $\mathcal {C},\, \mathscr {K}(\mathcal {C}),\, \mathscr {K}^{2}(\mathcal {C}),\,\dotsc$![]() eventually terminates; call its terminal member $\mathscr {K}^{\infty }(\mathcal {C})$
eventually terminates; call its terminal member $\mathscr {K}^{\infty }(\mathcal {C})$![]() . Then $\mathscr {K}^{\infty }(\mathcal {C})$
. Then $\mathscr {K}^{\infty }(\mathcal {C})$![]() is the set of superclasses for a supercharacter theory $\mathsf {T}$
is the set of superclasses for a supercharacter theory $\mathsf {T}$![]() of $G$
of $G$![]() , and $\mathsf {S}\preccurlyeq \mathsf {T}$
, and $\mathsf {S}\preccurlyeq \mathsf {T}$![]() .
.
Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() , and assume that $H_1,\,H_2,\,H_3$
, and assume that $H_1,\,H_2,\,H_3$![]() are distinct non-trivial, proper $\mathsf {S}$
are distinct non-trivial, proper $\mathsf {S}$![]() -normal subgroups. Assume further that $\mathsf {S}_{H_1}\ne \mathsf {M}(H_1)$
-normal subgroups. Assume further that $\mathsf {S}_{H_1}\ne \mathsf {M}(H_1)$![]() . Let $r$
. Let $r$![]() be a primitive root modulo $p$
be a primitive root modulo $p$![]() . If $\mathsf {S}_{H_1}=[H_1]_m$
. If $\mathsf {S}_{H_1}=[H_1]_m$![]() , then $[H_1]_m\preccurlyeq [H_1]_{r^{2}}$
, then $[H_1]_m\preccurlyeq [H_1]_{r^{2}}$![]() , since $\mathsf {S}_{H_1}\ne \mathsf {M}(H_1)$
, since $\mathsf {S}_{H_1}\ne \mathsf {M}(H_1)$![]() . In particular, $\mathrm {Cl}(\mathsf {S})$
. In particular, $\mathrm {Cl}(\mathsf {S})$![]() is a refinement of the partition $\bigcup _{i=1}^{3}[H_i]_m\cup \{G\setminus \bigcup _{i=1}^{3}H_i\}$
is a refinement of the partition $\bigcup _{i=1}^{3}[H_i]_m\cup \{G\setminus \bigcup _{i=1}^{3}H_i\}$![]() , which is a refinement of the partition $\mathcal {C}=\bigcup _{i=1}^{3}[H_i]_{r^{2}}\cup \{G\setminus \bigcup _{i=1}^{3}H_i\}$
, which is a refinement of the partition $\mathcal {C}=\bigcup _{i=1}^{3}[H_i]_{r^{2}}\cup \{G\setminus \bigcup _{i=1}^{3}H_i\}$![]() . If $g\in G\setminus \bigcup _{i=1}^{n}H_i$
. If $g\in G\setminus \bigcup _{i=1}^{n}H_i$![]() such that $[g]_{r^{2}}\in \mathscr {K}^{\infty }(\mathcal {C})$
such that $[g]_{r^{2}}\in \mathscr {K}^{\infty }(\mathcal {C})$![]() , then $[g]_{r^{2}}$
, then $[g]_{r^{2}}$![]() must be a union of $\mathsf {S}$
must be a union of $\mathsf {S}$![]() -classes. Thus, $\langle {[g]_{r^{2}}}\rangle =\langle {g}\rangle$
-classes. Thus, $\langle {[g]_{r^{2}}}\rangle =\langle {g}\rangle$![]() is another $\mathsf {S}$
is another $\mathsf {S}$![]() -normal subgroup.
-normal subgroup.
Conjecture 6.7 Let $H_1,\,H_2$![]() and $H_3$
and $H_3$![]() be distinct subgroups of $G$
be distinct subgroups of $G$![]() of order $p$
of order $p$![]() . Let $r$
. Let $r$![]() be a primitive root modulo $p$
be a primitive root modulo $p$![]() . Define $\mathcal {C}=\bigcup _{i=1}^{3}[H_i]_{r^{2}}\cup \{G\setminus \bigcup _{i=1}^{3}H_i\}$
. Define $\mathcal {C}=\bigcup _{i=1}^{3}[H_i]_{r^{2}}\cup \{G\setminus \bigcup _{i=1}^{3}H_i\}$![]() . For every $g\in G\setminus \bigcup _iH_i$
. For every $g\in G\setminus \bigcup _iH_i$![]() , the set $[g]_{r^{2}}$
, the set $[g]_{r^{2}}$![]() lies in $\mathscr {K}^{\infty }(\mathcal {C})$
lies in $\mathscr {K}^{\infty }(\mathcal {C})$![]() .
.
We now illustrate a few small examples illustrating the statement of Conjecture 6.7.
Example 6.8 Let $G=\langle {x,\,y}\rangle$![]() be the group $C_5\times C_5$
be the group $C_5\times C_5$![]() . Suppose that $\mathsf {S}$
. Suppose that $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() with at least three supernormal subgroups $H_1$
with at least three supernormal subgroups $H_1$![]() , $H_2$
, $H_2$![]() and $H_3$
and $H_3$![]() . Relabeling if necessary, we may write $H_1=\langle {x}\rangle$
. Relabeling if necessary, we may write $H_1=\langle {x}\rangle$![]() , $H_2=\langle {y}\rangle$
, $H_2=\langle {y}\rangle$![]() and $H_3=\langle {xy}\rangle$
and $H_3=\langle {xy}\rangle$![]() . If $\mathsf {S}_{H_1}\ne \mathsf {M}(H_1)$
. If $\mathsf {S}_{H_1}\ne \mathsf {M}(H_1)$![]() , then $\mathsf {S}_{H_1}$
, then $\mathsf {S}_{H_1}$![]() comes from the inversion automorphism. So $[x]_4$
comes from the inversion automorphism. So $[x]_4$![]() and $[y]_4$
and $[y]_4$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -classes. So
-classes. So
is a sum of $\mathsf {S}$![]() -class sums. Since $\langle {xy}\rangle$
-class sums. Since $\langle {xy}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, it follows that $L_1=[xy^{-1}]_4$
-normal, it follows that $L_1=[xy^{-1}]_4$![]() is a union of $\mathsf {S}$
is a union of $\mathsf {S}$![]() -classes. Thus, so is $L_1^{i}=[x^{i}y^{-i}]_4$
-classes. Thus, so is $L_1^{i}=[x^{i}y^{-i}]_4$![]() for each $2\le i\le p-1$
for each $2\le i\le p-1$![]() . Since $\langle {xy^{-1}}\rangle = \bigcup _iL_1^{i}$
. Since $\langle {xy^{-1}}\rangle = \bigcup _iL_1^{i}$![]() , we deduce that $\langle {xy^{-1}}\rangle$
, we deduce that $\langle {xy^{-1}}\rangle$![]() is also $\mathsf {S}$
is also $\mathsf {S}$![]() -normal.
-normal.
Similarly, $[y]_4$![]() and $[xy]_4$
and $[xy]_4$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -classes. Thus,
-classes. Thus,
is a union of $\mathsf {S}$![]() -classes. Since $\langle {x}\rangle$
-classes. Since $\langle {x}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, $[xy^{2}]_4^{i}=\{x^{i}y^{2i},\,x^{-i}y^{-2i}\}$
-normal, $[xy^{2}]_4^{i}=\{x^{i}y^{2i},\,x^{-i}y^{-2i}\}$![]() is a union of $\mathsf {S}$
is a union of $\mathsf {S}$![]() -classes for each $2\le i\le p-1$
-classes for each $2\le i\le p-1$![]() . From this, we conclude that $\langle {xy^{2}}\rangle$
. From this, we conclude that $\langle {xy^{2}}\rangle$![]() is also $\mathsf {S}$
is also $\mathsf {S}$![]() -normal.
-normal.
Using a similar technique with the classes $[y^{2}]_4$![]() and $[xy]_4$
and $[xy]_4$![]() , we can also show that $\langle {xy^{3}}\rangle$
, we can also show that $\langle {xy^{3}}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal.
-normal.
Example 6.9 Let $G=\langle {x,\,y}\rangle$![]() be the group $C_7\times C_7$
be the group $C_7\times C_7$![]() . Suppose that $\mathsf {S}$
. Suppose that $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() with at least three supernormal subgroups. As with the previous example, we may assume $H_1=\langle {x}\rangle$
with at least three supernormal subgroups. As with the previous example, we may assume $H_1=\langle {x}\rangle$![]() , $H_2=\langle{y}\rangle$
, $H_2=\langle{y}\rangle$![]() and $H_3=\langle {xy}\rangle$
and $H_3=\langle {xy}\rangle$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -normal. Suppose that $\mathsf {S}_{H_1}$
-normal. Suppose that $\mathsf {S}_{H_1}$![]() comes from the squaring automorphism. Then $[x]_2=\{x,\,x^{2},\,x^{4}\}$
comes from the squaring automorphism. Then $[x]_2=\{x,\,x^{2},\,x^{4}\}$![]() and $[y]_2=\{y,\,y^{2},\,y^{4}\}$
and $[y]_2=\{y,\,y^{2},\,y^{4}\}$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -classes. So
-classes. So
is a sum of $\mathsf {S}$![]() -classes. Since $\langle {xy}\rangle$
-classes. Since $\langle {xy}\rangle$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, $L_1=[xy^{2}]_2\cup [xy^{4}]_2$
-normal, $L_1=[xy^{2}]_2\cup [xy^{4}]_2$![]() is a union of $\mathsf {S}$
is a union of $\mathsf {S}$![]() -classes. Similarly, using the $\mathsf {S}$
-classes. Similarly, using the $\mathsf {S}$![]() -classes of $y^{-1}$
-classes of $y^{-1}$![]() and $xy$
and $xy$![]() , we see that $L_2=[xy^{4}]_2\cup [xy^{-1}]_2$
, we see that $L_2=[xy^{4}]_2\cup [xy^{-1}]_2$![]() is a union of $\mathsf {S}$
is a union of $\mathsf {S}$![]() -classes. So $L=L_1\cap L_2=[xy^{4}]_2$
-classes. So $L=L_1\cap L_2=[xy^{4}]_2$![]() is a union of $\mathsf {S}$
is a union of $\mathsf {S}$![]() -classes. Thus, we may conclude that $\langle {xy^{4}}\rangle,\, \langle {xy^{2}}\rangle$
-classes. Thus, we may conclude that $\langle {xy^{4}}\rangle,\, \langle {xy^{2}}\rangle$![]() and $\langle {xy^{-1}}\rangle$
and $\langle {xy^{-1}}\rangle$![]() are also $\mathsf {S}$
are also $\mathsf {S}$![]() -normal.
-normal.
One may easily verify that a similar process shows that every subgroup of $G$![]() must be $\mathsf {S}$
must be $\mathsf {S}$![]() -normal.
-normal.
Example 6.10 Let $G=\langle {x,\,y}\rangle$![]() be the group $C_{11}\times C_{11}$
be the group $C_{11}\times C_{11}$![]() . Suppose that $\mathsf {S}$
. Suppose that $\mathsf {S}$![]() is a supercharacter theory of $G$
is a supercharacter theory of $G$![]() with at least three supernormal subgroups $H_1,\,H_2$
with at least three supernormal subgroups $H_1,\,H_2$![]() and $H_3$
and $H_3$![]() , and suppose that $\mathsf {S}_{H_1}=[H_1]_3$
, and suppose that $\mathsf {S}_{H_1}=[H_1]_3$![]() . As with the previous example, we may assume $H_1=\langle {x}\rangle$
. As with the previous example, we may assume $H_1=\langle {x}\rangle$![]() , $H_2=\langle {y}\rangle$
, $H_2=\langle {y}\rangle$![]() and $H_3=\langle {xy}\rangle$
and $H_3=\langle {xy}\rangle$![]() . Let $\mathcal {C}$
. Let $\mathcal {C}$![]() be the partition
be the partition
of $G$![]() . Note that $\mathsf {S}$
. Note that $\mathsf {S}$![]() is a refinement of $\mathcal {C}$
is a refinement of $\mathcal {C}$![]() . It is routine to show that
. It is routine to show that

and that

Since $\widehat {[xy^{4}]_3}$![]() does not appear in the above decomposition and $\mathsf {S}$
does not appear in the above decomposition and $\mathsf {S}$![]() is a refinement of $\mathscr {K}^{2}(\mathcal {C})$
is a refinement of $\mathscr {K}^{2}(\mathcal {C})$![]() , we conclude that $\langle {xy^{4}}\rangle$
, we conclude that $\langle {xy^{4}}\rangle$![]() and $\langle {xy^{5}}\rangle$
and $\langle {xy^{5}}\rangle$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -normal. Similarly, $\langle {xy^{7}}\rangle$
-normal. Similarly, $\langle {xy^{7}}\rangle$![]() and $\langle {xy^{8}}\rangle$
and $\langle {xy^{8}}\rangle$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -normal. The same reasoning also shows that $\langle {xy^{3}}\rangle$
-normal. The same reasoning also shows that $\langle {xy^{3}}\rangle$![]() and $\langle {xy^{9}}\rangle$
and $\langle {xy^{9}}\rangle$![]() are $\mathsf {S}$
are $\mathsf {S}$![]() -normal.
-normal.
Since $\widehat {[xy^{2}]_3}$![]() does not appear in the above decomposition, and since $\widehat {[xy^{6}]_3}$
does not appear in the above decomposition, and since $\widehat {[xy^{6}]_3}$![]() and $\widehat {[xy^{10}]_3}$
and $\widehat {[xy^{10}]_3}$![]() appear with different coefficients, we see that $\langle {xy^{2}}\rangle$
appear with different coefficients, we see that $\langle {xy^{2}}\rangle$![]() , $\langle {xy^{6}}\rangle$
, $\langle {xy^{6}}\rangle$![]() and $\langle {xy^{10}}\rangle$
and $\langle {xy^{10}}\rangle$![]() are also $\mathsf {S}$
are also $\mathsf {S}$![]() -normal. Thus, every subgroup of $G$
-normal. Thus, every subgroup of $G$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal.
-normal.
We have verified Conjecture 6.7 for every prime $p\le 47$![]() using the method outlined above, thereby also verifying Conjecture 6.4 in the process. In the event that Conjecture 6.4 holds, we can conclude that a large collection of supercharacter theories of $G$
using the method outlined above, thereby also verifying Conjecture 6.4 in the process. In the event that Conjecture 6.4 holds, we can conclude that a large collection of supercharacter theories of $G$![]() must come from automorphisms.
must come from automorphisms.
Lemma 6.11 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() . If every subgroup of $G$
. If every subgroup of $G$![]() is $\mathsf {S}$
is $\mathsf {S}$![]() -normal, then $\mathsf {S}$
-normal, then $\mathsf {S}$![]() comes from automorphisms.
comes from automorphisms.
Proof. Let $H_1$![]() , $H_2$
, $H_2$![]() and $H_3$
and $H_3$![]() be distinct subgroups of $G$
be distinct subgroups of $G$![]() . Suppose that $\mathsf {S}_{H_1}$
. Suppose that $\mathsf {S}_{H_1}$![]() comes from the automorphism that sends an element to its $m^{\rm th}$
comes from the automorphism that sends an element to its $m^{\rm th}$![]() power. Let $\phi _{12}:H_1\to G/H_2$
power. Let $\phi _{12}:H_1\to G/H_2$![]() , $\phi _{13}:H_1\to G/H_3$
, $\phi _{13}:H_1\to G/H_3$![]() and $\phi _{23}:H_2\to G/H_3$
and $\phi _{23}:H_2\to G/H_3$![]() be the canonical isomorphisms. The $\mathsf {S}_{G/H_2}$
be the canonical isomorphisms. The $\mathsf {S}_{G/H_2}$![]() -classes are the images of the $\mathsf {S}_{H_1}$
-classes are the images of the $\mathsf {S}_{H_1}$![]() -classes under $\phi _{12}$
-classes under $\phi _{12}$![]() and the $\mathsf {S}_{G/H_3}$
and the $\mathsf {S}_{G/H_3}$![]() -classes are the images of the $\mathsf {S}_{H_2}$
-classes are the images of the $\mathsf {S}_{H_2}$![]() -classes under $\phi _{23}$
-classes under $\phi _{23}$![]() . So the $\mathsf {S}_{H_2}$
. So the $\mathsf {S}_{H_2}$![]() -classes are the images of the $\mathsf {S}_{H_1}$
-classes are the images of the $\mathsf {S}_{H_1}$![]() -classes under $\phi _{23}^{-1}\phi _{12}$
-classes under $\phi _{23}^{-1}\phi _{12}$![]() . Thus, $\mathsf {S}_{H_2}$
. Thus, $\mathsf {S}_{H_2}$![]() also comes from the automorphism that sends an element to its $m^{\rm th}$
also comes from the automorphism that sends an element to its $m^{\rm th}$![]() power. Since $H_2$
power. Since $H_2$![]() was chosen randomly, it follows that the $\mathsf {S}$
was chosen randomly, it follows that the $\mathsf {S}$![]() -class of an element $g\in G$
-class of an element $g\in G$![]() is just $\{g,\,g^{m},\,g^{m^{2}},\,\dotsc \}$
is just $\{g,\,g^{m},\,g^{m^{2}},\,\dotsc \}$![]() . So $\mathsf {S}$
. So $\mathsf {S}$![]() comes from automorphisms, as claimed.
comes from automorphisms, as claimed.
We have observed in small cases ($p=2,\,3,\,5$![]() ) that every supercharacter theory either comes from automorphisms or is a partition supercharacter theory. Due the large number of conjugacy classes in $C_7\times C_7$
) that every supercharacter theory either comes from automorphisms or is a partition supercharacter theory. Due the large number of conjugacy classes in $C_7\times C_7$![]() , it is unfortunately rather difficult computationally to verify the observation in this case. It is known (e.g., by [Reference Diaconis and Isaacs7, Theorem 2.2 (f)]) that if $e$
, it is unfortunately rather difficult computationally to verify the observation in this case. It is known (e.g., by [Reference Diaconis and Isaacs7, Theorem 2.2 (f)]) that if $e$![]() is an integer coprime to $p$
is an integer coprime to $p$![]() , then $K^{e}=\{g^{e}:g\in G\}$
, then $K^{e}=\{g^{e}:g\in G\}$![]() is an $\mathsf {S}$
is an $\mathsf {S}$![]() -class for every $\mathsf {S}$
-class for every $\mathsf {S}$![]() -class $K$
-class $K$![]() . In every example we have computed, a very special choice of $e$
. In every example we have computed, a very special choice of $e$![]() actually fixes every $\mathsf {S}$
actually fixes every $\mathsf {S}$![]() -class as long as $G$
-class as long as $G$![]() has at least three non-trivial, proper $\mathsf {S}$
has at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups. Thus, the following conjecture seems reasonable, and would allow us to greatly reduce the possible structure of supercharacter theories of $G$
-normal subgroups. Thus, the following conjecture seems reasonable, and would allow us to greatly reduce the possible structure of supercharacter theories of $G$![]() .
.
Conjecture 6.12 Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() with at least three non-trivial, proper $\mathsf {S}$
with at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups. Let $H$
-normal subgroups. Let $H$![]() be a non-trivial $\mathsf {S}$
be a non-trivial $\mathsf {S}$![]() -normal subgroup and write $\mathsf {S}_H=[H]_m$
-normal subgroup and write $\mathsf {S}_H=[H]_m$![]() . Let $\mathsf {T}$
. Let $\mathsf {T}$![]() be the supercharacter theory of $G$
be the supercharacter theory of $G$![]() coming from the automorphism sending an element to its $m^{\rm th}$
coming from the automorphism sending an element to its $m^{\rm th}$![]() power. Then $\mathsf {T}\preccurlyeq \mathsf {S}$
power. Then $\mathsf {T}\preccurlyeq \mathsf {S}$![]() .
.
Proposition 6.13 Assume Conjecture 6.12 holds. Let $\mathsf {S}$![]() be a supercharacter theory of $G$
be a supercharacter theory of $G$![]() with at least three non-trivial, proper $\mathsf {S}$
with at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups. Suppose that $\mathsf {S}_H=\mathsf {M}(H)$
-normal subgroups. Suppose that $\mathsf {S}_H=\mathsf {M}(H)$![]() for every $\mathsf {S}$
for every $\mathsf {S}$![]() -normal subgroup $H$
-normal subgroup $H$![]() of $G$
of $G$![]() . Then $\mathsf {S}$
. Then $\mathsf {S}$![]() is a partition supercharacter theory.
is a partition supercharacter theory.
Proof. Let $H_1,\,H_2,\,\dotsc,\, H_n$![]() be the $\mathsf {S}$
be the $\mathsf {S}$![]() -normal subgroups of $G$
-normal subgroups of $G$![]() of order $p$
of order $p$![]() . Let $g\in G\setminus \bigcup _iH_i$
. Let $g\in G\setminus \bigcup _iH_i$![]() . Let $r$
. Let $r$![]() be a primitive root modulo $p$
be a primitive root modulo $p$![]() and note that $\mathsf {S}_{H_i}$
and note that $\mathsf {S}_{H_i}$![]() comes from the automorphism sending an element to its $r^{\rm th}$
comes from the automorphism sending an element to its $r^{\rm th}$![]() power for each $1\le i\le n$
power for each $1\le i\le n$![]() . By hypothesis, Conjecture 6.12 holds, so $\mathsf {T}\preccurlyeq \mathsf {S}$
. By hypothesis, Conjecture 6.12 holds, so $\mathsf {T}\preccurlyeq \mathsf {S}$![]() where $\mathsf {T}$
where $\mathsf {T}$![]() is the supercharacter theory of $G$
is the supercharacter theory of $G$![]() coming from the automorphism sending an element to its $r^{\rm th}$
coming from the automorphism sending an element to its $r^{\rm th}$![]() power. Observe that $\mathsf {T}$
power. Observe that $\mathsf {T}$![]() is the partition supercharacter theory $\mathsf {S}_{\mathcal {P}}$
is the partition supercharacter theory $\mathsf {S}_{\mathcal {P}}$![]() corresponding to the partition $\mathcal {P}$
corresponding to the partition $\mathcal {P}$![]() consisting of all singletons. The result now follows from Lemma 5.2.
consisting of all singletons. The result now follows from Lemma 5.2.
7. Computations for small primes
In this section, we consider the cases $p=2,\,3,\,5,\,7$![]() and $11$
and $11$![]() in some depth. For $p=2,\,3$
in some depth. For $p=2,\,3$![]() and $5$
and $5$![]() , we can fully classify the supercharacter theories of $C_p\times C_p$
, we can fully classify the supercharacter theories of $C_p\times C_p$![]() . We are able to fully classify the supercharacter theories of $C_7\times C_7$
. We are able to fully classify the supercharacter theories of $C_7\times C_7$![]() that have at least three non-trivial, proper supernormal subgroups. This allows us to verify Conjecture 6.12 for the case $p=7$
that have at least three non-trivial, proper supernormal subgroups. This allows us to verify Conjecture 6.12 for the case $p=7$![]() .
.
As mentioned earlier, we have verified Conjecture 6.4 for all primes $p\le 47$![]() . So we can classify the supercharacter theories of $C_{11}\times C_{11}$
. So we can classify the supercharacter theories of $C_{11}\times C_{11}$![]() that have at least three non-trivial, proper supernormal subgroups and for which the restriction to one of them is not the coarsest theory. We do a little more for $p=11$
that have at least three non-trivial, proper supernormal subgroups and for which the restriction to one of them is not the coarsest theory. We do a little more for $p=11$![]() . We classify all supercharacter theories of $C_{11}\times C_{11}$
. We classify all supercharacter theories of $C_{11}\times C_{11}$![]() that have at least nine non-trivial, proper supernormal subgroups.
that have at least nine non-trivial, proper supernormal subgroups.
We will say that a supercharacter theory $\mathsf {S}$![]() has type $T_n$
has type $T_n$![]() if $G$
if $G$![]() has exactly $n$
has exactly $n$![]() non-trivial, proper $\mathsf {S}$
non-trivial, proper $\mathsf {S}$![]() -normal subgroups. In each of the cases just mentioned, we list the total number of supercharacter theories of type $T_n$
-normal subgroups. In each of the cases just mentioned, we list the total number of supercharacter theories of type $T_n$![]() . For each $n$
. For each $n$![]() , we divide the supercharacter theories of type $T_n$
, we divide the supercharacter theories of type $T_n$![]() into three major types: (1) Those that can be realized as a non-trivial $\ast$
into three major types: (1) Those that can be realized as a non-trivial $\ast$![]() or direct product; (2) Those coming from automorphisms (automorphic supercharacter theories); (3) Those coming from partitions. We give exact counts for each type as well.
or direct product; (2) Those coming from automorphisms (automorphic supercharacter theories); (3) Those coming from partitions. We give exact counts for each type as well.
Before discussing the computational aspect, let us find the number of $\ast$![]() and direct products. Since every supercharacter theory of $C_p$
and direct products. Since every supercharacter theory of $C_p$![]() comes from automorphisms, and two distinct subgroups of $\mathrm {Aut}(C_p)$
comes from automorphisms, and two distinct subgroups of $\mathrm {Aut}(C_p)$![]() produce two distinct supercharacter theories, we find that the number of distinct supercharacter theories of $C_p$
produce two distinct supercharacter theories, we find that the number of distinct supercharacter theories of $C_p$![]() is $\tau (p-1)$
is $\tau (p-1)$![]() , where $\tau (n)$
, where $\tau (n)$![]() is the number of divisors of the integer $n$
is the number of divisors of the integer $n$![]() . A $\ast$
. A $\ast$![]() -product of $G$
-product of $G$![]() is determined by three pieces of information: A non-trivial, proper (normal) subgroup $N$
is determined by three pieces of information: A non-trivial, proper (normal) subgroup $N$![]() , a supercharacter theory of $N$
, a supercharacter theory of $N$![]() , and a supercharacter theory of $G/N$
, and a supercharacter theory of $G/N$![]() . Since $N\cong G/N$
. Since $N\cong G/N$![]() , it follows that there are $(p+1)\tau (p-1)^{2}$
, it follows that there are $(p+1)\tau (p-1)^{2}$![]() supercharacter theories of $G=C_p\times C_p$
supercharacter theories of $G=C_p\times C_p$![]() that can be realized as a non-trivial $\ast$
that can be realized as a non-trivial $\ast$![]() -products. Note that $\mathsf {m}(G)=\mathrm {m}(H)\times \mathsf {m}(N)$
-products. Note that $\mathsf {m}(G)=\mathrm {m}(H)\times \mathsf {m}(N)$![]() for any choice of two distinct non-trivial, proper subgroups $H$
for any choice of two distinct non-trivial, proper subgroups $H$![]() and $N$
and $N$![]() . Thus, there are $1+\binom {p+1}{2}(\tau (p-1)^{2}-1)$
. Thus, there are $1+\binom {p+1}{2}(\tau (p-1)^{2}-1)$![]() supercharacter theories of $G=C_p\times C_p$
supercharacter theories of $G=C_p\times C_p$![]() that can be realized as non-trivial direct products, where we are including $\mathsf {m}(G)$
that can be realized as non-trivial direct products, where we are including $\mathsf {m}(G)$![]() .
.
To compute the supercharacter theories of $G$![]() coming from automorphisms, we constructed the natural action of $\mathrm {Aut}(G)$
coming from automorphisms, we constructed the natural action of $\mathrm {Aut}(G)$![]() on $\mathrm {Irr}(G)$
on $\mathrm {Irr}(G)$![]() , which gave us a faithful representation of $\mathrm {Aut}(G)$
, which gave us a faithful representation of $\mathrm {Aut}(G)$![]() into $\mathrm {Sym}(\mathrm {Irr}(G))$
into $\mathrm {Sym}(\mathrm {Irr}(G))$![]() . Using this permutation representation, we used MAGMA's Subgroups function to find representatives of the conjugacy classes of subgroups of $\mathrm {Aut}(G)$
. Using this permutation representation, we used MAGMA's Subgroups function to find representatives of the conjugacy classes of subgroups of $\mathrm {Aut}(G)$![]() . Finally, we expanded the classes to find all of the subgroups of $\mathrm {Aut}(G)$
. Finally, we expanded the classes to find all of the subgroups of $\mathrm {Aut}(G)$![]() and constructed the orbits of these subgroups on $\mathrm {Irr}(G)$
and constructed the orbits of these subgroups on $\mathrm {Irr}(G)$![]() .
.
Computing the total number of partition supercharacter theories of each type is an easy combinatorics exercise. The number of supernormal subgroups of $\mathsf {S}_{\mathcal {P}}$![]() is the multiplicity of 1 in the partition $\mathcal {P}$
is the multiplicity of 1 in the partition $\mathcal {P}$![]() . Suppose $\mathcal {P}$
. Suppose $\mathcal {P}$![]() has shape $1^{n_1}+2^{n_2}+\dotsb +(p+1)^{n_{p+1}}$
has shape $1^{n_1}+2^{n_2}+\dotsb +(p+1)^{n_{p+1}}$![]() . Let $m_0=0$
. Let $m_0=0$![]() and define $m_i=m_{i-1}+in_i$
and define $m_i=m_{i-1}+in_i$![]() for $i\ge 1$
for $i\ge 1$![]() . Let
. Let
Then the number of partition supercharacter theories with shape $\mathcal {P}$![]() is $\prod _{i=1}^{p+1}\mathcal {N}_i$
is $\prod _{i=1}^{p+1}\mathcal {N}_i$![]() .
.
We remind the reader that all of the product supercharacter theories are automorphic supercharacter theories. Hence, those two entries are equal for a given group if and only if all of the automorphic supercharacter theories are product supercharacter theories. Also, it is possible for a supercharacter theory to be both an automorphic supercharacter theory and a partition supercharacter theory. The overlap between these two sets explains why the total number of supercharacter theories is less that then the sum of the number of partition supercharacter theories and automorphic supercharacter theories.
If $p=2$![]() , then one can easily compute $\mathrm {SCT}(G)$
, then one can easily compute $\mathrm {SCT}(G)$![]() by hand. In fact, it would not be terribly difficult to do so for $p=3$
by hand. In fact, it would not be terribly difficult to do so for $p=3$![]() . However, we used Hendrickson's algorithm given in [Reference Hendrickson9] to compute $\mathrm {SCT}(G)$
. However, we used Hendrickson's algorithm given in [Reference Hendrickson9] to compute $\mathrm {SCT}(G)$![]() for $p=3$
for $p=3$![]() and $p=5$
and $p=5$![]() . This is unfortunately computationally infeasible for $p>5$
. This is unfortunately computationally infeasible for $p>5$![]() . The following table summarizes these findings.
. The following table summarizes these findings.

Now let $p=7$![]() or $p=11$
or $p=11$![]() . For $i$
. For $i$![]() sufficiently large, we were able to compute the total number of supercharacter theories of type $T_i$
sufficiently large, we were able to compute the total number of supercharacter theories of type $T_i$![]() . To accomplish this, we showed that every supercharacter theory of type $T_i$
. To accomplish this, we showed that every supercharacter theory of type $T_i$![]() either came from automorphisms or partitions by using the following sequence of steps.
either came from automorphisms or partitions by using the following sequence of steps.
Step 1: Suppose that $\mathsf {S}$![]() is a supercharacter theory of $G=C_p\times C_p$
is a supercharacter theory of $G=C_p\times C_p$![]() of type $T_i$
of type $T_i$![]() for $i\ge 3$
for $i\ge 3$![]() and $p\in \{7,\,11\}$
and $p\in \{7,\,11\}$![]() . Let $H$
. Let $H$![]() be an $\mathsf {S}$
be an $\mathsf {S}$![]() -normal subgroup of $G$
-normal subgroup of $G$![]() . Since we have checked Conjecture 6.4 for $G$
. Since we have checked Conjecture 6.4 for $G$![]() , we know that $\mathsf {S}_H=\mathsf {M}(H)$
, we know that $\mathsf {S}_H=\mathsf {M}(H)$![]() . Since $G$
. Since $G$![]() has at least three non-trivial, proper $\mathsf {S}$
has at least three non-trivial, proper $\mathsf {S}$![]() -normal subgroups, we also know that $\mathsf {S}_{G/H}=\mathsf {M}(G/H)$
-normal subgroups, we also know that $\mathsf {S}_{G/H}=\mathsf {M}(G/H)$![]() . Let $g$
. Let $g$![]() be an element of $G$
be an element of $G$![]() that does not lie in an $\mathsf {S}$
that does not lie in an $\mathsf {S}$![]() -normal subgroup of $G$
-normal subgroup of $G$![]() . Since $\lvert {\mathrm {cl}_{\mathsf {S}_{G/H}}(g)}\rvert=p-1$
. Since $\lvert {\mathrm {cl}_{\mathsf {S}_{G/H}}(g)}\rvert=p-1$![]() and $\lvert {\mathrm {cl}_{\mathsf {S}_{G/H}}(g)}\rvert$
and $\lvert {\mathrm {cl}_{\mathsf {S}_{G/H}}(g)}\rvert$![]() divides $\lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert$
divides $\lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert$![]() , we know that $\lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert$
, we know that $\lvert {\mathrm {cl}_{\mathsf {S}}(g)}\rvert$![]() is divisible by $p-1$
is divisible by $p-1$![]() .
.
Step 2: Let $H_1,\,\dotsc,\,H_n$![]() be the set of all non-trivial, proper $\mathsf {S}$
be the set of all non-trivial, proper $\mathsf {S}$![]() -normal subgroups of $G$
-normal subgroups of $G$![]() . Let $L=G\setminus \bigcup _{i=1}^{n}H_i$
. Let $L=G\setminus \bigcup _{i=1}^{n}H_i$![]() . Let $\mathcal {G}$
. Let $\mathcal {G}$![]() be the subset of all $P\subseteq L$
be the subset of all $P\subseteq L$![]() for which $\lvert {P}\rvert$
for which $\lvert {P}\rvert$![]() is divisible by $p-1$
is divisible by $p-1$![]() and also satisfy $\{P\}\in \mathcal {K}^{\infty }(\{P\})$
and also satisfy $\{P\}\in \mathcal {K}^{\infty }(\{P\})$![]() (Hendrickson calls subsets satisfying this latter condition good subsets).
(Hendrickson calls subsets satisfying this latter condition good subsets).
Step 3: For each $P\in \mathcal {G}$![]() , determine if $\mathcal {C}_P\subseteq \mathscr {K}^{\infty }(\mathcal {C}_P)$
, determine if $\mathcal {C}_P\subseteq \mathscr {K}^{\infty }(\mathcal {C}_P)$![]() , where $\mathcal {C}_P=\{\{1\},\,H_1\setminus \{1\},\,H_2\setminus \{1\},\,\dotsc,\,H_n\setminus \{1\},\,P\}$
, where $\mathcal {C}_P=\{\{1\},\,H_1\setminus \{1\},\,H_2\setminus \{1\},\,\dotsc,\,H_n\setminus \{1\},\,P\}$![]() . If $P$
. If $P$![]() does not satisfy this condition, then $P$
does not satisfy this condition, then $P$![]() is not an $\mathsf {S}$
is not an $\mathsf {S}$![]() -class. After completing each of the above steps, the only subsets $P$
-class. After completing each of the above steps, the only subsets $P$![]() that remained had the form $P=\bigcup _{x\in J}(\langle {x}\rangle-1)$
that remained had the form $P=\bigcup _{x\in J}(\langle {x}\rangle-1)$![]() for some subset $J\subseteq L$
for some subset $J\subseteq L$![]() . In particular, $\mathsf {S}$
. In particular, $\mathsf {S}$![]() must be a partition supercharacter theory by Proposition 6.13.
must be a partition supercharacter theory by Proposition 6.13.
In [Reference Ziv-Av25], the total number of Cayley isomorphism classes of Schur rings of the groups of order 49 is given. Moreover, they provide a GAP repository of the representatives of these classes [26] for each group up to isomorphism of order less than 64. In particular, this means we have the representatives for $G=C_7\times C_7$![]() . Recall that every Schur ring of the abelian group $G$
. Recall that every Schur ring of the abelian group $G$![]() gives the superclasses for a supercharacter theory of $G$
gives the superclasses for a supercharacter theory of $G$![]() . In the language of Schur rings, two supercharacter theories $\mathsf {S}$
. In the language of Schur rings, two supercharacter theories $\mathsf {S}$![]() and $\mathsf {T}$
and $\mathsf {T}$![]() of $G$
of $G$![]() could be called Cayley isomorphic if there is an automorphism $\sigma$
could be called Cayley isomorphic if there is an automorphism $\sigma$![]() of $G$
of $G$![]() such that $\mathrm {Cl}(\mathsf {T})=\{K^{\sigma }:K\in \mathrm {Cl}(\mathsf {S})\}$
such that $\mathrm {Cl}(\mathsf {T})=\{K^{\sigma }:K\in \mathrm {Cl}(\mathsf {S})\}$![]() . Thus, the information given in [26] provides representatives for the $\mathrm {Aut}(G)$
. Thus, the information given in [26] provides representatives for the $\mathrm {Aut}(G)$![]() -orbits on $\mathrm {SCT}(G)$
-orbits on $\mathrm {SCT}(G)$![]() . By computing the $\mathrm {Aut}(G)$
. By computing the $\mathrm {Aut}(G)$![]() -orbits of each of the representatives, we found that $G$
-orbits of each of the representatives, we found that $G$![]() has exactly 5222 supercharacter theories, which is exactly the number of supercharacter theories of $G$
has exactly 5222 supercharacter theories, which is exactly the number of supercharacter theories of $G$![]() that either come from automorphisms or partitions. Thus, we may conclude that every supercharacter theory of $G=C_7\times C_7$
that either come from automorphisms or partitions. Thus, we may conclude that every supercharacter theory of $G=C_7\times C_7$![]() either comes from automorphisms or partitions.
either comes from automorphisms or partitions.
The following table summarizes our computational results for $p=7$![]() and $p=11$
and $p=11$![]() . We indicate the information that is unavailable with a dash. The only such information is the total number of supercharacter theories of $G=C_7\times C_7$
. We indicate the information that is unavailable with a dash. The only such information is the total number of supercharacter theories of $G=C_7\times C_7$![]() of type $T_i$
of type $T_i$![]() for $0\le i\le 2$
for $0\le i\le 2$![]() and the total number of supercharacter theories of $G=C_{11}\times C_{11}$
and the total number of supercharacter theories of $G=C_{11}\times C_{11}$![]() of type $T_i$
of type $T_i$![]() for $0\le i\le 8$
for $0\le i\le 8$![]() . The top three entries of the $p=7$
. The top three entries of the $p=7$![]() case were only able to be completed with the aid of [26]; the remaining entries rely on our computations as described above.
case were only able to be completed with the aid of [26]; the remaining entries rely on our computations as described above.

Given all of the evidence presented thus far, it is feasible that one may be able to classify the supercharacter theories of $C_p\times C_p$![]() that have at least one non-trivial, proper $\mathsf {S}$
that have at least one non-trivial, proper $\mathsf {S}$![]() -normal subgroup (a supercharacter theory with no non-trivial, proper $\mathsf {S}$
-normal subgroup (a supercharacter theory with no non-trivial, proper $\mathsf {S}$![]() -normal subgroup has been referred to as simple). The others may prove much more difficult to describe. For example, if $N\lhd _{\mathsf {S}}G$
-normal subgroup has been referred to as simple). The others may prove much more difficult to describe. For example, if $N\lhd _{\mathsf {S}}G$![]() , then $\mathsf {S}\preccurlyeq \mathsf {S}_N\ast \mathsf {S}_{G/N}$
, then $\mathsf {S}\preccurlyeq \mathsf {S}_N\ast \mathsf {S}_{G/N}$![]() , which puts limitations on which elements can lie in the same $\mathsf {S}$
, which puts limitations on which elements can lie in the same $\mathsf {S}$![]() -class. Also $\lvert {\mathrm {cl}_{\mathsf {S}_{G/N}}(gN)}\rvert$
-class. Also $\lvert {\mathrm {cl}_{\mathsf {S}_{G/N}}(gN)}\rvert$![]() must divide $\lvert {\mathrm {cl}_{\mathsf {S}}(g)} \rvert$
must divide $\lvert {\mathrm {cl}_{\mathsf {S}}(g)} \rvert$![]() for every $g\in G\setminus N$
for every $g\in G\setminus N$![]() , which puts arithmetic restrictions on the possible sizes of $\mathsf {S}$
, which puts arithmetic restrictions on the possible sizes of $\mathsf {S}$![]() -classes. When $\mathsf {S}$
-classes. When $\mathsf {S}$![]() is simple though, none of these restrictions apply. However, given all that we have observed, it is possible that a classification may only involve the partition supercharacter theories and those coming from automorphisms.
is simple though, none of these restrictions apply. However, given all that we have observed, it is possible that a classification may only involve the partition supercharacter theories and those coming from automorphisms.