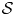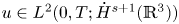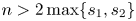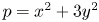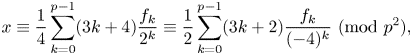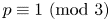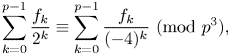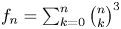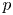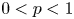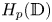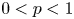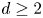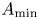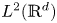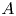Most read
This page lists the top ten most read articles for this journal based on the number of full text views and downloads recorded on Cambridge Core over the last 90 days. This list is updated on a daily basis.
Vanishing limit for the three-dimensional incompressible Phan-Thien–Tanner system
- Part of:
-
- Published online by Cambridge University Press:
- 27 March 2023, pp. 673-698
-
- Article
- Export citation
Brownian motion on the golden ratio Sierpinski gasket
- Part of:
-
- Published online by Cambridge University Press:
- 03 April 2023, pp. 699-726
-
- Article
- Export citation
Fractal dimension of potential singular points set in the Navier–Stokes equations under supercritical regularity
- Part of:
-
- Published online by Cambridge University Press:
- 18 April 2023, pp. 727-745
-
- Article
- Export citation
Spreading dynamics of a discrete Nicholson's blowflies equation with distributed delay
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2023, pp. 746-768
-
- Article
- Export citation
Minimal energy for geometrically nonlinear elastic inclusions in two dimensions
- Part of:
-
- Published online by Cambridge University Press:
- 12 May 2023, pp. 769-792
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
A Jordan–Hölder theorem for skew left braces and their applications to multipermutation solutions of the Yang–Baxter equation
- Part of:
-
- Published online by Cambridge University Press:
- 24 April 2023, pp. 793-809
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Estimates for the nonlinear viscoelastic damped wave equation on compact Lie groups
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2023, pp. 810-829
-
- Article
- Export citation
Distribution and moments of the error term in the lattice point counting problem for three-dimensional Cygan–Korányi balls
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2023, pp. 830-861
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Nonexistence of anti-symmetric solutions for fractional Hardy–Hénon system
- Part of:
-
- Published online by Cambridge University Press:
- 15 May 2023, pp. 862-886
-
- Article
- Export citation
On two congruence conjectures of Z.-W. Sun involving Franel numbers
- Part of:
-
- Published online by Cambridge University Press:
- 16 May 2023, pp. 887-905
-
- Article
- Export citation
Democracy of quasi-greedy bases in $\boldsymbol p$
 -Banach spaces with applications to the efficiency of the Thresholding Greedy Algorithm in the Hardy spaces $\boldsymbol {H_{p}({\mathbb {D}}^{d})}$
-Banach spaces with applications to the efficiency of the Thresholding Greedy Algorithm in the Hardy spaces $\boldsymbol {H_{p}({\mathbb {D}}^{d})}$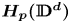
- Part of:
-
- Published online by Cambridge University Press:
- 24 May 2023, pp. 906-928
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
General kernel estimates of Schrödinger-type operators with unbounded diffusion terms
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2023, pp. 929-960
-
- Article
-
- You have access
- Open access
- HTML
- Export citation
Second-kind symmetric periodic orbits for planar perturbed Kepler problems and applications
- Part of:
-
- Published online by Cambridge University Press:
- 19 May 2023, pp. 961-992
-
- Article
- Export citation
PRM volume 154 issue 3 Cover and Front matter
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. f1-f2
-
- Article
-
- You have access
- Export citation
PRM volume 154 issue 3 Cover and Back matter
-
- Published online by Cambridge University Press:
- 16 May 2024, pp. b1-b2
-
- Article
-
- You have access
- Export citation