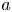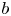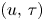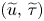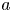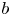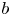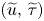1. Introduction
In this paper, we are interested in only homogeneous flow of incompressible isothermal polymer fluids. The Phan-Thien–Tanner (PTT) model originates from the works of Nhan Phan-Thien and Roger I. Tanner in [Reference Phan-Thien44, Reference Phan-Thien and Tanner45]. This model attempts to describe the behaviour of this complex mixture of polymers and fluids, and as such, it presents numerous challenges, simultaneously at the level of their derivation, that of their numerical simulation and mathematical treatment. This flow is governed by the following continuity and momentum balance equations:
where $u$![]() , $p$
, $p$![]() and $T$
and $T$![]() represent the velocity field, the isotropic pressure and the stress tensor, respectively. The stress tensor $T$
represent the velocity field, the isotropic pressure and the stress tensor, respectively. The stress tensor $T$![]() , corresponding to the rates of creation and destruction of junctions which depend on the instantaneous elastic energy of the network, or equivalently, the average extension of the network strand, is often divided into the following two parts:
, corresponding to the rates of creation and destruction of junctions which depend on the instantaneous elastic energy of the network, or equivalently, the average extension of the network strand, is often divided into the following two parts:
where $\tau$![]() is the polymers contribution to the stress tensor and $D(u):=(1/2) (\nabla u+(\nabla u)^T)$
is the polymers contribution to the stress tensor and $D(u):=(1/2) (\nabla u+(\nabla u)^T)$![]() . Two constants $\mu _1>0$
. Two constants $\mu _1>0$![]() and $\mu >0$
and $\mu >0$![]() are the elastic coefficient and the solvent viscosity coefficient, respectively.
are the elastic coefficient and the solvent viscosity coefficient, respectively.
Throughout this paper, we shall focus on the linear PTT model, which is a well-studied phenomenological constitutive model for polymers. One can deduce that
and the ‘objective derivative’ ${\mathcal {D} \tau }/{\mathcal {D} t}$![]() is denoted as follows:
is denoted as follows:
where $\Omega (u):=(1/2)(\nabla u-(\nabla u)^T)$![]() , $\lambda _1>0$
, $\lambda _1>0$![]() is the relaxation time of the fluids, $\lambda _2$
is the relaxation time of the fluids, $\lambda _2$![]() $(0 \leq \lambda _2 <\lambda _1)$
$(0 \leq \lambda _2 <\lambda _1)$![]() is the retardation time of the fluids, $\eta >0$
is the retardation time of the fluids, $\eta >0$![]() is the polymer viscosity coefficient, $\varepsilon$
is the polymer viscosity coefficient, $\varepsilon$![]() is a parameter controlling the elongational viscosity coefficient and $\lambda$
is a parameter controlling the elongational viscosity coefficient and $\lambda$![]() is a constant that is typically in $[-1,\,1]$
is a constant that is typically in $[-1,\,1]$![]() . In particular, we call the system a co-rotational case when $\lambda =0$
. In particular, we call the system a co-rotational case when $\lambda =0$![]() .
.
For the sake of conciseness, we set $a={1}/{\lambda _{1}}$![]() , $b={\varepsilon }/{\eta }$
, $b={\varepsilon }/{\eta }$![]() and $\mu _2=({2\eta }/{\lambda _{1}}) (1-{\lambda _{2}}/{\lambda _{1}})$
and $\mu _2=({2\eta }/{\lambda _{1}}) (1-{\lambda _{2}}/{\lambda _{1}})$![]() . Two constants $a>0$
. Two constants $a>0$![]() and $\mu _2>0$
and $\mu _2>0$![]() are associated with the Deborah number $De={\mu _2}/{a}$
are associated with the Deborah number $De={\mu _2}/{a}$![]() , which indicates the relation between the characteristic flow time and the elastic time (see [Reference Bird, Armstrong and Hassager4]). The constant $b\geq 0$
, which indicates the relation between the characteristic flow time and the elastic time (see [Reference Bird, Armstrong and Hassager4]). The constant $b\geq 0$![]() is related to the rates of creation and destruction for the polymeric network junctions. Using the notations introduced above, we aim to solve the following three-dimensional incompressible PTT system:
is related to the rates of creation and destruction for the polymeric network junctions. Using the notations introduced above, we aim to solve the following three-dimensional incompressible PTT system:

Here, $Q(\tau,\,\nabla u)$![]() is a given bilinear form
is a given bilinear form
It can be seen that the PTT system is derived from the coupling of the constitutive equation with the incompressible Navier–Stokes equations. The coupling in Navier–Stokes equations comes from an extra stress tensor contributed from the polymers. Without taking into account the rates of creation and destruction for the polymeric network junctions (i.e. $a>0$![]() and $b=0$
and $b=0$![]() ), then the second equation of system (PTT) is replaced by
), then the second equation of system (PTT) is replaced by
One reduces to the well-known Oldroyd-B system, which models the motion of some simple types of steady flow of certain idealized elastico-viscous liquids (see [Reference Oldroyd42]). Note that there is a new nonlinear term $b({\rm tr}\,\tau )\tau$![]() in the constitutive equation of system (PTT), which is a big difference from the Oldroyd-B system. The limit system as $(a,\,b)\rightarrow (0,\,0)$
in the constitutive equation of system (PTT), which is a big difference from the Oldroyd-B system. The limit system as $(a,\,b)\rightarrow (0,\,0)$![]() formally becomes the following three-dimensional incompressible Oldroyd-B system without damping mechanism:
formally becomes the following three-dimensional incompressible Oldroyd-B system without damping mechanism:

The main objective of this paper is to show the relation of the PTT system to the Oldroyd-B system (with or without damping mechanism). Until now, this question actually remains open. In the sequence, we will give an overview on the study for the PTT and Oldroyd-type models.
To begin, we review some mathematical works dedicated to the PTT model. To the best of our knowledge, it is universally known that the PTT model has been widely studied in numerical analysis (see [Reference Bautista, Sánchez, Arcos and Méndez2, Reference Garduño, Tamaddon-Jahromi, Walters and Webster16, Reference Oliveira and Pinho43]). The first mathematical work devoted to the PTT system is by Masmoudi [Reference Masmoudi41]. There, the global existence of weak solutions was proven. Recently, Chen et al. [Reference Chen, Luo and Yao8] proved the global existence of strong solutions for the periodic PTT system without damping mechanism (i.e. $a=0$![]() and $b\geq 0$
and $b\geq 0$![]() ). In a more general context, the global well-posedness of the Cauchy problem for the linear and generalized PTT systems in the whole space was achieved by Chen et al. [Reference Chen, Li, Yao and an Yao6, Reference Chen, Luo and Zhai9] in the critical Besov spaces and [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao10] in Sobolev spaces. In this paper, we would like to study in a sequel the limit process of the PTT system with $0\leq b\leq Ca$
). In a more general context, the global well-posedness of the Cauchy problem for the linear and generalized PTT systems in the whole space was achieved by Chen et al. [Reference Chen, Li, Yao and an Yao6, Reference Chen, Luo and Zhai9] in the critical Besov spaces and [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao10] in Sobolev spaces. In this paper, we would like to study in a sequel the limit process of the PTT system with $0\leq b\leq Ca$![]() when coefficients $a$
when coefficients $a$![]() and $b$
and $b$![]() go to $0$
go to $0$![]() simultaneously (or, only $b$
simultaneously (or, only $b$![]() goes to $0$
goes to $0$![]() ) and aim to prove in particular that the obtained limit is the solution of the corresponding Oldroyd-B system.
) and aim to prove in particular that the obtained limit is the solution of the corresponding Oldroyd-B system.
We also review some mathematical works dedicated to the Oldroyd-type models. For all we know, the related Oldroyd-type models have been analysed extensively since 1990. The main breakthrough of the Oldroyd-B system was made by Guillopé and Saut [Reference Guillopé and Saut17, Reference Guillopé and Saut18]. In the above studies, they proved the local existence of strong solutions and the global existence of one-dimensional shear flows. In the multi-dimensional case, the local well-posedness in Sobolev spaces was first proven by Fernández-Cara et al. [Reference Fernández-Cara, Guillén and Ortega15]. Later, Chemin and Masmoudi [Reference Chemin and Masmoudi5] not only proved the local well-posedness in the critical Besov spaces, but gave a low bound for the lifespan as well. Then, Feng et al. and Lei et al. gave some blow up criteria in [Reference Feng, Zhu and Zi14, Reference Lei, Masmoudi and Zhou31]. In [Reference Lions and Masmoudi39], the global existence of weak solutions for general initial data in the co-rotational system was studied by Lions and Masmoudi. In regard to strong solutions, the global existence for small smooth perturbations of a stable equilibrium was first presented in [Reference Lin, Liu and Zhang36]. Surprisingly, there are a number of studies concerning the global existence of strong solutions of the Cauchy problem with small initial data by using different methods, for example, see [Reference Chen and Zhang11, Reference Lei, Liu and Zhou32, Reference Lei and Zhou33, Reference Lin, Liu and Zhang36, Reference Zhang and Fang52, Reference Zhu54] and the references cited therein. In particular, the global existence for the Oldroyd-B system without damping mechanism was discussed in [Reference Zhu54]. We should mention here that He and Xu [Reference He and Xu19], Lin and Zhang [Reference Lin and Zhang37] and Sun and Zhang [Reference Sun and Zhang48] have obtained similar results involving the initial-boundary problem of the incompressible viscoelastic fluid models. For a class of large initial data, Fang and Zi [Reference Fang and Zi13] and Jiang and Jiang [Reference Jiang and Jiang24] made some contributions to the global existence of strong solutions. The optimal time decay estimates have been established recently in [Reference Hieber, Wen and Zi20] for the incompressible Oldroyd-B system and similar results in [Reference Wang and Wen50] for the compressible case. For more results concerning the related compressible viscoelastic fluids models, one may refer to [Reference Barrett, Lu and Süli1, Reference Hu and Wang22, Reference Hu and Wu23, Reference Lu and Zhang40, Reference Qian and Zhang46, Reference Zhou, Zhu and Zi53]. It has been shown that the weak solutions and strong solutions exist globally in time.
In addition, we recall some results related to the limit problems. There has been much progress on the limit problems of various flow models in the last few decades, especially on incompressible limit. The mathematical studies of incompressible limit were stated in [Reference Klainerman and Majda28, Reference Lions and Masmoudi38] for Navier–Stokes equations and in [Reference Hu and Wang21, Reference Jiang, Ju and Li25] for magnetohydrodynamic equations. As for the Oldroyd-B system, incompressible limit problem was investigated in [Reference Lei30, Reference Lei and Zhou33]. Besides, Ju et al. investigated the quasineutral limit for the compressible Navier–Stokes–Poisson equations (for both isentropic and non-isentropic cases) in [Reference Ju, Li and Li26, Reference Ju, Li and Wang27]. As in the previous works, the existence of global classical (or weak) solutions for the incompressible case was shown via incompressible limit. More results on the other limit problems of various flow models may be found in [Reference Bian, Yao and Zhu3, Reference Chen and Zhai12, Reference Lai, Wen and Yao29, Reference Li and Titi34, Reference Li and Zhu35, Reference Wang, Wang and Zhang49, Reference Yao, Zhu and Zi51]. Heuristically, we hope that the process of the vanishing limit for the PTT system selects a physical relevant solution of the corresponding Oldroyd-B system.
In this paper, we aim to establish the vanishing limit of the PTT system for incompressible fluids. Let $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , under the smallness assumptions on the initial data, our first aim is to prove the global existence of strong solutions for the PTT system with the a priori estimates, uniformly with respect to time $t$
, under the smallness assumptions on the initial data, our first aim is to prove the global existence of strong solutions for the PTT system with the a priori estimates, uniformly with respect to time $t$![]() and coefficients $a$
and coefficients $a$![]() and $b$
and $b$![]() . Our second purpose is to prove the global existence for the limit system via the vanishing limit. Taking advantage of the uniform energy and decay estimates stated earlier, it is possible to pass to the limit when $a$
. Our second purpose is to prove the global existence for the limit system via the vanishing limit. Taking advantage of the uniform energy and decay estimates stated earlier, it is possible to pass to the limit when $a$![]() and $b$
and $b$![]() go to 0 simultaneously (or, only $b$
go to 0 simultaneously (or, only $b$![]() goes to $0$
goes to $0$![]() ). This result justifies that the limit is indeed a strong solution of the corresponding Oldroyd-B system and has the required regularity. In addition, we investigate the rate of convergence of the PTT system towards the corresponding Oldroyd-B system for solutions having the above regularity. We shall see that the rate strongly depends on time $t$
). This result justifies that the limit is indeed a strong solution of the corresponding Oldroyd-B system and has the required regularity. In addition, we investigate the rate of convergence of the PTT system towards the corresponding Oldroyd-B system for solutions having the above regularity. We shall see that the rate strongly depends on time $t$![]() and coefficients $a$
and coefficients $a$![]() and $b$
and $b$![]() . Moreover, we prove the local a priori estimates in large norm. A similar result holds true for some time interval $[0,\,T]$
. Moreover, we prove the local a priori estimates in large norm. A similar result holds true for some time interval $[0,\,T]$![]() . As a consequence, this is the first paper devoted to establishing a relation between the PTT system and the Oldroyd-B system with or without damping mechanism.
. As a consequence, this is the first paper devoted to establishing a relation between the PTT system and the Oldroyd-B system with or without damping mechanism.
Notation: We shall introduce some notations. Unless otherwise indicated, we omit $\mathbb {R}^3$![]() in the rest of the proof. For the sake of simplicity, we restrict our attention here to the case where $\mu =\mu _1=\mu _2=1$
in the rest of the proof. For the sake of simplicity, we restrict our attention here to the case where $\mu =\mu _1=\mu _2=1$![]() . Throughout this paper, $C$
. Throughout this paper, $C$![]() denotes a generic positive constant independent of $t$
denotes a generic positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() .
.
We can now describe our main results. We first state the following theorem, the global well-posedness for system (PTT) with small initial data. In passing, we will establish suitable a priori estimates, uniformly in both time $t$![]() and coefficients $a$
and coefficients $a$![]() and $b$
and $b$![]() .
.
Theorem 1.1 Let $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() . Assume that the initial data $(u_0,\,\tau _0)$
. Assume that the initial data $(u_0,\,\tau _0)$![]() satisfies $\mathop {\rm div}\nolimits u_0=0$
satisfies $\mathop {\rm div}\nolimits u_0=0$![]() , $(\tau _0)_{ij}=(\tau _0)_{ji}$
, $(\tau _0)_{ij}=(\tau _0)_{ji}$![]() and $({|\nabla |^{-1}} u_0,\,{|\nabla |^{-1}}\tau _0)\in H^3(\mathbb {R}^3)$
and $({|\nabla |^{-1}} u_0,\,{|\nabla |^{-1}}\tau _0)\in H^3(\mathbb {R}^3)$![]() . There exists a sufficiently small positive constant $\delta _0$
. There exists a sufficiently small positive constant $\delta _0$![]() , such that if
, such that if
then the problem (PTT) admits a unique global classical solution $(u,\, \tau )$![]() , which satisfies
, which satisfies

where $C_1$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() . Moreover, the following time decay estimates hold true$:$
. Moreover, the following time decay estimates hold true$:$![]()

Remark 1.2 We should mention that the assumption $0\leq a\leq 1$![]() of theorem 1.1 is reasonable. In this paper, one of the questions to consider is the vanishing limit for system (PTT) when $a$
of theorem 1.1 is reasonable. In this paper, one of the questions to consider is the vanishing limit for system (PTT) when $a$![]() tends to zero, so here we assume that $0\leq a\leq 1$
tends to zero, so here we assume that $0\leq a\leq 1$![]() . The results of the case $a=0$
. The results of the case $a=0$![]() were proven in some earlier works, see [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao8, Reference Chen, Luo and Yao10, Reference Zhu54] for more details.
were proven in some earlier works, see [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao8, Reference Chen, Luo and Yao10, Reference Zhu54] for more details.
Remark 1.3 We should also point out that $0\leq b\leq Ca$![]() is a reasonable technical assumption for our limiting problem. In the case $a = 0$
is a reasonable technical assumption for our limiting problem. In the case $a = 0$![]() and $b>0$
and $b>0$![]() , we see that the solution of system (PTT) will blow up in finite time if the initial data ${\rm tr}\,\tau _0(x) <0$
, we see that the solution of system (PTT) will blow up in finite time if the initial data ${\rm tr}\,\tau _0(x) <0$![]() , which have been discussed in [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao8, Reference Chen, Luo and Yao10]. Indeed, the authors in [Reference Chen, Luo and Yao8] only have to consider the initial data ${\rm tr}\,\tau _0(x)>0$
, which have been discussed in [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao8, Reference Chen, Luo and Yao10]. Indeed, the authors in [Reference Chen, Luo and Yao8] only have to consider the initial data ${\rm tr}\,\tau _0(x)>0$![]() in the periodic domain $\mathbb {T}^3$
in the periodic domain $\mathbb {T}^3$![]() . If we assume that $\tau _0 \in H^s({\mathbb {R}}^3)$
. If we assume that $\tau _0 \in H^s({\mathbb {R}}^3)$![]() , then $\mathop {\lim }\nolimits _{x\rightarrow +\infty } \tau _0(x)=0$
, then $\mathop {\lim }\nolimits _{x\rightarrow +\infty } \tau _0(x)=0$![]() which contracts to ${\rm tr}\, \tau _0(x)>0$
which contracts to ${\rm tr}\, \tau _0(x)>0$![]() . Moreover, under the assumption that ${\rm tr}\, \tau _0(x)>0$
. Moreover, under the assumption that ${\rm tr}\, \tau _0(x)>0$![]() , the authors in [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao10] obtained the global existence of strong solutions provided that the initial data are close to a nontrivial particular solution (depending only on $t$
, the authors in [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao10] obtained the global existence of strong solutions provided that the initial data are close to a nontrivial particular solution (depending only on $t$![]() ) in the whole space $\mathbb {R}^3$
) in the whole space $\mathbb {R}^3$![]() . It makes no sense to consider the global well-posedness for system (PTT) with small initial data $({|\nabla |^{-1}} u_0,\,{|\nabla |^{-1}}\tau _0)\in H^3(\mathbb {R}^3)$
. It makes no sense to consider the global well-posedness for system (PTT) with small initial data $({|\nabla |^{-1}} u_0,\,{|\nabla |^{-1}}\tau _0)\in H^3(\mathbb {R}^3)$![]() in the case $a = 0$
in the case $a = 0$![]() and $b>0$
and $b>0$![]() .
.
Remark 1.4 Compared with [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao10, Reference Zhu54], here our eventual goal is to prove the convergence of the solution $(u,\,\tau )$![]() to system (PTT) with $0\leq b\leq Ca$
to system (PTT) with $0\leq b\leq Ca$![]() when coefficients $a$
when coefficients $a$![]() and $b$
and $b$![]() tend to zero simultaneously (or, only $b$
tend to zero simultaneously (or, only $b$![]() tends to zero). To prove this, we shall establish the uniform estimates for system (PTT) with respect to $t$
tends to zero). To prove this, we shall establish the uniform estimates for system (PTT) with respect to $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() .
.
Remark 1.5 Actually, besides the assumptions of theorem 1.1, we assume that $(u_0,\,\tau _0)\in L^1(\mathbb {R}^3)$![]() . For any fixed constant coefficients $a\geq 0$
. For any fixed constant coefficients $a\geq 0$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , we deduce not only that there exists a unique global classical solution $(u,\,\tau )$
, we deduce not only that there exists a unique global classical solution $(u,\,\tau )$![]() , but that the following time decay estimates hold true:
, but that the following time decay estimates hold true:
where $C_1$![]() is a positive constant which does not depend on $t$
is a positive constant which does not depend on $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() . This conclusion may be proved by using standard energy method, the proof of which is similar to that of this paper. We omit the details, since this is not what we focus on in this paper.
. This conclusion may be proved by using standard energy method, the proof of which is similar to that of this paper. We omit the details, since this is not what we focus on in this paper.
Remark 1.6 Furthermore, if we also assume that $(u_0,\,\tau _0)\in L^1(\mathbb {R}^3)$![]() . For any fixed constant coefficients $a>0$
. For any fixed constant coefficients $a>0$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , we can infer that the following optimal time decay estimates, for $k=0,\,1,\,2$
, we can infer that the following optimal time decay estimates, for $k=0,\,1,\,2$![]() :
:
where $C_2$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , but may depend on $a$
, but may depend on $a$![]() and $b$
and $b$![]() . The proof is similar to that of the work in [Reference Hieber, Wen and Zi20].
. The proof is similar to that of the work in [Reference Hieber, Wen and Zi20].
We are concerned with the vanishing limit for system (PTT) in the sequel. According to theorem 1.1, we shall prove the convergence of the solution $(u,\,\tau )$![]() to system (PTT) with $0\leq b\leq Ca$
to system (PTT) with $0\leq b\leq Ca$![]() when $(a,\,b)$
when $(a,\,b)$![]() tends to $(0,\,0)$
tends to $(0,\,0)$![]() . The aim is to show that when $(a,\,b)$
. The aim is to show that when $(a,\,b)$![]() tends to $(0,\,0)$
tends to $(0,\,0)$![]() , the global solution $(u,\,\tau )$
, the global solution $(u,\,\tau )$![]() of system (PTT) with $0\leq b\leq Ca$
of system (PTT) with $0\leq b\leq Ca$![]() converges to some limit solution $(\widetilde {u},\,\widetilde {\tau })$
converges to some limit solution $(\widetilde {u},\,\widetilde {\tau })$![]() , which is a global solution of system (OB).
, which is a global solution of system (OB).
Theorem 1.7 For any $T>0$![]() , let $(u,\,\tau )$
, let $(u,\,\tau )$![]() be a strong solution of system (PTT) in the time interval $[0,\,T]$
be a strong solution of system (PTT) in the time interval $[0,\,T]$![]() given by theorem 1.1. Then there exists $(\widetilde {u},\,\widetilde {\tau })$
given by theorem 1.1. Then there exists $(\widetilde {u},\,\widetilde {\tau })$![]() such that for $0\leq b\leq Ca$
such that for $0\leq b\leq Ca$![]() , if $(a,\,b)\rightarrow (0,\,0)$
, if $(a,\,b)\rightarrow (0,\,0)$![]() , it holds true for any $s \in (0,\,1/2)$
, it holds true for any $s \in (0,\,1/2)$![]() ,
,

Moreover, $(\widetilde {u},\,\widetilde {\tau })$![]() is a strong solution of system (OB) in the time interval $[0,\,T]$
is a strong solution of system (OB) in the time interval $[0,\,T]$![]() , and satisfies
, and satisfies

In addition, there exists a positive constant $C_1$![]() , independent of $t$
, independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , such that
, such that
Finally, we investigate the rate of convergence of system (PTT) towards system (OB) for solutions having the above regularity. We shall see that the rate strongly depends on $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() .
.
Theorem 1.8 Let $(u,\,\tau )$![]() be a strong solution of system (PTT) given by theorem 1.1 and $(\widetilde {u},\,\widetilde {\tau })$
be a strong solution of system (PTT) given by theorem 1.1 and $(\widetilde {u},\,\widetilde {\tau })$![]() be a strong solution of system (OB) given by theorem 1.7. Then there exists a positive constant $C_1$
be a strong solution of system (OB) given by theorem 1.7. Then there exists a positive constant $C_1$![]() , independent of $t$
, independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , such that
, such that
Remark 1.9 On the one hand, there is no derivative in the additional term $b({\rm tr}\,\tau )\tau$![]() of system (PTT), in contrast to the Oldroyd-B system. Then the proof of local well-posedness for system (PTT) is similar to that of the Oldroyd-B system. For any fixed constant coefficients $0\leq a\leq 1$
of system (PTT), in contrast to the Oldroyd-B system. Then the proof of local well-posedness for system (PTT) is similar to that of the Oldroyd-B system. For any fixed constant coefficients $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , let $(u,\,\tau )$
, let $(u,\,\tau )$![]() be a local solution of system (PTT) in the time interval $[0,\,T]$
be a local solution of system (PTT) in the time interval $[0,\,T]$![]() with the general initial data, there exists $(\widetilde {u},\,\widetilde {\tau })$
with the general initial data, there exists $(\widetilde {u},\,\widetilde {\tau })$![]() be a local solution of system (OB) in the time interval $[0,\,T]$
be a local solution of system (OB) in the time interval $[0,\,T]$![]() if $(a,\,b)\rightarrow (0,\,0)$
if $(a,\,b)\rightarrow (0,\,0)$![]() . Further, then there exist some $T>0$
. Further, then there exist some $T>0$![]() and a positive constant $\widetilde C_1$
and a positive constant $\widetilde C_1$![]() , independent of $a$
, independent of $a$![]() and $b$
and $b$![]() , but may depend on $T$
, but may depend on $T$![]() , such that for any $0\leq t\leq T$
, such that for any $0\leq t\leq T$![]() , we have
, we have
The proof of the above estimate may be obtained by arguing as in theorem 1.8, which will not be explained in detail in this paper. In fact, it turns out to be a simpler problem.
Remark 1.10 We notice that the PTT system reduces to the well-known Oldroyd-B system when $b=0$![]() . It goes without saying that similar results may be obtained for $a>0$
. It goes without saying that similar results may be obtained for $a>0$![]() and only set $b\rightarrow 0$
and only set $b\rightarrow 0$![]() . It is more of a physical significance with damping term no matter whether it is the PTT system or the Oldroyd-B system. In addition, we may get a better rate of convergence, the proof of which is actually quite similar to that of theorems 1.1, 1.7 and 1.8, because the nonlinear term $b({\rm tr}\,\tau )\tau$
. It is more of a physical significance with damping term no matter whether it is the PTT system or the Oldroyd-B system. In addition, we may get a better rate of convergence, the proof of which is actually quite similar to that of theorems 1.1, 1.7 and 1.8, because the nonlinear term $b({\rm tr}\,\tau )\tau$![]() of the PTT system can be controlled by the damping term $a\tau$
of the PTT system can be controlled by the damping term $a\tau$![]() .
.
In the last part of this section, we present the main ideas of the proofs of theorems 1.1, 1.7 and 1.8. From the point of view of the limit system (OB), it will be difficult to establish the a priori estimates, uniformly in both time $t$![]() and coefficients $a$
and coefficients $a$![]() and $b$
and $b$![]() , because system (OB) (i.e. $a=0$
, because system (OB) (i.e. $a=0$![]() and $b=0$
and $b=0$![]() ) loses damping influence about $\tau$
) loses damping influence about $\tau$![]() . In order to overcome this difficulty, motivated by the result presented in [Reference Zhu54], we study the following linearized system:
. In order to overcome this difficulty, motivated by the result presented in [Reference Zhu54], we study the following linearized system:
where $\mathbb {P}:=\mathbb {I}-\triangle ^{-1}\nabla \mathop {\rm div}\nolimits$![]() is the Leray projection operator. We decouple the linearized system and find that both $u$
is the Leray projection operator. We decouple the linearized system and find that both $u$![]() and $\mathbb {P} \mathop {\rm div}\nolimits \tau$
and $\mathbb {P} \mathop {\rm div}\nolimits \tau$![]() satisfy the following damped wave equation:
satisfy the following damped wave equation:
Therefore, we could obtain the time decay estimates of $u$![]() and $\mathbb {P} \mathop {\rm div}\nolimits \tau$
and $\mathbb {P} \mathop {\rm div}\nolimits \tau$![]() , which are useful to deal with the nonlinear terms.
, which are useful to deal with the nonlinear terms.
More specifically, the standard energy method be performed in system (PTT) then gives a bound on
Due to the presence of coefficient $a$![]() in the dissipative term for $\tau$
in the dissipative term for $\tau$![]() , the standard energy estimates above alone is not enough to prove the global-in-time estimates, uniformly in coefficients $a$
, the standard energy estimates above alone is not enough to prove the global-in-time estimates, uniformly in coefficients $a$![]() and $b$
and $b$![]() . Indeed, the nonlinear terms $u\cdot \nabla u$
. Indeed, the nonlinear terms $u\cdot \nabla u$![]() , $u\cdot \nabla \tau$
, $u\cdot \nabla \tau$![]() , $Q(\tau,\,\nabla u)$
, $Q(\tau,\,\nabla u)$![]() and $b({\rm tr}\,\tau )\tau$
and $b({\rm tr}\,\tau )\tau$![]() cannot be dealt with here. For this, we use the equation for $u$
cannot be dealt with here. For this, we use the equation for $u$![]() in system (PTT) to get the dissipation estimate for $\mathbb {P}\mathop {\rm div}\nolimits \tau$
in system (PTT) to get the dissipation estimate for $\mathbb {P}\mathop {\rm div}\nolimits \tau$![]() . In fact, due to the loss of the dissipation estimate for $\tau$
. In fact, due to the loss of the dissipation estimate for $\tau$![]() , we will establish the time decay estimates of $u$
, we will establish the time decay estimates of $u$![]() and $\mathbb {P} \mathop {\rm div}\nolimits \tau$
and $\mathbb {P} \mathop {\rm div}\nolimits \tau$![]() to deal with the nonlinear terms $u\cdot \nabla u$
to deal with the nonlinear terms $u\cdot \nabla u$![]() , $u\cdot \nabla \tau$
, $u\cdot \nabla \tau$![]() and $Q(\tau,\,\nabla u)$
and $Q(\tau,\,\nabla u)$![]() . It suffices to prove a bound on
. It suffices to prove a bound on

Note that, however, it does not seem possible to handle the nonlinear term $b({\rm tr}\,\tau )\tau$![]() . This is another difficult task. To achieve this, we may use a method as in [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao8, Reference Chen, Luo and Yao10]. We shall make full use of the structure of the constitutive equation of system (PTT) to obtain the time decay estimate of the unknown good quantity ${\rm tr}\,\tau$
. This is another difficult task. To achieve this, we may use a method as in [Reference Chen, Li, Yao and Yao7, Reference Chen, Luo and Yao8, Reference Chen, Luo and Yao10]. We shall make full use of the structure of the constitutive equation of system (PTT) to obtain the time decay estimate of the unknown good quantity ${\rm tr}\,\tau$![]() . As a consequence, we prove the global-in-time estimates for system (PTT) with small initial data, uniformly in coefficients $a$
. As a consequence, we prove the global-in-time estimates for system (PTT) with small initial data, uniformly in coefficients $a$![]() and $b$
and $b$![]() (see theorem 1.1). Moreover, we prove the convergence of the global solution $(u,\,\tau )$
(see theorem 1.1). Moreover, we prove the convergence of the global solution $(u,\,\tau )$![]() to system (PTT) with $0\leq b\leq Ca$
to system (PTT) with $0\leq b\leq Ca$![]() when $(a,\,b)\rightarrow (0,\,0)$
when $(a,\,b)\rightarrow (0,\,0)$![]() , and the global solution $(\widetilde {u},\,\widetilde {\tau })$
, and the global solution $(\widetilde {u},\,\widetilde {\tau })$![]() is obtained by passing to the limit. Hence, $(\widetilde {u},\,\widetilde {\tau })$
is obtained by passing to the limit. Hence, $(\widetilde {u},\,\widetilde {\tau })$![]() be a global solution of system (OB) (see theorem 1.7). In addition, a rate of convergence involving explicit norms will be obtained by using energy estimate (see theorem 1.8). On the one hand, according to the local well-posedness for the PTT system with general initial data, we also obtain the similar results (see remark 1.9). We mention in passing that in the case $a>0$
be a global solution of system (OB) (see theorem 1.7). In addition, a rate of convergence involving explicit norms will be obtained by using energy estimate (see theorem 1.8). On the one hand, according to the local well-posedness for the PTT system with general initial data, we also obtain the similar results (see remark 1.9). We mention in passing that in the case $a>0$![]() and only set $b\rightarrow 0$
and only set $b\rightarrow 0$![]() , similar results are also true (see remark 1.10).
, similar results are also true (see remark 1.10).
The rest of this paper is arranged as follows. In §2, we recall a few basic lemmas. Section 3 is devoted to proving the suitable a priori estimates for the PTT system, which will be useful for proving our main results. The proofs of theorems 1.1, 1.7 and 1.8 are presented in § 4.
2. Preliminary
In this section, we recall some very basic facts. The first lemma has been proven in [Reference Chen, Luo and Yao8, Reference Zhu54]; the details of the proof are omitted.
Lemma 2.1 [Reference Chen, Luo and Yao8, Reference Zhu54]
For any smooth tensor field $[\tau _{ij}]_{3\times 3}$![]() and three-dimensional vector field $u$
and three-dimensional vector field $u$![]() , it always holds that
, it always holds that

where
We introduce the following so-called Aubin–Lions lemma, which will be useful for proving theorem 1.7.
Lemma 2.2 [Reference Simon47]
Assume that $X\subset Y\subset Z$![]() are Banach spaces and $X\subset \subset Y$
are Banach spaces and $X\subset \subset Y$![]() , then the following embeddings are compact:
, then the following embeddings are compact:

3. ${A priori}$ estimates
estimates
In this section, we want to send $(a,\,b)$![]() to $(0,\,0)$
to $(0,\,0)$![]() in system (PTT) with $0\leq a\leq 1$
in system (PTT) with $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() . For this, we shall need some uniform estimates for smooth solutions with respect to $a$
. For this, we shall need some uniform estimates for smooth solutions with respect to $a$![]() and $b$
and $b$![]() . Before going into further detail, we give some basic energies and time-weighted energies as follows:
. Before going into further detail, we give some basic energies and time-weighted energies as follows:

We begin by proving the a priori estimates for smooth solutions. The following proposition 3.1 is useful for proving the existence theorem (see theorem 1.1). There, the positive constant $C^*$![]() that we obtained below does not depend on $t$
that we obtained below does not depend on $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , so that we may pass to the limit in system (PTT) with $0\leq b\leq Ca$
, so that we may pass to the limit in system (PTT) with $0\leq b\leq Ca$![]() when $(a,\,b)$
when $(a,\,b)$![]() goes to $(0,\,0)$
goes to $(0,\,0)$![]() , which then allows us to get a solution of system (OB) (see theorem 1.7). Moreover, a rate of convergence involving explicit norms will be obtained (see theorem 1.8).
, which then allows us to get a solution of system (OB) (see theorem 1.7). Moreover, a rate of convergence involving explicit norms will be obtained (see theorem 1.8).
Proposition 3.1 Suppose that $(u,\,\tau )$![]() is a solution of system (PTT) in the time interval $[0,\,T]$
is a solution of system (PTT) in the time interval $[0,\,T]$![]() and satisfies the assumptions of theorem 1.1. There exists a positive constant $\delta _0$
and satisfies the assumptions of theorem 1.1. There exists a positive constant $\delta _0$![]() , such that if
, such that if
then
where $C^{*}$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() .
.
3.1 Estimate of $\mathcal {E}_1(t)$
First of all, we shall prove the following standard energy estimates.
Lemma 3.2 Under the assumptions of proposition 3.1, it holds that
where $C$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , and
, and

Proof. Applying the operator ${|\nabla |^{-1}}\nabla ^{k}$![]() $(k=0,\,1,\,2,\,3)$
$(k=0,\,1,\,2,\,3)$![]() to system (PTT), and taking the $L^2$
to system (PTT), and taking the $L^2$![]() inner product with ${|\nabla |^{-1}}\nabla ^{k} u$
inner product with ${|\nabla |^{-1}}\nabla ^{k} u$![]() and ${|\nabla |^{-1}}\nabla ^{k}\tau$
and ${|\nabla |^{-1}}\nabla ^{k}\tau$![]() , respectively, we find that
, respectively, we find that

According to $\mathop {\rm div}\nolimits u=0$![]() and $\tau _{ij}=\tau _{ji}$
and $\tau _{ij}=\tau _{ji}$![]() , and integrating by parts in the first term, we get $I_{1}=0$
, and integrating by parts in the first term, we get $I_{1}=0$![]() . Using the facts that $\mathop {\rm div}\nolimits u=0$
. Using the facts that $\mathop {\rm div}\nolimits u=0$![]() , $\tau _{ij}=\tau _{ji}$
, $\tau _{ij}=\tau _{ji}$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , and integrating by parts, we deduce that
, and integrating by parts, we deduce that

To deal with the last term $I_4$![]() , we use Hölder's inequality to get
, we use Hölder's inequality to get

which in the last inequality we have used for the fact that

Integrating (3.4) with respect to $t$![]() , and plugging the above inequalities into the resulting inequality, we get the desired inequality (3.2).
, and plugging the above inequalities into the resulting inequality, we get the desired inequality (3.2).
Next, we aim to recover the dissipation estimate for $\mathbb {P}\mathop {\rm div}\nolimits \tau$![]() .
.
Lemma 3.3 Under the assumptions of proposition 3.1, it holds that
where $C$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , and
, and

Proof. Applying the operator ${|\nabla |^{-1}}\nabla ^k\mathbb {P}$![]() $(k=0,\,1,\,2)$
$(k=0,\,1,\,2)$![]() to the first equation of system (PTT), we obtain the equation that
to the first equation of system (PTT), we obtain the equation that
Taking the $L^2$![]() inner product with ${|\nabla |^{-1}} \nabla ^k \mathbb {P}\mathop {\rm div}\nolimits \tau$
inner product with ${|\nabla |^{-1}} \nabla ^k \mathbb {P}\mathop {\rm div}\nolimits \tau$![]() , and summing up $k$
, and summing up $k$![]() from $0$
from $0$![]() to $2$
to $2$![]() , we find that
, we find that

In order to deal with $J_1$![]() , we turn the time derivative of $u$
, we turn the time derivative of $u$![]() to $\tau$
to $\tau$![]() . Hence, we can transform the time derivative to the spatial derivative, i.e.
. Hence, we can transform the time derivative to the spatial derivative, i.e.

Applying the operator ${|\nabla |^{-1}}\nabla ^k \mathbb {P}\mathop {\rm div}\nolimits$![]() $(k=0,\,1,\,2)$
$(k=0,\,1,\,2)$![]() to the second equation of system (PTT), we see that
to the second equation of system (PTT), we see that

Now, using the facts that $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , we have
, we have

Here, we can deal with the remaining two terms $J_2$![]() and $J_3$
and $J_3$![]() as follows:
as follows:

Substituting the above estimates of $J_1$![]() , $J_2$
, $J_2$![]() and $J_3$
and $J_3$![]() into (3.7), we obtain (3.5) immediately.
into (3.7), we obtain (3.5) immediately.
With the help of lemmas 3.2 and 3.3, we infer the following lemma.
Lemma 3.4 Under the assumptions of proposition 3.1, it holds that
Proof. Now, adding $({2\eta }/{(1-C\eta )})\times$![]() (3.5) to (3.2), and choosing $\eta$
(3.5) to (3.2), and choosing $\eta$![]() suitably small, one obtains that
suitably small, one obtains that

Since

then there exist two positive constants $c_1$![]() and $c_2$
and $c_2$![]() , independent of $t$
, independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , such that
, such that

provided that $\eta$![]() is suitably small. Therefore, we get (3.8) immediately.
is suitably small. Therefore, we get (3.8) immediately.
3.2 Estimate of $\mathcal {E}_2(t)$
According to the estimate of $\mathcal {E}_1(t)$![]() in § 3.1, we see that it is necessary to prove some time decay estimates as $\mathcal {E}_2(t)$
in § 3.1, we see that it is necessary to prove some time decay estimates as $\mathcal {E}_2(t)$![]() .
.
Lemma 3.5 Under the assumptions of proposition 3.1, it holds that

where $C$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , and
, and
Proof. Applying the operator $\nabla ^{k+1}$![]() $(k=0,\,1)$
$(k=0,\,1)$![]() to the first equation of system (PTT) and $\nabla ^k \mathbb {P}\mathop {\rm div}\nolimits$
to the first equation of system (PTT) and $\nabla ^k \mathbb {P}\mathop {\rm div}\nolimits$![]() $(k=0,\,1)$
$(k=0,\,1)$![]() to the second equation of system (PTT), we see that
to the second equation of system (PTT), we see that

Taking the $L^2$![]() inner product of the first equation of (3.11) with $\nabla ^{k+1} u$
inner product of the first equation of (3.11) with $\nabla ^{k+1} u$![]() and the second equation of (3.11) with $2\nabla ^k \mathbb {P}\mathop {\rm div}\nolimits \tau$
and the second equation of (3.11) with $2\nabla ^k \mathbb {P}\mathop {\rm div}\nolimits \tau$![]() , we arrive at
, we arrive at

Observe that the divergence-free and symmetry conditions, and by using integration by parts, we deduce that $K_1=0$![]() . For the second term $K_2$
. For the second term $K_2$![]() , we readily have
, we readily have
We now turn to the toughest term $K_3$![]() . By taking advantage of lemma 2.1, Hölder's inequality and Gagliardo–Nirenberg–Sobolev inequality, we can conclude that
. By taking advantage of lemma 2.1, Hölder's inequality and Gagliardo–Nirenberg–Sobolev inequality, we can conclude that

For the last term $K_4$![]() , we easily get that
, we easily get that
Combining the above estimates, we get inequality (3.9).
Next, we recover the dissipation estimate for $\mathbb {P}\mathop {\rm div}\nolimits \tau$![]() .
.
Lemma 3.6 Under the assumptions of proposition 3.1, it holds that

where $C$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() , and
, and
Proof. Applying the operator $\nabla \mathbb {P}$![]() to the first equation of system (PTT), we obtain the equation that
to the first equation of system (PTT), we obtain the equation that
Taking the $L^2$![]() inner product with $\nabla \mathbb {P}\mathop {\rm div}\nolimits \tau$
inner product with $\nabla \mathbb {P}\mathop {\rm div}\nolimits \tau$![]() , we find that
, we find that

To deal with the first term $L_1$![]() , we use integration by parts to get
, we use integration by parts to get
Applying the operator $\mathbb {P}\mathop {\rm div}\nolimits$![]() to the second equation of system (PTT) yields
to the second equation of system (PTT) yields
from which it follows that
According to lemma 2.1, we have

Next, we treat the second term $L_2$![]() and the last term $L_3$
and the last term $L_3$![]() . We infer that
. We infer that

Utilizing the above estimates in (3.15), it is easy to get (3.13).
In view of lemmas 3.5 and 3.6, we obtain the following lemma.
Lemma 3.7 Under the assumptions of proposition 3.1, it holds that
Proof. As above two lemmas, together with (3.9) and $\eta \times$![]() (3.13), using the facts that $0\leq a\leq 1$
(3.13), using the facts that $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , and choosing $\eta$
, and choosing $\eta$![]() suitably small, this ensures that
suitably small, this ensures that

Since
then we have

The key to the proof is a weighted energy estimate. By multiplying the time weight $(1+t)^{2}$![]() and integrating directly in time, we obtain that
and integrating directly in time, we obtain that

Note that in the above inequality we have used the facts that

and

Since $0\leq a\leq 1$![]() and $0\leq b\leq Ca$
and $0\leq b\leq Ca$![]() , then $\lim \nolimits _{a\rightarrow 0} ({(1-{\rm e}^{-at})}/{a})=\lim \nolimits _{a\rightarrow 0} {\rm e}^{-at}\leq 1$
, then $\lim \nolimits _{a\rightarrow 0} ({(1-{\rm e}^{-at})}/{a})=\lim \nolimits _{a\rightarrow 0} {\rm e}^{-at}\leq 1$![]() , we have
, we have

Combining the above estimates, and recalling the definition of $\mathcal {E}_2(t)$![]() , it is easy to deduce estimate (3.16).
, it is easy to deduce estimate (3.16).
3.3 Estimate of $\mathcal {E}_3(t)$
Since what we obtained above is the dissipation estimate for $\mathbb {P}\mathop {\rm div}\nolimits \tau$![]() , but rather than $\tau$
, but rather than $\tau$![]() . In order to control the nonlinear term $b({\rm tr}\,\tau )\tau$
. In order to control the nonlinear term $b({\rm tr}\,\tau )\tau$![]() , we need further and more arguments. Here, we shall make full use of the structure of system (PTT) to obtain $\|{\rm tr}\,\tau \|_{H^3}$
, we need further and more arguments. Here, we shall make full use of the structure of system (PTT) to obtain $\|{\rm tr}\,\tau \|_{H^3}$![]() decays exponentially.
decays exponentially.
Lemma 3.8 Under the assumptions of proposition 3.1, it holds that
where $C$![]() is a positive constant independent of $t$
is a positive constant independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() .
.
Proof. Applying the operator ${\rm tr}\,$![]() to the second equation of (PTT), and using the fact that $\mathop {\rm div}\nolimits u=0$
to the second equation of (PTT), and using the fact that $\mathop {\rm div}\nolimits u=0$![]() , we may write
, we may write
with the following standard estimate:

Consequently, the above inequality reads
Gronwall's lemma now provides the bound

It is then obvious that

In fact, due to $0\leq b\leq Ca$![]() , we have
, we have

Returning to (3.18), and combining the estimates above, we get (3.17) immediately.
3.4 Closure of the estimates
With the help of the estimates of $\mathcal {E}_{i}(t)$![]() $(i=1,\,2,\,3)$
$(i=1,\,2,\,3)$![]() , we start to prove proposition 3.1.
, we start to prove proposition 3.1.
Proof of proposition 3.1. Together with all the estimates of $\mathcal {E}_{i}(t)$![]() $(i=1,\,2,\,3)$
$(i=1,\,2,\,3)$![]() , this gives that
, this gives that

Using the bootstrap assumption (3.1), we then get

Hence,
provided that $\delta _0$![]() is sufficiently small. This completes the proof of proposition 3.1.
is sufficiently small. This completes the proof of proposition 3.1.
4. Proofs of main results
Thus far, we have established the uniform estimates for smooth solutions with respect to $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() . In this section, we pay attention to the proofs of theorems 1.1, 1.7 and 1.8. Indeed, proposition 3.1 in § 3 leads us to prove theorem 1.1.
. In this section, we pay attention to the proofs of theorems 1.1, 1.7 and 1.8. Indeed, proposition 3.1 in § 3 leads us to prove theorem 1.1.
Proof of theorem 1.1 In contrast to the Oldroyd-B system, however, there is no derivative in the additional term $b({\rm tr}\,\tau )\tau$![]() of system (PTT). The proof of local well-posedness for system (PTT) is similar to that of the Oldroyd-B system, and will thus be omitted. Then there exists a positive time $T$
of system (PTT). The proof of local well-posedness for system (PTT) is similar to that of the Oldroyd-B system, and will thus be omitted. Then there exists a positive time $T$![]() such that, for any $0\leq t\leq T$
such that, for any $0\leq t\leq T$![]() , we have
, we have
Let $T^*$![]() denote the maximal time of existence of solutions with (4.1) holds true. We claim that $T^*=+\infty$
denote the maximal time of existence of solutions with (4.1) holds true. We claim that $T^*=+\infty$![]() . Thanks to proposition 3.1, we have
. Thanks to proposition 3.1, we have
A standard continuous argument leads to $T^*=+\infty$![]() , which completes the proof of theorem 1.1.
, which completes the proof of theorem 1.1.
Next, we employ once again proposition 3.1, combined with Aubin–Lions lemma (see lemma 2.2), to complete the proof of theorem 1.7.
Proof of theorem 1.7 For any $T>0$![]() , let $(u,\,\tau )$
, let $(u,\,\tau )$![]() be a solution of system (PTT) in the time interval $[0,\,T]$
be a solution of system (PTT) in the time interval $[0,\,T]$![]() with the initial data $({|\nabla |^{-1}} u_0,\,{|\nabla |^{-1}}\tau _0)$
with the initial data $({|\nabla |^{-1}} u_0,\,{|\nabla |^{-1}}\tau _0)$![]() belongs to $H^3$
belongs to $H^3$![]() . We immediately deduce from proposition 3.1 that the following uniform estimates:
. We immediately deduce from proposition 3.1 that the following uniform estimates:

Furthermore, being able to use the structure of system (PTT), we get
The application of the above uniform estimates and lemma 2.2 implies that there exists a subsequence still denoted by $(u,\,\tau )$![]() such that for $0\leq b\leq Ca$
such that for $0\leq b\leq Ca$![]() , when $(a,\,b)$
, when $(a,\,b)$![]() goes to $(0,\,0)$
goes to $(0,\,0)$![]() , then
, then

with $s\in (0,\,1/2)$![]() , and
, and

This allows us to pass to the limit in system (PTT) with $0\leq b\leq Ca$![]() when $(a,\,b)$
when $(a,\,b)$![]() goes to $(0,\,0)$
goes to $(0,\,0)$![]() and to conclude that the limit $(\widetilde {u},\,\widetilde {\tau })$
and to conclude that the limit $(\widetilde {u},\,\widetilde {\tau })$![]() is indeed a solution of system (OB). This completes the proof of theorem 1.7.
is indeed a solution of system (OB). This completes the proof of theorem 1.7.
Finally, we use energy estimate again to show the rate of convergence for any positive time.
Proof of theorem 1.8 Let $(u,\,\tau )$![]() and $(\widetilde {u},\,\widetilde {\tau })$
and $(\widetilde {u},\,\widetilde {\tau })$![]() be two solutions of system (PTT) and system (OB) with the same initial data, respectively. Indeed, according to theorem 1.1, we have, for any $t\geq 0$
be two solutions of system (PTT) and system (OB) with the same initial data, respectively. Indeed, according to theorem 1.1, we have, for any $t\geq 0$![]() ,
,

and
Define
We shall focus on the rate of convergence of $(u,\,\tau )$![]() towards $(\widetilde {u},\,\widetilde {\tau })$
towards $(\widetilde {u},\,\widetilde {\tau })$![]() in $H^1$
in $H^1$![]() norm. To prove this, we write the evolution equation for $(v,\,\sigma )$
norm. To prove this, we write the evolution equation for $(v,\,\sigma )$![]() that
that

Taking the $L^2$![]() inner product of the first equation of system (4.5) with $v$
inner product of the first equation of system (4.5) with $v$![]() and the second equation of system (4.5) with $\sigma$
and the second equation of system (4.5) with $\sigma$![]() , because of $\mathop {\rm div}\nolimits v=0$
, because of $\mathop {\rm div}\nolimits v=0$![]() and $\sigma _{ij}=\sigma _{ji}$
and $\sigma _{ij}=\sigma _{ji}$![]() , we get
, we get

Using the energy estimates (4.3) and (4.4), we have

Together with the above estimates, this enables us to conclude that

Similar arguments lead to

Taking advantage of the energy estimates (4.3) and (4.4), we infer that

Hence, the above estimates yield

Together (4.6) with (4.7), this implies that

As we have

then Gronwall's lemma thus leads to
for some positive constant $C$![]() , independent of $t$
, independent of $t$![]() , $a$
, $a$![]() and $b$
and $b$![]() . This completes the proof of theorem 1.8.
. This completes the proof of theorem 1.8.
Acknowledgements
Yuhui Chen is supported by NNSF of China (Grant No. 12201655) and Guangdong Basic and Applied Basic Research Foundation (Grant No. 2023A1515010974). Qinghe Yao is supported by NNSF of China (Grant No. 11972384) and Guangdong Science and Technology Fund (Grant No. 2021B1515310001). Zheng-an Yao is supported by NNSF of China (Grant No. 11971496) and National Key R&D Program of China (Grant No. 2020YFA0712500).