Research Article
Metrization of spaces having Čech dimension zero
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 161-168
-
- Article
-
- You have access
- Export citation
Relative annihilators in semilattices
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 169-185
-
- Article
-
- You have access
- Export citation
Helgason's number and lacunarity constants
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 187-218
-
- Article
-
- You have access
- Export citation
Differential equations in Banach spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 219-226
-
- Article
-
- You have access
- Export citation
On a random solution of a nonlinear perturbed stochastic integral equation of the Volterra type
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 227-237
-
- Article
-
- You have access
- Export citation
On saturated formations whose projectors are complemented
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 239-248
-
- Article
-
- You have access
- Export citation
On the complex complementarity problem
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 249-257
-
- Article
-
- You have access
- Export citation
Connected expansions of topologies
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 259-265
-
- Article
-
- You have access
- Export citation
Finite groups which are the product of two nilpotent subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 267-274
-
- Article
-
- You have access
- Export citation
On rings with trivial torsion parts
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 275-290
-
- Article
-
- You have access
- Export citation
A converse of Bernstein's inequality for locally compact groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 291-298
-
- Article
-
- You have access
- Export citation
Abstracts of Australasian PhD Theses
A discrete analytic theory of geometric difference functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 299-300
-
- Article
-
- You have access
- Export citation
Minimal number of generators of some classes of groups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 301-302
-
- Article
-
- You have access
- Export citation
Orthogonal transformations and improperly posed problems
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 303-304
-
- Article
-
- You have access
- Export citation
Two topics in the differential calculus on topological linear spaces
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 305-306
-
- Article
-
- You have access
- Export citation
Soluble groups satisfying the minimal condition for normal subgroups
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 307-308
-
- Article
-
- You have access
- Export citation
Studies in surface physics
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 309-310
-
- Article
-
- You have access
- Export citation
Topics in population genetics
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 311
-
- Article
-
- You have access
- Export citation
Microturbulent magnetoactive plasmas and polarized radiation from the solar corona
-
- Published online by Cambridge University Press:
- 17 April 2009, p. 312
-
- Article
-
- You have access
- Export citation
Semigroups of differentiable functions
-
- Published online by Cambridge University Press:
- 17 April 2009, pp. 313-314
-
- Article
-
- You have access
- Export citation



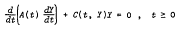

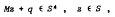
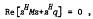
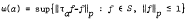
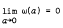 , then
, then 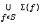 is relatively compact (where Σ(
is relatively compact (where Σ(